Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g(x) = |f(x) – m + 2018| có 7 điểm

Vietjack.me giới thiệu bộ câu hỏi ôn tập Toán có đáp án được biên soạn bám sát chương trình học giúp bạn ôn luyện và bổ sung kiến thức môn Toán tốt hơn. Mời các bạn đón xem:

1 471 02/02/2024

Trang trước

Trang sau

Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g(x) = |f(x) – m + 2018| có 7 điểm

Đề bài: Cho hàm số y = f(x) có đồ thị như hình vẽ bên dưới.

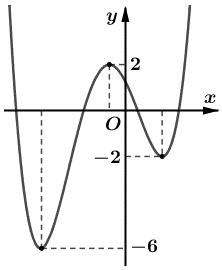
Tài liệu VietJack

Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g(x) = |f(x) – m + 2018| có 7 điểm cực trị?

Lời giải:

Quan sát đồ thị, ta thấy hàm số y = f(x) có 3 điểm cực trị.

Do đó để hàm số y = |f(x) – m + 2018| có 7 điểm cực trị thì đồ thị hàm số y = f(x) cắt đường thẳng y = m – 2018 tại 7 – 3 = 4 điểm phân biệt khác 3 điểm cực trị của hàm số y = f(x).

⇔ –2 < m – 2018 < 2.

⇔ 2016 < m < 2020.

Mà m ∈ ℤ.

Suy ra m ∈ {2017; 2018; 2019}.

Vậy có 3 giá trị nguyên dương của m thỏa mãn yêu cầu bài toán.

Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:

Cho hàm số f(x) = mx + m – 1. Tìm tất cả các giá trị thực của tham số m để phương trình...

Một cửa hàng giảm giá 10% so với giá bán bình thường nhưng vẫn lãi 8% so với giá vốn...

Tìm x, y ∈ ℤ, biết: (5x + 1)(y – 1) = 4...

Thực hiện phép tính: C = (x – 2)(x^2 + 2x + 4) – x^2(x + 2...

Cách xác định cạnh kề, cạnh đối, cạnh huyền trong tam giác vuông...

Viết phương trình đường thẳng biết đồ thị của nó cắt trục tung tại điểm có tung độ bằng 4 và...

Cho hàm số y = (m – 1)x + m (1) (với m là tham số, m ≠ 0...

Tìm dư trong phép chia đa thức f(x) = 1 + x^2 + x^4 + x^6 + ... + x^100 cho x + 1...

Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g(x) = |f(x) – m + 2018| có 7 điểm...

Cho tam giác ABC và đường trung tuyến AM. Chứng minh SAMB = SAMC...

Từ các chữ số 0; 1; 2; 3; 4; 5; 6, có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số khác...

Hình chữ nhật có nửa chu vi là 99 m. Nếu tăng chiều rộng thêm 5 m và giảm chiều dài...

Hai người xài youtube mất 2 phút để đăng 2 đoạn video. Vậy cần bao nhiêu người để...

Biết đồ thị hàm số y = ax + 5 đi qua điểm M(2; –3) thì hệ số góc bằng bao nhiêu...

Đồ thị hàm số y = –5x không đi qua điểm...

Một mảnh đất hình chữ nhật có chiều dài là 36 m, chiều rộng bằng...

Tìm số nguyên x, y, biết: (x – 3)(y + 1) = 15...

Tìm số giao điểm của parabol y = –x^2 – 3x – 1 và đường thẳng y = x + 3...

Cho hai số, biết số bé bằng 9/11 số lớn và nếu lấy số lớn trừ đi số bé và cộng với hiệu...

Cho hàm số y = ax^2 + bx + c có đồ thị như hình vẽ bên...

Cho hàm số y = ax^2 + bx + c có đồ thị như hình bên...

Với các chữ số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số gồm 8 chữ số, trong đó...

Có bao nhiêu cách sắp xếp 3 nữ sinh, 3 nam sinh thành một hàng dọc sao cho các bạn...

Diện tích hình tam giác là 25,3 cm2, chiều cao là 5,5 cm. Tính độ dài đáy của hình...

Tìm số có 3 chữ số abc sao cho abc / (a + b + c)...

Tìm số tự nhiên a, b biết ƯCLN(a, b) = 4 và a + b = 48...

Cho đường thẳng d: y = 2x + 6 cắt Ox; Oy theo thứ tự A và B. Diện tích tam giác OAB là...

Số nào khác tính chất với các số còn lại: 9678, 4572, 5261, 5133, 3527, 6895, 7768...

Một khu vườn hình chữ nhật có diện tích 3600 m² chiều rộng 40 m, cửa ra vào của...

Cho một hình chữ nhật và một hình thoi (như hình vẽ), đường chéo EK và FH của...

Trong các hình sau : hình vuông, hình bình hành, hình chữ nhật; hình thang cân...

Tính diện tích tam giác vuông cân biết cạnh huyền 4 cm...

Tìm số nguyên x, biết: (–14 ) + x – 7 = –10...

Tìm x biết x^2 + 2 là bội của x + 2...

55 + 56 + 57 + 58 – 35 – 36 – 37 – 38...

Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi I là trung điểm của AB...

Cho tứ diện ABCD. Gọi P, Q lần lượt là trung điểm của AB, CD. Điểm R nằm trên cạnh...

Một người gửi ngân hàng 100 triệu đồng với kỳ hạn 3 tháng, lãi suất 2% một quý theo...

Từ các chữ số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi...

Chứng minh rằng n^7 – n chia hết cho 7, với mọi n là số nguyên...

Hỏi có bao nhiêu cách chọn ra hai số khác nhau trong các số tự nhiên từ 1 đến 20 sao...

Trên mặt phẳng tọa độ Oxy cho A(1; –1), B(2; 1) và C(4; 5). Ba điểm A, B, C có...

Một tam giác có chu vi bằng 36 cm cạnh của nó tỉ lệ với 3; 4; 5. Tính độ dài ba cạnh...

1 471 02/02/2024

Trang trước

Trang sau

Xem thêm các chương trình khác: