Lớp 10A có 10 học sinh giỏi Toán, 10 học sinh giỏi Lý, 11 học sinh giỏi Hoá, 6 học sinh

Vietjack.me giới thiệu bộ câu hỏi ôn tập Toán có đáp án được biên soạn bám sát chương trình học giúp bạn ôn luyện và bổ sung kiến thức môn Toán tốt hơn. Mời các bạn đón xem:

1 556 13/10/2024

Trang trước

Trang sau

Lớp 10A có 10 học sinh giỏi Toán, 10 học sinh giỏi Lý, 11 học sinh giỏi Hoá, 6 học sinh

Đề bài: Lớp 10A có 10 học sinh giỏi Toán, 10 học sinh giỏi Lý, 11 học sinh giỏi Hoá, 6 học sinh giỏi Toán và Lý, 5 học sinh giỏi Hoá và Lý, 4 học sinh giỏi Toán và Hoá, 3 học sinh giỏi cà 3 môn. Hỏi số học sinh giỏi ít nhất 1 môn trong 3 môn là bao nhiêu em?

*Phương pháp giải

- vẽ biểu đồ Ven ra để nhìn cho rõ những số học sinh giỏi cả 2 môn và 3 môn

- Từ đó để tính được số học sinh giỏi chỉ 2 môn. TT để tìm ra số học sinh chỉ giỏi ít nhất 1 trong 3 môn

*Lời giải

Theo giả thiết đề bài cho, ta có biểu đồ Ven:

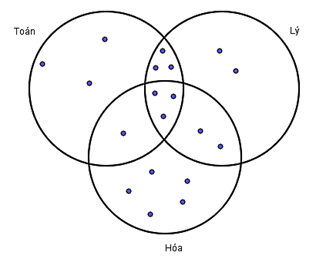
Tài liệu VietJack

Dựa vào biểu đồ Ven ta thấy:

Số học sinh chỉ giỏi Toán và Lý (không giỏi Hóa) là:

6 – 3 = 3 (em)

Số học sinh chỉ giỏi Toán và Hóa (không giỏi Lý) là:

4 – 3 = 1 (em)

Số học sinh chỉ giỏi Lý và Hóa (không giỏi Toán) là:

5 – 3 = 2 (em)

Số học sinh chỉ giỏi một môn Toán là:

10 – 3 – 3 – 1 = 3 (em)

Số học sinh chỉ giỏi một môn Lý là:

10 – 3 – 3 – 2 = 2 (em)

Số học sinh chỉ giỏi một môn Hóa là:

11 – 1 – 3 – 2 = 5 (em)

Số học sinh giỏi ít nhất một trong ba môn là:

3 + 2 + 5 + 1 + 2 + 3 + 3 =19 (em)

Đáp số: 19 em

* Phương pháp giải toán sử dụng biểu đồ Ven:

+ Bước 1: Chuyển bài toán về ngôn ngữ tập hợp.

+ Bước 2: Sử dụng sơ đồ Ven để minh họa các tập hợp.

Vẽ các vòng kín đại diện các tập hợp (mỗi vòng kín là một tập hợp), lưu ý hai vòng kín có phần chung nếu mỗi vòng kín có ít nhất một phần nằm trong vòng kín kia và hai tập hợp đó khác rỗng.

+ Bước 3: Dựa vào sơ đồ Ven ta thiết lập được đẳng thức hoặc phương trình, hệ phương trình, từ đó tìm được kết quả bài toán.

Lưu ý:

+ Nếu A và B là hai tập hợp hữu hạn thì n(A ∪ B) = n(A) + n(B) – n(A ∩ B).

⇒ n(A ∩ B) = n(A) + n(B) – n(A ∪ B).

+ Nếu A và B không có phần tử chung, tức là A ∩ B = ∅, thì n(A ∪ B) = n(A) + n(B).

Xem thêm các bài viết liên quan hay chi tiết:

Lý thuyết Tập hợp và các phép toán trên tập hợp - Toán 10 Kết nối tri thức

Giải SBT Toán 10 Bài 2. Tập hợp và các phép toán trên tập hợp có đáp án

Trắc nghiệm Toán 10 CTST Bài 3: Các phép toán trên tập hợp có đáp án

Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:

Xác định a, b, c biết parabol y = ax2 + bx + c đi qua điểm A(8; 0) và có đỉnh là I(6; −12...

Biết giá bán 1 kg cam cao hơn 10% so với giá 1 kg xoài. Hỏi giá 1 kg xoài thấp hơn giá...