Giải SBT Toán 10 Bài 2. Tập hợp và các phép toán trên tập hợp có đáp án
Giải SBT Toán 10 Bài 2. Tập hợp và các phép toán trên tập hợp có đáp án
-
148 lượt thi
-
15 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
17/07/2024Điền Đ vào ô trống nếu mệnh đề đúng, điền S vào ô trống nếu mệnh đề sai.
a) ∅ ⊂ ℕ  ;
;
b) ℕ ⊂ ℚ  ;
;
c) ∅ = {0}  ;
;
d) {∅} ⊂ ℝ  .
.
 Xem đáp án
Xem đáp án
Lời giải:
a) Tập rỗng là tập con của mọi tập hợp nên ∅ ⊂ ℕ 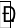
b) Các số tự nhiên có thể biểu diễn thành các số hữu tỉ với mẫu số bằng 1.
Do đó ℕ ⊂ ℚ 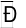 ;
;
c) Tập rỗng là tập hợp không có phần tử, tập {0} có một phần tử là 0 nên ∅ = {0} 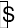
d) Không có tập hợp chỉ chứa tập rỗng do đó {∅} ⊂ ℝ 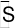 .
.
Câu 2:
17/07/2024Cho hai tập hợp A, B được mô tả bởi biểu đồ Ven như sau:
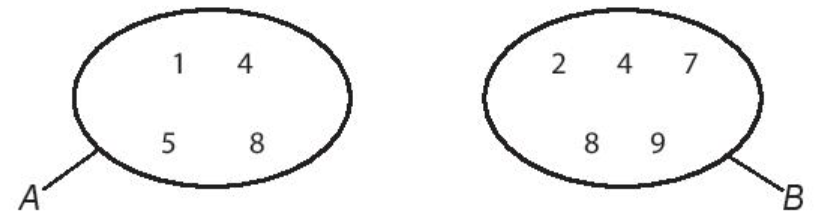
Hãy chỉ ra các phần tử của tập hợp A, tập hợp B.
 Xem đáp án
Xem đáp án
Lời giải:
Ta có:
A = {1; 4; 5; 8}.
B = {2; 4; 7; 8; 9}.
Câu 3:
19/07/2024Cho hai tập hợp A, B được mô tả bởi biểu đồ Ven như sau:

Tính n(A ∪ B).
 Xem đáp án
Xem đáp án
Lời giải:
Ta có A ∪ B = {1; 2; 4; 5; 7; 8; 9} nên n(A ∪ B) = 7.
Câu 4:
15/07/2024Cho hai tập hợp A, B được mô tả bởi biểu đồ Ven như sau:

Hãy chỉ ra các phần tử thuộc tập hợp A mà không thuộc tập hợp B.
 Xem đáp án
Xem đáp án
Lời giải:
Các phần tử thuộc tập hợp A mà không thuộc tập hợp B là: 1; 5.
Do đó A \ B = {1; 5}.
Câu 5:
25/06/2024Cho hai tập hợp A, B được mô tả bởi biểu đồ Ven như sau:

Hãy chỉ ra các phần tử thuộc tập hợp B mà không thuộc tập hợp A.
 Xem đáp án
Xem đáp án
Lời giải:
Các phần tử thuộc tập hợp B mà không thuộc tập hợp A là: 2; 7; 9.
Do đó B \ A = {2; 7; 9}.
Câu 6:
22/07/2024Xác định các tập hợp sau bằng cách nêu tính chất đặc trưng cho phần tử của tập hợp.
A = {0; 4; 8; 12; 16}; B = {3; 9; 27; 81}; C là đường thẳng trung trực của đoạn thẳng AB.
 Xem đáp án
Xem đáp án
Lời giải:
Xét tập A = {0; 4; 8; 12; 16}
Ta thấy các phần tử của tập A là các số tự nhiên chia hết cho 4, nhỏ nhất là 0 và lớn nhất là 16.
Do đó A = {4x | x ℕ; x ≤ 4}.
Xét tập B = {3; 9; 27; 81}
Ta thấy 3 = (3)1; 9 = (3)2; 27 = (3)3; 81 = (3)4.
Do đó các phần tử của tập B là các lũy thừa của 3 với số mũ tăng dần từ 1 đến 4.
Do đó B = {(3)x | x ℕ; 1 ≤ x ≤ 4}.
Xét tập C là đường thẳng trung trực của đoạn thẳng AB.
Các điểm nằm trên đường trung trực của đoạn thẳng AB thì cách đều hai đầu mút A và B.
Do đó C = {P | PA = PB}.
Câu 7:
20/07/2024Trong các tập hợp sau, tập nào là tập rỗng?
A = {x ℕ | x ≤ 0}; B = {x ℕ | 2x2 3x 5 = 0}.
 Xem đáp án
Xem đáp án
Lời giải:
Xét tập A = {x ℕ | x ≤ 0}
Ta thấy x ℕ mà x ≤ 0 nên x = 0.
Do đó tập A có một phần tử là 0 nên tập A không phải là tập rỗng.
Xét tập B = {x ℕ | 2x2 3x 5 = 0}
Ta có 2x2 3x 5 = 0
2x2 + 2x 5x 5 = 0
2x(x + 1) 5(x + 1) = 0
(x + 1)(2x 5) = 0



Ta thấy 1 là một số nguyên âm,  là một số hữu tỉ, cả hai số này đều không phải số tự nhiên nên không có số tự nhiên x thỏa mãn 2x2 3x 5 = 0.
là một số hữu tỉ, cả hai số này đều không phải số tự nhiên nên không có số tự nhiên x thỏa mãn 2x2 3x 5 = 0.
Do đó tập B là tập rỗng.
Câu 8:
21/07/2024Trong các mệnh đề sau, mệnh đề nào đúng? Mệnh đề nào sai? Giải thích kết luận đưa ra.
a) Tập rỗng là tập con của mọi tập hợp;
b) Nếu X = {a; b} thì a X;
c) Nếu X = {a; b} thì {a; b} X.
 Xem đáp án
Xem đáp án
Lời giải:
a) Theo quy ước ta có tập rỗng là tập con của mọi tập hợp nên mệnh đề “Tập rỗng là tập con của mọi tập hợp” là mệnh đề đúng.
b) Nếu X = {a; b} thì phần tử a thuộc tập hợp X.
Do đó mệnh đề “Nếu X = {a; b} thì a X” là mệnh đề sai.
c) Một tập hợp là tập con của chính tập hợp đó.
Do đó mệnh đề “Nếu X = {a; b} thì {a; b} X” là mệnh đề đúng.
Câu 9:
21/07/2024Xác định các tập hợp sau và biểu diễn chúng trên trục số.
(4; 7) ∩ (1; 3);
 Xem đáp án
Xem đáp án
Lời giải:
(4; 7) ∩ (1; 3) = ∅.
Do đó ta không biểu diễn được tập hợp (4; 7) ∩ (1; 3) trên trục số.
Câu 10:
15/07/2024Xác định các tập hợp sau và biểu diễn chúng trên trục số.
(2; 1] ∩ (; 1);
 Xem đáp án
Xem đáp án
Lời giải:
(2; 1] ∩ (; 1) = (2; 1).
Ta có hình biểu diễn tập hợp (2; 1) trên trục số như sau:

Câu 11:
09/07/2024Xác định các tập hợp sau và biểu diễn chúng trên trục số.
(2; 6) \ (3; 10);
 Xem đáp án
Xem đáp án
Lời giải:
(2; 6) \ (3; 10) = (2; 3] ∪ (3; 6) \ (3; 10) = (2; 3].
Ta có hình biểu diễn tập hợp (2; 3] trên trục số như sau:

Câu 12:
12/07/2024Xác định các tập hợp sau và biểu diễn chúng trên trục số.
(3; 5] \ [2; 8).
 Xem đáp án
Xem đáp án
Lời giải:
(3; 5] \ [2; 8) = (3; 2) ∪ [2; 5] \ [2; 8) = (3; 2).
Ta có hình biểu diễn tập hợp (3; 2) trên trục số như sau:

Câu 13:
20/07/2024Trong một cuộc phỏng vấn 56 người về những việc họ thường làm vào ngày nghỉ cuối tuần, có 24 người thích tập thể thao, 15 người thích đi câu cá và 20 người không thích cả hai hoạt động trên.
Có bao nhiêu người thích chơi thể thao hoặc thích câu cá?
c) Có bao nhiêu người chỉ thích câu cá, không thích chơi thể thao?
 Xem đáp án
Xem đáp án
Lời giải:
Trong số 56 người phỏng vấn, có 20 người không thích cả hai hoạt động nên số người hoặc thích chơi thể thao hoặc thích câu cá là:
56 – 20 = 36 (người)
Vậy có 36 người thích chơi thể thao hoặc thích câu cá.
Câu 14:
22/07/2024Trong một cuộc phỏng vấn 56 người về những việc họ thường làm vào ngày nghỉ cuối tuần, có 24 người thích tập thể thao, 15 người thích đi câu cá và 20 người không thích cả hai hoạt động trên.
Có bao nhiêu người thích cả câu cá và chơi thể thao?
 Xem đáp án
Xem đáp án
Lời giải:
Trong số 56 người phỏng vấn, có 24 người thích tập thể thao, 15 người thích đi câu cá nên số người thích cả câu cá và chơi thể thao là:
24 + 15 36 = 3 (người).
Vậy có 3 người thích cả câu cá và chơi thể thao.
Câu 15:
22/07/2024Trong một cuộc phỏng vấn 56 người về những việc họ thường làm vào ngày nghỉ cuối tuần, có 24 người thích tập thể thao, 15 người thích đi câu cá và 20 người không thích cả hai hoạt động trên.
Có bao nhiêu người chỉ thích câu cá, không thích chơi thể thao?
 Xem đáp án
Xem đáp án
Lời giải:
Trong 15 người thích câu cá thì có 3 người thích thêm cả hoạt động thể thao nên số người chỉ thích câu cá, không thích chơi thể thao là:
15 3 = 12 (người).
Vậy có 12 người chỉ thích câu cá, không thích chơi thể thao.
