Nội dung bài viết

    Xem thêm

    Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC: a) Chứng minh: AB bình + CH bình

    Vietjack.me giới thiệu bộ câu hỏi ôn tập Toán có đáp án được biên soạn bám sát chương trình học giúp bạn ôn luyện và bổ sung kiến thức môn Toán tốt hơn. Mời các bạn đón xem:

    1 359 28/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    15000 câu hỏi ôn tập Toán (Phần 104)

    Đề bài. Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC:

    a) Chứng minh: AB2 + CH2 = AC2 + BH2.

    b) Trên AB lấy E, trên AC lấy điểm F. Chứng minh: EF < BC.

    c) Biết AB = 6cm; AC = 8cm. Tính AH, BH, CH.

    Lời giải:

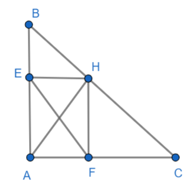    a) Áp dụng định lý Pytago vào tam giác AHB, AHC vuông có:

    AB2 = BH2 + AH2 ⇒ AH2 = AB2 – BH2

    AH2 = AC2 – CH2

    Suy ra: AB2 – BH2 = AC2 – CH2

    Hay AB2 + CH2 = AC2 + BH2

    b) Ta có: EF2 = AE2 + AF2

    BC2 = AB2 + AC2

    AE < AB, AF < AC

    Suy ra: EF2 < BC2

    ⇒ EF < BC.

    c) B⁢C=A⁢B2+A⁢C2 =10⁢(c⁢m)

    A⁢H.B⁢C=A⁢B.A⁢C⇒A⁢H=A⁢B.A⁢CB⁢C=6.810=4,8⁢(c⁢m)

    Mà AH2 = AC2 – CH2

    Nên: CH = A⁢C2-A⁢H2=6,4⁢(c⁢m)

    BH = BC – CH = 10 – 6,4 = 3,6(cm).

    *Phương pháp giải:

    Sử dụng định lí pyta go

    *Lý thuyết:

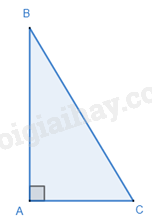
    1. Định lí Pythagore

    Trong một tam giác vuông, bình phương độ dài của cạnh huyền bằng tổng các bình phương độ dài của hai cạnh góc vuông.

    ΔABC,A^=90o⇒BC2=AB2+AC2

    (ảnh 1)

    2. Định lí Pythagore đảo

    Nếu một tam giác có bình phương độ dài của một cạnh bằng tổng các bình phương độ dài của hai cạnh kia thì tam giác đó là tam giác vuông.

    (ảnh 2)

    ΔABC,BC2=AB2+AC2⇒A^=90o

    Xem thêm

    Lý thuyết Định lí Pythagore – Toán lớp 8 Chân trời sáng tạo

     Xem thêm các bài giải bộ 15000 câu hỏi Toán hay và chi tiết tại:

    Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho vecto BH =1/3 HC...

    Cho tam giác ABC có góc A = 70 độ, các đường phân giác BD, CE cắt nhau ở I...

    Cho tam giác ABC có góc C = 90 độ. Kẻ đường cao CH. Biết HB - HA = AC...

    Cho tam giác ABC có góc C nhọn, AH và BK là hai đường cao, HK = căn 7...

    Cho tam giác ABC cân. Gọi M là trung điểm của đường cao AH, D là giao điểm của AB và CM...

    Cho tam giác ABC, D là trung điểm AB, E là trung điểm AC. Vẽ F sao cho E là trung điểm DF...

    Cho tam giác đều ABC cạnh 2a, G là trọng tâm. Khi đó độ dài vecto AB - vecto GC bằng...

    Tam giác ABC đều cạnh a, dựng hình vuông BCMN. Gọi G là trọng tâm tam giác ABC. Tính theo a độ dài vectơ u...

    Cho tam giác ABC đều cạnh a, AH là đường cao. Tính: vecto CB . vecto BA...

    Cho tam giác ABC đều cạnh a, đường cao AH. Tính độ dài vecto u...

    Cho tam giác đều ABC cạnh a, gọi G là trọng tâm. Khi đó giá trị vecto AB - vecto GC...

    Cho tam giác ABC đều có cạnh bằng a căn 3. Gọi M là trung điểm của AC...

    Cho tam giác ABC, điểm D đối xứng vs A qua B, E đối xứng B qua C, F đối xứng C qua A...

    Cho tam giác ABC, đường trung tuyến AD. Gọi M là một điểm trên cạnh AC sao cho AM = 1/2 MC...

    Cho tam giác ABC. Chứng minh rằng nếu vecto GA + vecto GB + vecto GC = vecto 0...

    Cho tam giác ABC, M là trung điểm của BC và MA = MB = MC. Chứng minh tam giác ABC là tam giác vuông...

    Cho tam giác ABC nhọn (AB < AC ) có ba đường cao AD, BE, CF cắt nhau tại H...

    Cho tam giác ABC nhọn (AB < AC) có các đường cao BD và CE. a, Cho góc A = 60 độ và AC = 12cm...

    Cho tam giác ABC nhọn, đường cao AH. M, N là hình chiếu vuông góc của H lên AB và AC...

    Cho tam giác ABC nhọn có đường cao AH. Gọi E là hình chiếu của H trên AB. a. Biết AE = 3,6 cm; BE = 6,4 cm...

    Tham khảo các loạt bài Toán khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 359 28/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: