Trắc nghiệm Định lý Py - ta - go có đáp án - Toán lớp 7
Bộ 21 bài tập trắc nghiệm Toán lớp 7 Bài 7: Định lý Py - ta - go có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 7 Bài 7.
Trắc nghiệm Toán 7 Bài 7: Định lý Py - ta - go
Bài giảng Trắc nghiệm Toán 7 Bài 7: Định lý Py - ta - go
Câu 1: Cho tam giác ABC vuông ở A có AC=20cmAC=20cm. Kẻ AH vuông góc BC. Biết BH=9cmBH=9cm; HC=16cmHC=16cm. Tính AB, AH
A. AH=12cm; AB=15cmAH=12cm; AB=15cm
B. AH=10cm; AB=15cmAH=10cm; AB=15cm
C. AH=15cm; AB=12cmAH=15cm; AB=12cm
D. AH=12cm; AB=13cmAH=12cm; AB=13cm
Đáp án: A
Giải thích:
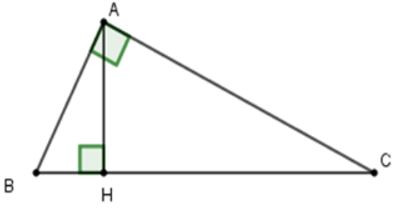
Ta có:
BC=BH+HC=9+16=25cmBC=BH+HC=9+16=25cm
Xét tam giác ABC vuông tại A, theo định lí Pytago ta có:
AB2+AC2=BC2⇒AB2+202=252⇔AB2=625-400=225⇒AB=15cm
Xét tam giác ABH vuông tại H, theo định lí Pytago ta có:
HA2+HB2=AB2⇒HA2+92=225⇒HA2=225-81=144⇒HA=12cm
Vậy AH=12cm; AB=15cm
Câu 2: Cho tam giác ABC vuông cân ở A. Tính độ dài BC biết AB=AC=2dm
A. BC=4dm
B. BC=√6dm
C. BC=8dm
D. BC=√8dm
Đáp án: D
Giải thích:
Vì tam giác ABC vuông cân tại tại A nên theo định lí Pytago có:
AB2+AC2=BC2 mà AB=AC=2dm
Nên
BC2=22+22=8⇒BC=√8(dm)
Câu 3: Một tam giác có cạnh huyền bằng 26cm độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông
A. 12 cm; 24 cm
B. 10 cm; 22 cm
C. 10 cm; 24 cm
D. 15 cm; 24 cm
Đáp án: C
Giải thích:
Gọi độ dài hai cạnh góc vuông là x; y (x; y>0)
Theo định lí Pytago ta có:
x2+y2=262⇔x2+y2=676
Theo bài ra ta có:
x5=y12⇒x225=y2144=x2+y225+144=676169=4
⇒x2=25.4=100⇒x=10cmy2=144.4=756⇒y=24cm
Vậy các cạnh góc vuông có độ dài 10 cm; 24 cm
Câu 4: Cho tam giác ABC vuông cân ở A. Tính độ dài BC biết AB=AC=4dm
A. BC=6dm
B. BC=√23dm
C. BC=4dm
D. BC=√32dm
Đáp án: D
Giải thích:
Vì tam giác ABC vuông cân tại tại A nên theo định lí Pytago có:
AB2+AC2=BC2 mà AB=AC=4dm
Nên BC2=42+42=32⇒BC=√32(dm)
Câu 5: Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau
A. 15cm; 8cm; 18cm
B. 21dm; 20dm; 29dm
C. 5m; 6m; 8m
D. 2m; 3m; 4m
Đáp án: B
Giải thích:
+ Với bộ số 15cm; 8cm; 18cm ta thấy
182=324; 152+82=289
Nên 289 < 324 hay 152+82<182
Nên loại A
+ Với bộ số 21dm; 20dm; 29dm ta thấy
292=841; 212+202=841
Nên 212+202=292 hay tam giác với độ dài 21dm; 20dm; 29dm thì tam giác đó là tam giác vuông (theo định lí Pytago đảo)
+Với bộ số 5m; 6m; 8m ta thấy
82=64; 52+62=41⇒82>52+62
Nên loại C
+ Với bộ số 2m; 3m; 4m ta thấy
42=16; 22+32=13⇒42>22+32
Nên loại D
Câu 6: Cho tam giác MNP vuông tại P khi đó:
A. MN2=MP2-NP2
B. MP2=MN2+NP2
C. NP2=MN2+MP2
D. MN2=NP2+MP2
Đáp án: D
Giải thích:
Vì Cho tam giác MNP vuông tại P nên theo định lí Pytago có:
MN2=NP2+MP2
Câu 7: Tính cạnh huyền của một tam giác biết tỉ số các cạnh góc vuông 5:12 và chu vi tam giác bằng 60 cm
A. 20 cm
B. 24 cm
C. 26 cm
D. 10 cm
Đáp án: C
Giải thích:
Gọi độ dài hai cạnh góc vuông là x; y (y>x>0)(cm) và độ dài cạnh huyền là z (z>y)(cm)
Theo đề bài ta có: x5=y12 và x+y+z=60cm
Đặt x5=y12=k(k>0) suy ra x=5k; y=12k
Theo định lí Pytago ta có:
x2+y2=z2⇒z2=(5k)2+(12k)2⇒z2=169k2=(13k)2⇒z=13k
Suy ra:
x+y+z=5k+12k+13k=30k=60⇒k=2(tm)
Từ đó: z=13k=13.2=26
Vậy cạnh huyền dài 26cm
Câu 8: Một tam giác có cạnh huyền bằng 20cm độ dài các cạnh góc vuông tỉ lệ với 3 và 4. Tính độ dài các cạnh góc vuông
A. 9 cm; 12 cm
B. 10 cm; 16 cm
C. 12 cm; 16 cm
D. 12 cm; 14 cm
Đáp án: C
Giải thích:
Gọi độ dài hai cạnh góc vuông là x; y (x; y>0)
Theo định lí Pytago ta có:
x2+y2=202⇔x2+y2=400
Theo bài ra ta có:
x3=y4⇒x29=y216=x2+y29+16=40025=16
⇒x2=16.9=144⇒x=12cmy2=16.14=256⇒y=16cm
Vậy các cạnh góc vuông có độ dài 12 cm; 16 cm
Câu 9: Cho tam giác ABC vuông tại B khi đó x=1
A. AB2+BC2=AC2
B. AB2-BC2=AC2
C. AB2+AC2=BC2
D. AB2=AC2+BC2
Đáp án: A
Giải thích:
Vì tam giác ABC vuông tại B nên theo định lí Pytago có:
AB2+BC2=AC2
Câu 10: Cho hình vẽ . Tính x
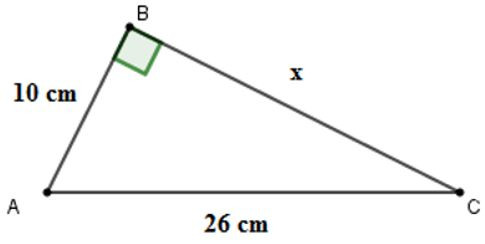
A. x = 22cm
B. x = 32cm
C. x = 20cm
D. x = 24cm
Đáp án: D
Giải thích:
Áp dụng định lí Pytago cho tam giác ABC vuông tại B ta được:
AC2=AB2+BC2⇒BC2=AC2-AB2⇒x2=262-102=576⇒x=24cm
Vậy x = 24cm
Câu 11: Cho hình vẽ . Tính x
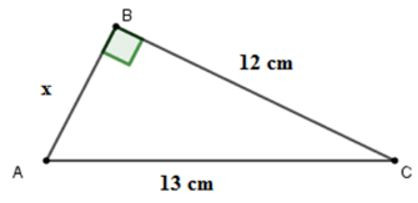
A. x = 10cm
B. x = 11cm
C. x = 8cm
D. x = 5cm
Đáp án: D
Giải thích:
Áp dụng định lí Pytago cho tam giác ABC vuông tại B ta được:
AC2=AB2+BC2⇒AB2=AC2-BC2⇒x2=132-122=25⇒x=5cm
Vậy x = 5cm
Câu 12: Tính x trong hình vẽ sau:
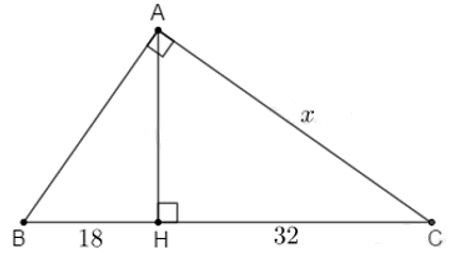
A. 36
B. 40
C. 42
D. 30
Đáp án: B
Giải thích:
Áp dụng định lí Pytago vào △ABH vuông tại H ta có:
AB2=AH2+BH2⇒AH2=AB2-BH2(1)
Áp dụng định lí Pytago vào △ACH vuông tại H ta có:
AC2=AH2+CH2⇒AH2=AC2-HC2(2)
Từ (1) và (2) ta có:
AB2-HB2=AC2-HC2⇒AB2-182=x2-322⇒AB2=x2-322+182⇒AB2=x2-1024+324⇒AB2=x2-700
Ta có: BC=BH+CH=18+32=50
Áp dụng định lí Pytago vào tam giác ABC vuông tại A ta có:
BC2=AB2+AC2⇒AB2+x2=502(3)
Thay AB2=x2-700 vào (3) ta được:
(x2-700)+x2=502⇒2x2=2500+700⇒2x2=3200⇒x2=3200:2=1600⇒x=√1600=40
Câu 13: Cho tam giác ABC, kẻ AH vuông góc BC. Tính chu vi △ABC biết AB=5cm, AH=4cm, HC=√184cm (làm tròn đến chữ số thập phân thứ nhất)
A. 30,8 cm
B. 35,7 cm
C. 31 cm
D. 31,7 cm
Đáp án: B
Giải thích:
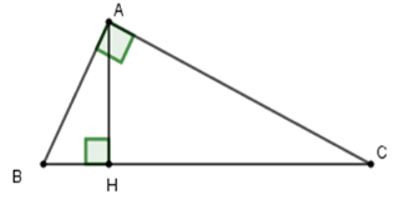
Áp dụng định lí Pytago cho tam giác ABH vuông tại H ta được:
AH2+HB2=AB2⇒HB2=AB2-AH2=52-42=9
⇒HB=3cm
Suy ra:
BC=HB+HC=3+√184cm
Áp dụng định lí Pytago cho tam giác vuông AHC ta được:
AC2=AH2+HC2=42+184=200⇒AC=√200cm
Chu vi tam giác ABC là
AB+AC+BC=5+√200+3+√184≈35,7(cm)
Câu 14: Cho tam giác ABC có ˆB; ˆC là các góc nhọn. Gọi H là chân đường vuông góc hạ từ A xuống BC. Biết AH=6cm, BH=4,5cm, HC=8cm. Khi đó △ABC là tam giác gì?
A. Tam giác cân
B. Tam giác vuông
C. Tam giác vuông cân
D. Tam giác đều
Đáp án: B
Giải thích:
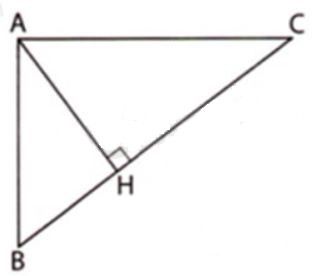
Áp dụng định lí Pytago vào △ABH vuông tại H ta có:
AB2=AH2+BH2⇒AB2=62+4,52=36+814=2254
Áp dụng định lí Pytago vào △ACH vuông tại H ta có:
AC2=AH2+CH2⇒AC2=62+82=36+64=100
Ta có: BC=BH+HC=4,5+8=252
⇒BC2=(252)2=6254(1)
Ta có:AB2+AC2=2254+100=6254(2)
Từ (1) và (2) suy ra: AB2+AC2=BC2
Vậy tam giác ABC vuông tại A
Câu 15: Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau
A. 11cm; 7cm; 8cm
B. 12dm; 15dm; 18dm
C. 9m; 12m; 15m
D. 6m; 7m; 9m
Đáp án: C
Giải thích:
+ Với bộ số 11cm; 7cm; 8cm ta thấy
112=121; 72+82=113⇒112>72+82
Nên loại A
+ Với bộ số 12dm; 15dm; 18dm ta thấy
182=324; 122+152=369⇒122+152>182
Nên loại B
+ Với bộ số 9m; 12m; 15m ta thấy
152=225; 92+122=225⇒92+122=152
Theo định lí Pytago đảo, tam giác với ba cạnh có độ dài 9m; 12m; 15m là tam giác vuông
+Vói bộ số 6m;7m;9m ta thấy
92=81; 62+72=85⇒62+72=92
Nên loại D
Câu 16: Tính x trong hình vẽ sau:
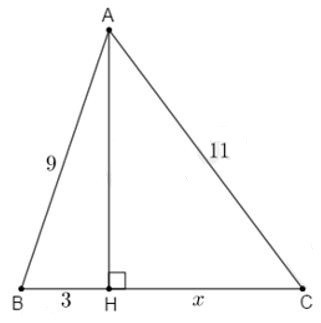
A. x = 6
B. x = 7
C. x = 8
D. x = 9
Đáp án: B
Giải thích:
Áp dụng định lí Pytago vào △ABH vuông tại H ta có:
AB2=AH2+BH2⇒AH2=AB2-BH2=92-32=72
Áp dụng định lí Pytago vào △ACH vuông tại H ta có:
AC2=AH2+CH2⇒HC2=AC2-AH2=112-72=49⇒x=HC=√49=7
Câu 17: Cho hình vẽ. Tính x
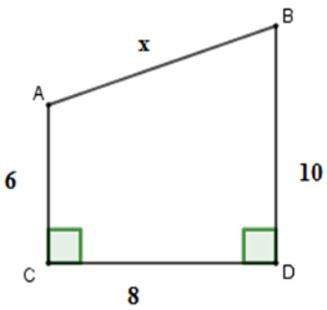
A. AB = 7
B. AB = 8
C. AB=√78
D. AB=√80
Đáp án: D
Giải thích:
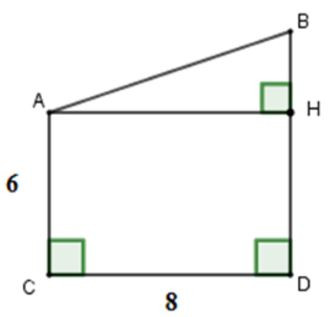
Kẻ AH⊥BD tại H
Khi đó ACDH là hình chữ nhật suy ra
HD=AC=6; AH=CD=8
Do đó: BH=BD-DH=10-6-4
Áp dụng định lí Pytago cho tam giác vuông AHB ta được:
AB2=AH2+HB2=42+82=80⇒AB=√80
Câu 18: Cho tam giác ABC, kẻ AH vuông góc BC. Tính chu vi △AHB biết
AB=15cm; AH=12cm; HC=16cm
A. 62 cm
B. 60 cm
C. 64 cm
D. 58 cm
Đáp án: B
Giải thích:
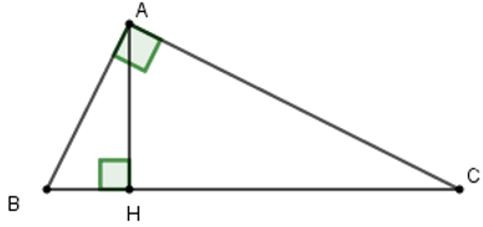
Áp dụng định lí Pytago cho tam giác ABH vuông tại H ta được:
AH2+HB2=AB2⇒HB2=AB2-AH2=152-122=81⇒HB=√81=9cm
Suy ra BC=HB+HC=9+16=25cm
Áp dụng định lí Pytago cho tam giác vuông AHC ta được:
AC2=AH2+HC2=122+62=400⇒AC=√400=20cm
Chu vi tam giác ABC là:
AB+AC+BC=15+20+25=60(cm)
Câu 19: Một tam giác có độ dào ba đường cao là 4,8 cm; 6 cm; 8 cm. Tam giác đó là tam giác gì?
A. Tam giác cân
B. Tam giác vuông
C. Tam giác vuông cân
D. Tam giác đều
Đáp án: B
Giải thích:
Gọi a,b,c lần lượt là độ dài ba cạnh của tam giác ứng với các đường cao theo thứ tự đã cho, S là diện tích △ABC (a, b, c, S>0)
Ta có: S=12.4,8A=12.6.b=12.8.c
⇒4,8a=6b=8c=2S
Do đó:
a=2S4,8=5S12b=2S6=S3c=2S8=S4
Ta có:
b2+c2=(S3)2+(S4)2=S29+S216=25S2144a2=(5S12)2=25S2144
Suy ra b2+c2=a2 nên tam giác đã cho là tam giác vuông, đỉnh góc vuông tương ứng với đường cao độ dài 4,8 cm
Câu 20: Cho ABCD là hình vuông cạnh 4cm (hình vẽ). Khi đó, độ dài đường chéo AC là
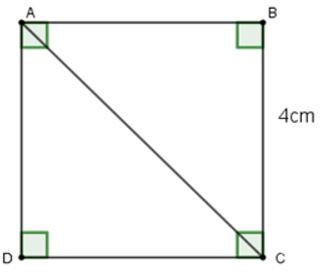
A. AC=√32cm
B. AC=5cm
C. AC=√30cm
D. AC=8cm
Đáp án: A
Giải thích:
Vì ABCD là hình vuông nên AB = BC = 4cm
Áp dụng định lí Pytago cho tam giác ABC vuông tại B ta có:
AC2=AB2+BC2=42+42=32⇒AC=√32(cm)
Câu 21: Tính cạnh huyền của một tam giác biết tỉ số các cạnh góc vuông 3:4 và chu vi tam giác bằng 36 cm
A. 9 cm
B. 12 cm
C. 15 cm
D. 16 cm
Đáp án: C
Giải thích:
Gọi độ dài hai cạnh góc vuông là x; y (y>x>0)(cm) và độ dài cạnh huyền là z (z>y)(cm)
Theo đề bài ta có: x3=y4 và x+y+z=36cm
Đặt x3=y4=k(k>0) suy ra x=3k; y=4k
Theo định lí Pytago ta có:
x2+y2=z2⇒z2=(3k)2+(4k)2=25k2=(5k)2⇒z=5k
Suy ra:
x+y+z=3k+4k+5k=12k=36⇒k=3(tm)
Từ đó: x=9cm; y=12cm; z=15cm
Vậy cạnh huyền dài 15cm
Các câu hỏi trắc nghiệm Toán lớp 7 có đáp án, chọn lọc khác:
Trắc nghiệm Trường hợp bằng nhau của hai tam giác vuông có đáp án
Trắc nghiệm Bài ôn tập chương 2 hình học có đáp án
Trắc nghiệm Quan hệ giữa góc và cạnh đối diện trong tam giác có đáp án
Trắc nghiệm Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức trong tam giác có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học 8 có đáp án
- Trắc nghiệm Toán lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn 8 có đáp án
- Trắc nghiệm Hóa học lớp 8 có đáp án
- Trắc nghiệm Địa Lí lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 8 có đáp án
- Trắc nghiệm GDCD lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Vật Lí lớp 8 có đáp án
- Trắc nghiệm Công nghệ lớp 8 có đáp án
- Trắc nghiệm Tin học lớp 8 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Sinh học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Toán lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Hóa học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn lớp 11 có đáp án
- Trắc nghiệm Tiếng Anh lớp 11 có đáp án
- Trắc nghiệm Vật Lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Địa lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm GDCD lớp 11 có đáp án
- Trắc nghiệm Lịch sử lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Công nghệ lớp 11 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 11 có đáp án
- Trắc nghiệm Tin học lớp 11 có đáp án
- Trắc nghiệm Toán lớp 12 có đáp án
- Trắc nghiệm Sinh học lớp 12 có đáp án
- Trắc nghiệm Hóa học lớp 12 có đáp án
- Trắc nghiệm Ngữ văn lớp 12 có đáp án
- Trắc nghiệm Tiếng Anh lớp 12 có đáp án
- Trắc nghiệm Địa lí lớp 12 có đáp án
- Trắc nghiệm Vật Lí lớp 12 có đáp án
- Trắc nghiệm Công nghệ lớp 12 có đáp án
- Trắc nghiệm Giáo dục công dân lớp 12 có đáp án
- Trắc nghiệm Lịch sử lớp 12 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 12 có đáp án
