Nội dung bài viết

    Xem thêm

    Trắc nghiệm Trường hợp bằng nhau của hai tam giác vuông có đáp án - Toán lớp 7

    Bộ 13 bài tập trắc nghiệm Toán lớp 7 Bài 8: Trường hợp bằng nhau của hai tam giác vuông có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 7 Bài 8.

    1 1,896 04/04/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Trắc nghiệm Toán 7 Bài 8: Trường hợp bằng nhau của hai tam giác vuông


    Bài giảng Trắc nghiệm Toán 7 Bài 8: Trường hợp bằng nhau của hai tam giác vuông

    Câu 1: Cho tam giác ABC và tam giác NPM có BC=PM; B^=P^=90°. Cần thêm một điều kiện gì để tam giác ABC và tam giác NPM bằng nhau theo trường hợp cạnh huyền - góc vuông?

    A. BA = PM

    B. BA = PN

    C. CA = MN

    D. A^=N^

    Đáp án: C

    Giải thích:

    Ta có tam giác ABC và tam giác NPM có BC=PM; B^=P^=90° mà BC; PM là hai cạnh góc vuông của hai tam giác ABC và tam giác NPM nên để hai tam giác bằng nhau theo trường hợp cạnh huyền - góc vuông thì ta cần thêm hai cạnh huyền bằng nhau là CA = MN

    Câu 2: Cho tam giác DEF và tam giác JIK có: EF=IK; D^=J^=90°. Cần thêm một điều kiện gì để △DEF=△JIK theo trường hợp cạnh huyền - góc vuông?

    A. DE = JK

    B. DF = JI

    C. DE = JI

    D. E^=I^

    Đáp án: C

    Giải thích:

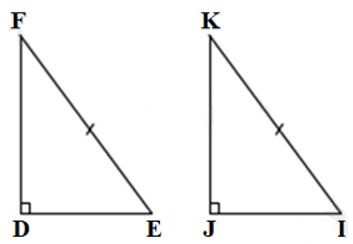
    Trắc nghiệm Trường hợp bằng nhau của hai tam giác vuông có đáp án - Toán lớp 7 (ảnh 1)

    Ta có: tam giác DEF và tam giác JIK có: EF = IK; D^=J^=90° mà EF; IK là hai cạnh huyền của hai tam giác DEF và JIK nên để △DEF=△JIK theo trường hợp cạnh huyền - góc vuông thì ta cần thêm hai cạnh góc vuông bằng nhau là DE = JI hoặc DF = JK.

    Câu 3: Cho tam giác ABC và tam giác MNP có: A^=M^=90°; C^=P^. Cần thêm một điều kiện gì để tam giác ABC và tam giác MNP theo trường hợp cạnh góc vuông - góc nhọn kề?

    A. AC = MP

    B. AB = MN

    C. BC = NP

    D. AC = MN

    Đáp án: A

    Giải thích:

    Ta có: C^=P^ mà góc C và góc P là hai góc nhọn kề của hai tam giác ABC và MNP

    Do đó: để tam giác ABC và tam giác MNP theo trường hợp cạnh góc vuông - góc nhọn kề thì cần cặp cạnh góc vuông kề với hai góc nhọn C^ và P^ của hai tam giác này bằng nhau, tức là bổ sung thêm điều kiện AC = MP.

    Câu 4: Cho tam giác PQR và tam giác TUV có P^=T^=90°; Q^=U^. Cần thêm một điều kiện gì để tam giác PQR và tam giác TUV theo trường hợp cạnh góc vuông - góc nhọn kề:

    A. PQ = TV

    B. PQ = TU

    C. PR = TU

    D. QR = UV

    Đáp án: B

    Giải thích:

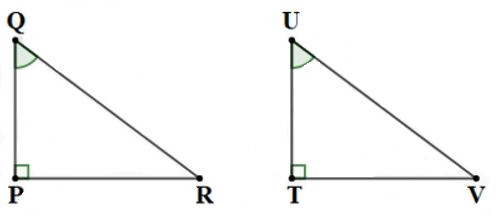
    Trắc nghiệm Trường hợp bằng nhau của hai tam giác vuông có đáp án - Toán lớp 7 (ảnh 1)

    Ta có: Q^=U^ mà góc Q và góc U là hai góc nhọn kề của hai tam giác PQR và tam giác TUV

    Do đó: để tam giác PQR và tam giác TUV theo trường hợp cạnh góc vuông - góc nhọn kề thì cần cặp cạnh góc vuông kề với hai góc nhọn Q^ và U^ của hai tam giác này bằng nhau, tức là bổ sung thêm điều kiện PQ = TU.

    Câu 5: Cho tam giác ABC và tam giác DEF có: B^=E^=90°; AC = DF; A^=F^

    Phát biểu nào trong các phát biểu sai đây là đúng

    A. △ABC=△FED

    B. △ABC=△FDE

    C. △BAC=△FED

    D. △ABC=△DEF 

    Đáp án: A

    Giải thích:

    Xét tam giác ABC và tam giác FED có:

    B^=E^=90° (gt)

    AC = DF (gt)

    A^=F^ (gt)

    ⇒△ABC=△FED (cạnh huyền - góc nhọn)

    Câu 6: Cho tam giác ABC và tam giác DEF có AB = DE; B^=E^; A^=D^=90°. Biết AC = 9cm. Độ dài DF là:

    A. 10 cm

    B. 5 cm

    C. 9 cm

    D. 7 cm

    Đáp án: C

    Giải thích:

    Xét tam giác ABC và tam giác DEF có:

    AB = DE;

    B^=E^

    A^=D^=90°

    ⇒△ABC=△DEF (cạnh góc vuông - góc nhọn)

    Suy ra DE = AC = 9cm (hai cạnh tương ứng)

    Câu 7: Cho tam giác ABC và tam giác DEF có AB=DE, B^=E^, A^=D^=90°. Biết AB=9cm, AC=12cm . Độ dài EF là:

    A. 12 cm

    B. 9 cm

    C. 15 cm

    D. 13 cm

    Đáp án: C

    Giải thích:

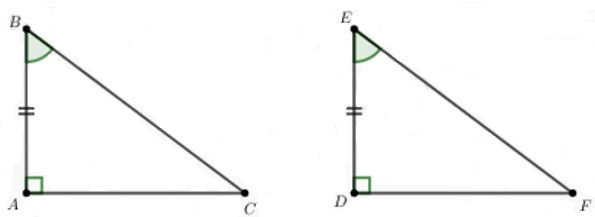
    Trắc nghiệm Trường hợp bằng nhau của hai tam giác vuông có đáp án - Toán lớp 7 (ảnh 1)

    Áp dụng định lí Pytago vào tam giác vuông ABC, ta có:

    BC2=AB2+AC2⇒BC2=92+122=225⇒BC=15cm

    Xét tam giác ABC và tam giác DEF có:

    AB=DEB^=E^A^=D^=90°

    ⇒△ABC=△DEF (cạnh góc vuông - góc nhọn kề)

    ⇒BC=EF=15cm (hai cạnh tương ứng)

    Câu 8: Cho tam giác DEF và tam giác HKI có D^=H^=90°, E^=K^, DE=HK. Biết F^=80°. Số đo góc I là:

    A. 70°

    B. 80°

    C. 90°

    D. 100°

    Đáp án: C

    Giải thích:

    Xét tam giác DEF và tam giác HKI có

    D^=H^=90°E^=K^DE=HK

    ⇒△DEF=△HKI (cạnh góc vuông - góc nhọn)

    ⇒F^=I^=80° (hai góc tương ứng)

    Câu 9: Cho hình vẽ. Chọn câu đúng

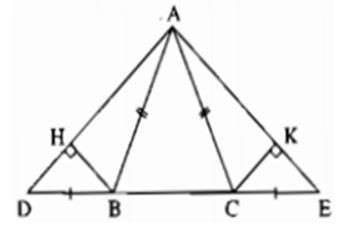
    Trắc nghiệm Trường hợp bằng nhau của hai tam giác vuông có đáp án - Toán lớp 7 (ảnh 1)

    A. △HAB=△AKC

    B. △ABH=△AKC

    C. △AHB=△ACK

    D. △AHB=△AKC

    Đáp án: D

    Giải thích:

    Vì tam giác ABC cân tại A (do AB = AC) nên ABC^=ACB^ (tính chất)(1)

    Lại có: ABC^+ABD^=180° và ACB^+ACE^=180° (hai góc kề bù)

    Suy ra:

    ABD^=180°-ABC^

    ACE^=180°-ACB^ (2)

    Từ (1) và (2) suy ra ABD^=ACE^

    Xét tam giác ABD và tam giác ACE có:

    AB = AC

    ABD^=ACE^cmt

    BD = CE

    ⇒△ABD=△ACEc-g-c

    ⇒DAB^=CAE^ (hai góc tương ứng)

    Xét tam giác AHB và AKC có:

    H^=K^=90°

    AB = AC

    DAB^=CAE^cmt

    ⇒△AHB=△AKCch-gn

    Câu 10: Cho tam giác ABC có M là trung điểm của BC và AM là tia phân giác của góc A. Khi đó, tam giác ABC là tam giác gì?

    A. △BAC cân tại B

    B. △BAC cân tại C

    C. △BAC đều

    D. △BAC cân tại A

    Đáp án: D

    Giải thích:

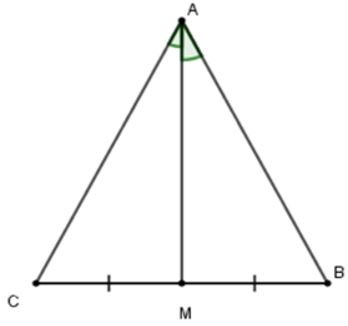
    Trắc nghiệm Trường hợp bằng nhau của hai tam giác vuông có đáp án - Toán lớp 7 (ảnh 1)

    Tam giác ABC có AM vừa là đường trung tuyến vừa là đường phân giác nên cân tại A

    Câu 11: Cho tam giác ABC cân tại A có: AH⊥BC tại H. Tính số đo góc BAH biết BAC^=50°

    A. 30°

    B. 25°

    C. 20°

    D. 35°

    Đáp án: B

    Giải thích:

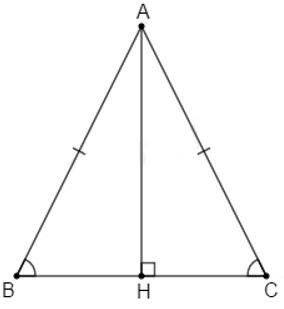
    Trắc nghiệm Trường hợp bằng nhau của hai tam giác vuông có đáp án - Toán lớp 7 (ảnh 1)

    △ABC cân tại A, suy ra AB=AC, B^=C^

    Xét hai tam giác vuông AHB và AHC có:

    AHB^=AHC^=90°AB=ACcmtB^=C^

    ⇒△AHB=△AHCch-gn

    ⇒BAH^=CAH^ (hai góc tương ứng)

    Mặt khác BAH^+CAH^=BAC^ suy ra:

    BAH^=CAH^=BAC^2=50°2=25°

    Câu 12: Cho tam giác ABC vuông cân tại A. Một đường thẳng d bất kì luôn đi qua A. Kẻ BH và CK vuông goc với đường thẳng d. Khi đó BH2+CK2 bằng:

    A. AC2+BC2

    B. BH2

    C. AC2

    D. BC2

    Đáp án: C

    Giải thích:

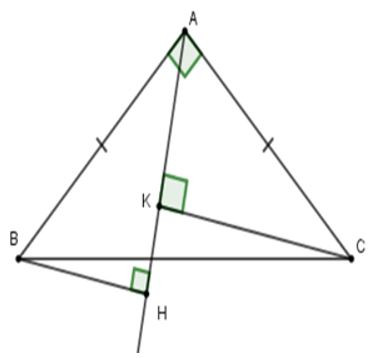
    Trắc nghiệm Trường hợp bằng nhau của hai tam giác vuông có đáp án - Toán lớp 7 (ảnh 1)

    Vì △ABC vuông cân tại A nên AB=AC (tính chất)

    Lại có: ABH^+BAH^=90° (vì △ABH vuông tại H) và CAH^+BAH^=90°

    Nên ABH^=CAK^ (cùng phụ với BAH^)

    ⇒△ABH=△CAK (cạnh huyền - góc nhọn) suy ra BH=AK

    Do đó BH2+CK2=AK2+CK2(1)

    Xét tam giác ACK, theo định lí Pytago:

    AK2+CK2=AC2 (2)

    Từ (1)và (2) suy ra BH2+CK2=AC2

    Câu 13: Cho tam giác ABC vuông cân tại A, có AC = 8cm. Một đường thẳng d bất kì luôn đi qua A. Kẻ BH và CK vuông góc với đường thẳng d. Khi đó BH2+CK2 bằng:

    A. 46

    B. 16

    C. 64

    D. 48

    Đáp án: C

    Giải thích:

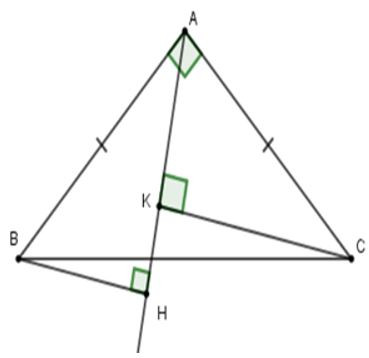
    Trắc nghiệm Trường hợp bằng nhau của hai tam giác vuông có đáp án - Toán lớp 7 (ảnh 1)

    Vì △ABC vuông cân tại A nên AB=AC (tính chất)

    Lại có: ABH^+BAH^=90° (vì △ABH vuông tại H) và CAH^+BAH^=90°

    Nên ABH^=CAK^ (cùng phụ với BAH^)

    ⇒△ABH=△CAK (cạnh huyền - góc nhọn) suy ra BH=AK

    Do đó BH2+CK2=AK2+CK2(1)

    Xét tam giác ACK, theo định lí Pytago:

    AK2+CK2=AC2 (2)

    Từ (1)và (2) suy ra 

    BH2+CK2=AK2+CK2=AC2=82=64cm

    Các câu hỏi trắc nghiệm Toán lớp 7 có đáp án, chọn lọc khác:

    Trắc nghiệm Bài ôn tập chương 2 hình học có đáp án

    Trắc nghiệm Quan hệ giữa góc và cạnh đối diện trong tam giác có đáp án

    Trắc nghiệm Quan hệ giữa đường vuông góc và đường xiên. Đường xiên và hình chiếu của đường xiên có đáp án

    Trắc nghiệm Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức trong tam giác có đáp án

    Trắc nghiệm Tính chất ba đường trung tuyến trong tam giác có đáp án

    Tham khảo các loạt bài Trắc nghiệm lớp 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,896 04/04/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: