Trắc nghiệm Tính chất đường trung trực của một đoạn thẳng có đáp án - Toán lớp 7

Đáp án: D

Giải thích:

Ba đường trung trực của một tam giác cùng đi qua 1 điểm. Điểm này cách đều ba đỉnh của tam giác và là tâm của đường tròn ngoại tiếp tam giác đó. Chọn đáp án D.

Đáp án: C

Giải thích:

Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó. Vậy C đúng.

Đáp án: B

Giải thích:

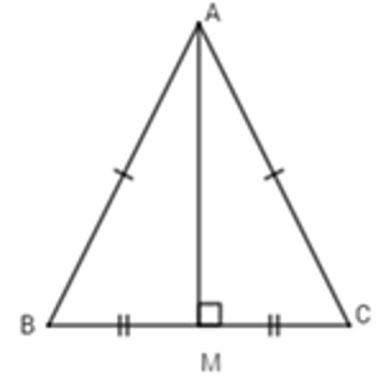
Gỉa sử ΔABC có AM là trung tuyến đồng thời là đường trung trực. Ta sẽ chứng minh ΔABC là tam giác cân. Thật vậy, vì AM là trung tuyến của ΔABC (gt)

⇒ BM = MC (tính chất trung tuyến)

Vì AM là trung trực của BC ⇒ AM ⊥ BC

Xét hai tam giác vuông ΔABM và ΔACM có:

BM = MC (cmt)

AM chung

$\Rightarrow △\mathrm{ABM}=△\mathrm{ACM}$ (2 cạnh góc vuông)

Suy ra AB = AC (2 cạnh tương ứng)

Suy ra tam giác ABC cân tại A

Đáp án: B

Giải thích:

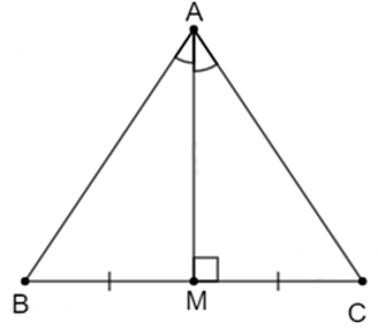
Gỉa sử ΔABC có AM là đường phân giác đồng thời là đường trung trực ứng với cạnh BC

Vì AM là đường phân giác của $\widehat{\mathrm{BAC}}\Rightarrow \widehat{\mathrm{BAM}}=\widehat{\mathrm{CAM}}$ (tính chất tia phân giác)

Vì AM là đường trung trực của BC nên

$$\begin{gathered} \mathrm{AM}\perp \mathrm{BC}\Rightarrow \widehat{\mathrm{AMB}}=\widehat{\mathrm{AMC}}=90° \\ \mathrm{Xét} △\mathrm{ABM} \mathrm{và} △\mathrm{ACM} \mathrm{có}: \\ \widehat{\mathrm{AMB}}=\widehat{\mathrm{AMC}}=90°\left(\mathrm{cmt}\right) \\ \mathrm{AM} \mathrm{chung} \\ \widehat{\mathrm{BAM}}=\widehat{\mathrm{MAC}}\left(\mathrm{cmt}\right) \\ \Rightarrow △\mathrm{ABM}=△\mathrm{ACM}(\mathrm{g}.\mathrm{c}.\mathrm{g}) \\ \Rightarrow \mathrm{AB}=\mathrm{AC}\left(\mathrm{hai} \mathrm{cạnh} \mathrm{tương} \mathrm{ứng}\right) \\ \Rightarrow △\mathrm{ABC} \mathrm{cân} \mathrm{tại} \mathrm{A} \end{gathered}$$

Đáp án: A

Giải thích:

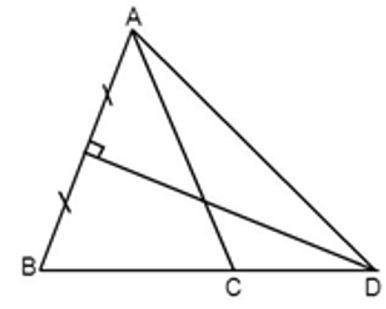
Vì ΔABC cân tại A(gt)

$\Rightarrow \hat{\mathrm{B}}=\hat{\mathrm{C}}=\left(180°-\hat{\mathrm{A}}\right):2=\left(180°-40°\right):2=70°$

Vì D thuộc đường trung trực của AB nên

⇒ AD = BD (tính chất đường trung trực của đoạn thẳng)

⇒ ΔABD cân tại D (dấu hiệu nhận biết tam giác cân)

$$\begin{gathered} \Rightarrow \widehat{\mathrm{DAC}}+\widehat{\mathrm{CAB}}=\widehat{\mathrm{DAB}}=\hat{\mathrm{B}}=70° \\ \Rightarrow \widehat{\mathrm{DAC}}=70°-\widehat{\mathrm{CAB}}=70°-40°=30° \end{gathered}$$

Đáp án: C

Giải thích:

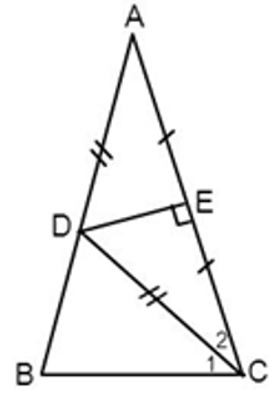
Vì đường trung trực của AC cắt AB tại D nên suy ra DA = DC (tính chất đường trung trực của đoạn thẳng)

⇒ ΔADC là tam giác cân tại D (dấu hiệu nhận biết tam giác cân)

$\Rightarrow \hat{\mathrm{A}}=\widehat{{\mathrm{C}}_2}$ (1) (tính chất tam giác cân)

Vì CD là đường phân giác của $\widehat{\mathrm{ACB}}$

$\Rightarrow \widehat{{\mathrm{C}}_1}=\widehat{{\mathrm{C}}_2}=\widehat{\mathrm{ACB}}:2$(tính chất tia phân giác)

Từ (1) và (2) $\Rightarrow \widehat{\mathrm{ACB}}=2\hat{\mathrm{A}}$

Lại có $△\mathrm{ABC}$ cân tại A (gt)

$\Rightarrow \hat{\mathrm{B}}=\widehat{\mathrm{ACB}}$ (tính chất tam giác cân)

$\Rightarrow \hat{\mathrm{B}}=2\hat{\mathrm{A}}$

Xét $△\mathrm{ABC}$ có:

$$\begin{gathered} \hat{\mathrm{B}}+\hat{\mathrm{A}}+\widehat{\mathrm{ACB}}=180° \\ \Rightarrow \hat{\mathrm{A}}+2\hat{\mathrm{A}}+2\hat{\mathrm{A}}=180° \\ \Rightarrow 5\hat{\mathrm{A}}=180°\Rightarrow \hat{\mathrm{A}}=36° \\ \Rightarrow \hat{\mathrm{B}}=\hat{\mathrm{C}}=2\hat{\mathrm{A}}=2.36°=72° \end{gathered}$$

Vậy $\hat{\mathrm{A}}=36°; \hat{\mathrm{B}}=\hat{\mathrm{C}}=72°$

Đáp án: C

Giải thích:

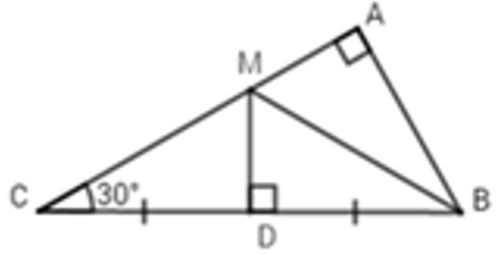
Vì M thuộc đường trung trực của BC ⇒ BM = MC

(tính chất điểm thuộc đường trung trực của đoạn thẳng)

⇒ ΔBMC cân tại M (dấu hiệu nhận biết tam giác cân)

$\Rightarrow \widehat{\mathrm{MBC}}=\hat{\mathrm{C}}=30°$ (tính chất tam giác cân)

Xét ΔABC có: $\hat{\mathrm{A}}+\widehat{\mathrm{ABC}}+\hat{\mathrm{C}}=180°$ (định lí tổng ba góc trong tam giác)

$$\begin{gathered} \Rightarrow \widehat{\mathrm{ABC}}=180°-\left(\hat{\mathrm{A}}-\hat{\mathrm{C}}\right) \\ =180°-30°-90° \\ =60° \\ \Rightarrow \widehat{\mathrm{ABM}}+\widehat{\mathrm{MBC}}=\widehat{\mathrm{ABC}}=60° \\ \Rightarrow \widehat{\mathrm{ABM}}=60°-\widehat{\mathrm{MBC}} \\ =60°-30°=30° \\ \Rightarrow \widehat{\mathrm{ABM}}=\widehat{\mathrm{MBC}} \\ \Rightarrow \mathrm{BM} \mathrm{là} \mathrm{phân} \mathrm{giác} \mathrm{của} \widehat{\mathrm{ABC}} \end{gathered}$$

Đáp án: C

Giải thích:

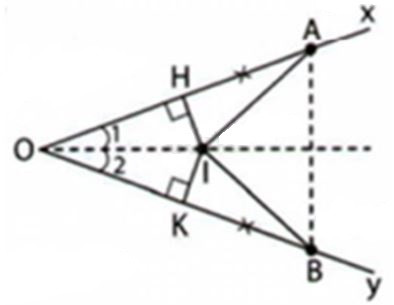
Gỉa sử đường trung trực của OA cắt OA tại H;

đường trung trực của OB cắt OB tại K

Vì HI là đường trung trực của OA nên IO = IA

(tính chất đường trung trực của đoạn thẳng)

Vì KI là đường trung trực của OB nên IO = IB

(tính chất đường trung trực của đoạn thẳng)

Do đó: IA = IB ( = IO)

Xét $△\mathrm{OIA}$ và $△\mathrm{OIB}$ có:

IA = IB (cmt)

IO chung

OA = OB (gt)

$\Rightarrow △\mathrm{OIA}=△\mathrm{OIB}(\mathrm{c}.\mathrm{c}.\mathrm{c})$

$\Rightarrow \widehat{{\mathrm{O}}_1}=\widehat{{\mathrm{O}}_2}$ (hai góc tương ứng)

Vậy OI là tia phân giác của $\widehat{\mathrm{xOy}}$

Đáp án A đúng

Theo giả thiết: OA = OB suy ra O thuộc đường trung trực của đoạn thẳng AB

Theo chứng minh trên ta có IA = IB suy ra I thuộc đường trung trực của đoạn thẳng AB

Do đó OI là đường trung trực của đoạn thẳng AB

Đáp án B đúng

Đáp án: D

Giải thích:

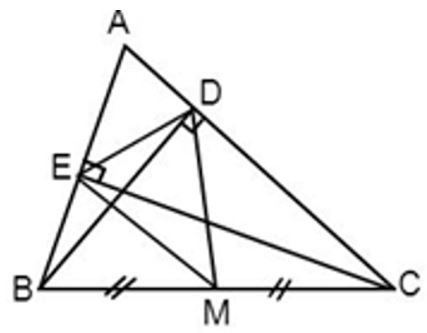
Vì M là trung điểm của BC(gt) suy ra BM = MC (tính chất trung điểm), loại đáp án A

Xét ΔBCE có M là trung điểm BC (gt) suy ra EM là trung tuyến

$\Rightarrow \mathrm{EM}=\frac{\mathrm{BC}}{2}\left(1\right)$ (trong tam giác vuông đường trung tuyến với cạnh huyền bằng nửa cạnh ấy)

Xét ΔBCD có M là trung điểm BC(gt) suy ra DM trung tuyến

$\Rightarrow \mathrm{DM}=\mathrm{MB}=\frac{\mathrm{BC}}{2}\left(2\right)$ (trong tam giác vuông đường trung tuyến với cạnh huyền bằng nửa cạnh ấy)

Từ (1) và (2) ⇒ EM = DM ⇒ M thuộc đường trung trực DE.

Loại đáp án B, chọn đáp án D

Đáp án: C

Giải thích:

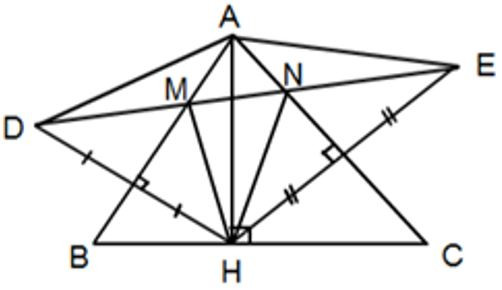
Vì AB là trung trực của HD (gt) $\Rightarrow \mathrm{AD}=\mathrm{AH}$ (tính chất trung trực của đoạn thẳng)

Vì AC là trung trực của HE (gt) $\Rightarrow \mathrm{AH}=\mathrm{AE}$ (tính chất trung trực của đoạn thẳng)

$\Rightarrow \mathrm{AD}=\mathrm{AE}\Rightarrow △\mathrm{ADE}$ cân tại A. Nên A đúng

+) M nằm trên đường trung trực của HD nên $\mathrm{MD}=\mathrm{MH}$ (tính chất trung trực của đoạn thẳng)

Xét $△\mathrm{AMD}$ và $△\mathrm{AMH}$ có:

MD = MH (cmt)

AD = AH (cmt)

AM chung

$\Rightarrow △\mathrm{AMD}=△\mathrm{AMH}\left(\mathrm{c}.\mathrm{c}.\mathrm{c}\right)$

$\Rightarrow \widehat{\mathrm{MDA}}=\widehat{\mathrm{MHA}}$ (hai góc tương ứng)

Lại có, N là đường trung trực của HE nên $\mathrm{NH}=\mathrm{NE}$ (tính chất trung trực của đoạn thẳng)

+) Xét $△\mathrm{AHN}$ và $△\mathrm{AEN}$ có:

AN cạnh chung

AH = AE (cmt)

NH = NE (cmt)

$\Rightarrow △\mathrm{AHN}=△\mathrm{AEN}\left(\mathrm{c}.\mathrm{c}.\mathrm{c}\right)$

$\Rightarrow \widehat{\mathrm{NHA}}=\widehat{\mathrm{NEA}}$ (2 cạnh tương ứng)

Mà $△\mathrm{ADE}$ cân tại A(cmt) $\Rightarrow \widehat{\mathrm{MDA}}=\widehat{\mathrm{NEA}}\Rightarrow \widehat{\mathrm{MHA}}=\widehat{\mathrm{NHA}}$.

Vậy HA là đường phân giác của $\widehat{\mathrm{MHN}}$

Đáp án: C

Giải thích:

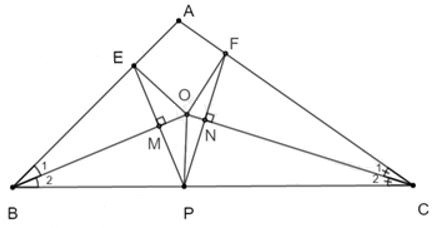
Gỉa sử $\mathrm{EP}\perp \mathrm{BO}$ tại M; $\mathrm{PF}\perp \mathrm{OC}$ tại N

Khi đó: $\widehat{\mathrm{BME}}=\widehat{\mathrm{BMP}}=90°$; $\widehat{\mathrm{CNF}}=\widehat{\mathrm{PNC}}=90°$

Vì BO là tia phân giác của $\widehat{\mathrm{ABC}}$(gt) nên $\widehat{{\mathrm{B}}_1}=\widehat{{\mathrm{B}}_2}$ (tính chất tia phân giác)

Xét $△\mathrm{BME}$ và $△\mathrm{BMP}$ có:

$\widehat{\mathrm{BME}}=\widehat{\mathrm{BMP}}=90°\left(\mathrm{cmt}\right)$

BM chung

$\widehat{{\mathrm{B}}_1}=\widehat{{\mathrm{B}}_2}$

$\Rightarrow △\mathrm{BME}=△\mathrm{BMP}\left(\mathrm{g}.\mathrm{c}.\mathrm{g}\right)$

$\Rightarrow \mathrm{ME}=\mathrm{MP}$ (hai cạnh tương ứng)

Mặt khác $\mathrm{EP}\perp \mathrm{BO}$ (gt)

Vậy OB là đường trung trực của đoạn EP (định nghĩa đường trung trực của đoạn thẳng). Đáp án A đúng

Chứng minh tương tự ta có: $△\mathrm{CNF}=△\mathrm{BMP}\left(\mathrm{g}.\mathrm{c}.\mathrm{g}\right)$ $\Rightarrow \mathrm{NF}=\mathrm{NP}$ (hai cạnh tương ứng)

Mặt khác $\mathrm{PF}\perp \mathrm{OC}\left(\mathrm{gt}\right)$

Vậy OC là đường trung trực của đoạn PF(định nghĩa đường trung trực của đoạn thẳng). Đáp án B đúng

Đáp án: C

Giải thích:

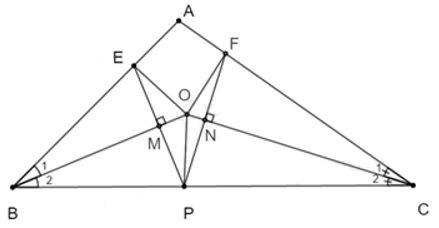
Theo câu trước ta có: $△\mathrm{BME}=△\mathrm{BMP}\left(\mathrm{g}.\mathrm{c}.\mathrm{g}\right)$ suy ra $\mathrm{BE}=\mathrm{BP}$ (hai cạnh tương ứng)

Theo câu trước ta có: $\text{△CNF=△BMP}\left(\mathrm{g}.\mathrm{c}.\mathrm{g}\right)$ suy ra $\mathrm{CF}=\mathrm{CP}$ (hai cạnh tương ứng)

Khi đó: $\mathrm{BE}+\mathrm{CF}=\mathrm{BP}+\mathrm{CP}=\mathrm{BC}$

Đáp án: D

Giải thích:

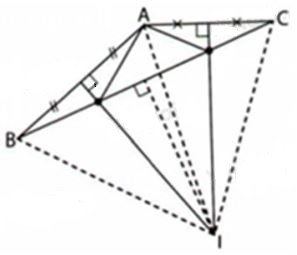
Vì $△\mathrm{ABC}$ có các đường trung trực của các cạnh AB và AC cắt nhau tại I nên $\mathrm{IA}=\mathrm{IB}=\mathrm{IC}$ (tính chất ba đường trung trực của tam giác)

Xét $△\mathrm{IAB}$ có: $\mathrm{IA}=\mathrm{IB}\left(\mathrm{cmt}\right)\Rightarrow △\mathrm{IAB}$ cân tại I (dấu hiệu nhận biết tam giác cân)

$\Rightarrow \widehat{\mathrm{IAB}}=\widehat{\mathrm{IBA}}$ (tính chất tam giác cân)

Xét $△\mathrm{IAC}$ có $\mathrm{IA}=\mathrm{IC}\left(\mathrm{cmt}\right)\Rightarrow △\mathrm{IAC}$ cân tại I (dấu hiệu nhận biết tam giác cân)

$\Rightarrow \widehat{\mathrm{IAC}}=\widehat{\mathrm{ICA}}$ (tính chất tam giác cân)

Trong $△\mathrm{IAB}$ có: $\widehat{\mathrm{BIA}}+\widehat{\mathrm{IAB}}+\widehat{\mathrm{IBA}}=180°$ (định lí tổng ba góc trong tam giác)

Mà $\widehat{\mathrm{IAB}}=\widehat{\mathrm{IBA}}$ (cmt) nên suy ra $\widehat{\mathrm{BIA}}=180°-\left(\widehat{\mathrm{IAB}}+\widehat{\mathrm{IBA}}\right)=180°-2\widehat{\mathrm{IAB}}$

Trong $△\mathrm{IAC}$ có $\widehat{\mathrm{CIA}}+\widehat{\mathrm{IAC}}+\widehat{\mathrm{ICA}}=180°$ (định lí tổng ba góc trong tam giác)

Mà $\widehat{\mathrm{IAC}}=\widehat{\mathrm{ICA}}$ (cmt) suy ra:

$\widehat{\mathrm{CIA}}=180°-\left(\widehat{\mathrm{IAC}}+\widehat{\mathrm{ICA}}\right)=180°-2\widehat{\mathrm{IAC}}$

Khi đó:

$$\begin{gathered} \widehat{\mathrm{BIC}}=\widehat{\mathrm{BIA}}+\widehat{\mathrm{AIC}} \\ =180°-2\widehat{\mathrm{IAB}}+180°-2\widehat{\mathrm{IAC}} \\ =360°-2\left(\widehat{\mathrm{IAB}}+\widehat{\mathrm{IAC}}\right) \\ =360°-2\widehat{\mathrm{BAC}} \\ =360°-2.140°=80° \end{gathered}$$