Trắc nghiệm Trường hợp bằng nhau thứ hai của hai tam giác cạnh - góc - cạnh có đáp án - Toán lớp 7
Bộ 25 bài tập trắc nghiệm Toán lớp 7 Bài 4: Trường hợp bằng nhau thứ hai của hai tam giác cạnh - góc - cạnh có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 7 Bài 4.
Trắc nghiệm Toán 7 Bài 4: Trường hợp bằng nhau thứ hai của hai tam giác
cạnh - góc - cạnh
Bài giảng Trắc nghiệm Toán 7 Bài 4: Trường hợp bằng nhau thứ hai của hai tam giác
cạnh - góc - cạnh
Câu 1: Cho đoạn thẳng BD và EC cắt nhau tại A sao cho AB = AC, AD = AE, AB > AD. Phát biểu nào trong các phát biểu sau đây sai.
A.
B.
C.
D.
Đáp án: C
Giải thích:
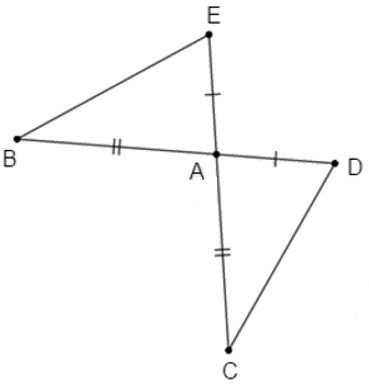
Xét và có:
AB = AC (gt)
AE = AD (gt)
(hai góc đối đỉnh)
nên A đúng
BE = CD (hai cạnh tương ứng)
nên B đúng
(hai góc tương ứng )
nên D đúng
Câu 2: Cho tam giác ABC có , M là trung điểm của AC. Trên tia đối của tia MB lấy K sao cho . Chọn câu đúng nhất
A.
B. AK//BC
C. AK = CB
D. Cả A,B,C đều đúng
Đáp án: D
Giải thích:
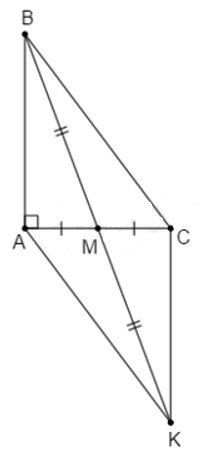
Xét và có:
AM = CM (vì M là trung điểm AC)
MB = MK (gt)
(hai góc đối đỉnh)
(hai góc tương ứng)
Mà (vì vuông tại A) suy ra
Do đó: nên A đúng
Xét và có
AM = CM (vì M là trung điểm của AC)
MK= MB (gt)
(hai góc đối đỉnh)
AK = CB (hai cạnh tương ứng)
(hai góc tương ứng)
Mà và ở vị trí so le trong nên AK//BC (B đúng)
Câu 3: Cho góc nhọn xOy và Oz là tia phân giác của góc đó. Trên tia Ox lấy điểm A và trên tia Oy lấy điểm B sao cho OA = OB. Gọi C là một điểm bất kì trên tia Oz
3.1: Chọn câu sai
A. AC = OB
B. AC = BC
C.
D. CO là tia phân giác của
Đáp án: A
Giải thích:
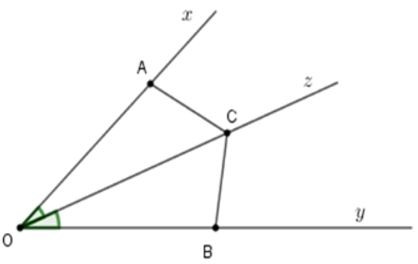
Xét tam giác AOC và BOC có:
OA = OB (gt)
(tính chất tia phân giác)
Cạnh OC chung
(hai cạnh tương ứng);
(hai góc tương ứng)
Từ đó CO là tia phân giác của
Nên B, C, D đúng, A sai
3.2: Gọi I là giao của AB và Oz. Tính góc AIC
A.
B.
C.
D.
Đáp án: B
Giải thích:
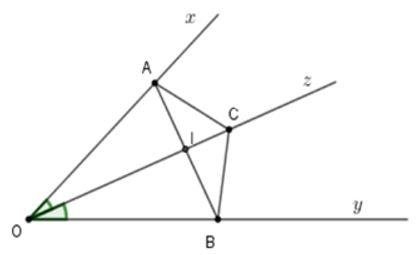
Xét tam giác AOI và BOI có:
OA = OB (gt)
(tính chất tia phân giác)
Cạnh OI chung
Do đó (hai góc tương ứng) mà nên
Hay
Câu 4: Cho tam giác MNP và tam giác IJK có MN = IJ; ; MP = IK.
Phát biểu nào trong các phát biểu sau đây đúng
A.
B.
C.
D.
Đáp án: B
Giải thích:
Xét và có:
MN = IJ
MP = IK
Câu 5: Cho đoạn thẳng BD và EC vuông góc với nhau tại A sao cho , , . ; ; .
Phát biểu nào trong các phát biểu sau đây sai.
A.
B. BC = ED
C. EB = CD
D.
Đáp án: C
Giải thích:
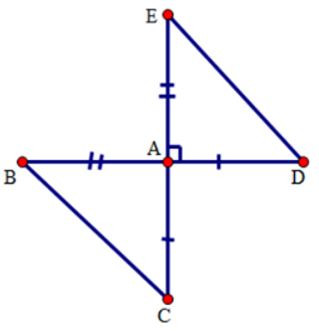
Xét hai tam giác AED và tam giác ABC có:
AB = AE
AD = AC
(2 góc đối đỉnh)
nên A đúng
Suy ra (2 cạnh tương ứng) nên B đúng
(hai góc tương ứng ) nên D đúng
Câu 6: Cho tam giác ABC có , tia phân giác BD của góc B . Trên cạnh BC lấy điểm E sao cho BE = BA. Hai góc nào sau đây bằng nhau
A.
B.
C.
D.
Đáp án: C
Giải thích:
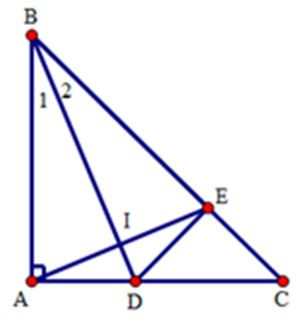
Xét tam giác BDA cà BDE có:
BA = BE (gt)
(do BD là tia phân giác của góc B)
BD là cạnh chung
(hai góc tương ứng)
Trong các tam giác ABC và EDC vuông tạo A và E, ta có:
và
suy ra
Câu 7: Cho hai đoạn thẳng AB và CD cắt nhau tại O là trung điểm của mỗi đoạn thẳng đó. Lấy E,F lần lượt là điểm thuộc đoạn AD và BC sao cho . Cho , tính EF
A. 5 cm
B. 10 cm
C. 7 cm
D. 7,5 cm
Đáp án: B
Giải thích:
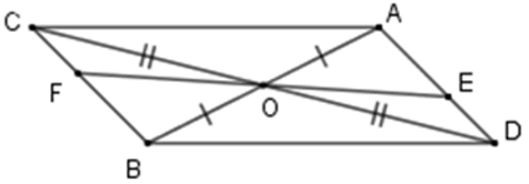
Xét tam giác OBC và OAD có:
OA = OB (gt)
OC = OD (gt)
(đối đỉnh)
(hai góc tương ứng)
Xét tam giác OBF và OAE có:
OA = OB (gt)
BF = AE (gt)
(cmt)
(hai cạnh tương ứng)
(hai góc tương ứng)
Mà (hai góc kề bù)
Suy ra ba điểm F; O; E thẳng hàng và nên O là trung điểm của EF
Câu 8: Cho tam giác ABC có , , tia phân giác BD của góc B. Trên cạnh BC lấy điểm E sao cho . Tính số đo góc EDC
A.
B.
C.
D.
Đáp án: C
Giải thích:
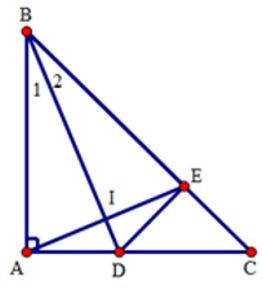
Xét tam giác BDA cà BDE có:
BA = BE (gt)
(do BD là tia phân giác của góc B)
BD là cạnh chung
(hai góc tương ứng)
BD là tia phân giác của
vuông tại A nên ta có:
Do đó
Ta có: (kề bù)
Câu 9: Cho đoạn thẳng AB, trên đường trung trực d của đoạn AB lấy điểm M. So sánh AM và BM
A. MA = MB
B. MA > MB
C. MA < MB
D. 2MA = MB
Đáp án: A
Giải thích:
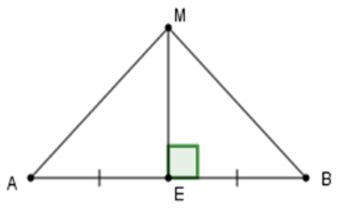
Đường trung trực của AB vuông góc với AB tại trung điểm E.
Do đó
Xét tam giác MEA và tam giác MEB có:
EA = EB (cmt)
Cạnh ME chung
MA = MB (hai cạnh tương ứng)
Câu 10: Cho tam giác ABC có M, N lần lượt là trung điểm của AB, AC. Trên tia đối của tia MC lấy D sao cho . Trên tia đối của tia NB lấy điểm E sao cho
(I)
(II)
(III) A, D, E thẳng hàng
(IV) A là trung điểm của đoạn thẳng DE
Số khẳng định đúng trong các khẳng định trên là
A. 0
B. 2
C. 4
D. 3
Đáp án: C
Giải thích:
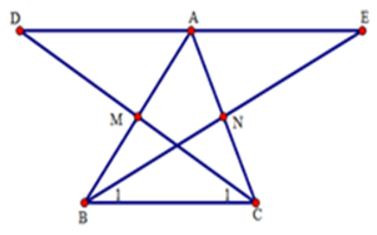
(I) Xét và có:
DM = MC (gt)
(hai góc đối đỉnh)
AM = BM (gt)
nên (I) đúng
(II) Xét và có:
AN = NC (gt)
(hai góc đối đỉnh)
NB = NE (gt)
nên (II) đúng
(III) Do nên (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên AD//BC
Do nên (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên AE//BC
Như vậy qua A có hai đường thẳng AD, AE cùng song song với BC.
Do đó D, A, E thẳng hàng (1) nên (III) đúng
(IV) Ta có AD = BC (do )
(do )
(2)
Từ (1) và (2) suy ta A là trung điểm DE
Vậy cả (I), (II), (III), (IV) đều đúng
Câu 11: Cho tam giác ABC và tam giác DEF có: , . Cần thêm một điều kiện gì để tam giác ABC và tam giác DEF bằng nhau theo trường hợp cạnh-góc-cạnh
A.
B. BC = EF
C.
D.
Đáp án: C
Giải thích:
Để tam giác ABC và tam giác DEF bằng nhau theo trường hợp cạnh – góc – cạnh cần thêm điều kiện về cạnh kề đó là:
Câu 12: Cho hai đoạn thẳng AB và CD cắt nhau tại O là trung điểm của mỗi đoạn thẳng đó. Lấy E, F lần lượt là điểm thuộc đoạn AD và BC sao cho . Cho , tính EF.
A. 4 cm
B. 2 cm
C. 3 cm
D. 3,5 cm
Đáp án: A
Giải thích:
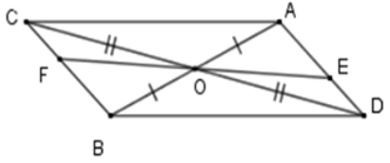
Xét tam giác OBC và OAD có:
OA = OB (gt)
OC = OD (gt)
(đối đỉnh)
(hai góc tương ứng)
Xét tam giác OBF và OAE có:
OA = OB (gt)
BF = AE (gt)
(cmt)
(hai cạnh tương ứng)
(hai góc tương ứng)
Mà (hai góc kề bù)
Suy ra ba điểm F; O; E thẳng hàng và nên O là trung điểm của EF
Câu 13: Cho tam giác ABC và tam giác MHK có: , . Cần thêm một điều kiện gì để tam giác ABC và tam giác MHK bằng nhau theo trường hợp cạnh-góc-cạnh
A. BC = MK
B. BC = HK
C. AC = MK
D. AC = HK
Đáp án: C
Giải thích:
Để tam giác ABC và tam giác MHK bằng nhau theo trường hợp cạnh – góc – cạnh cần thêm điều kiện về cạnh kề đó là: AC = MK
Câu 14: Cho tam giác ABC vuông tại A. Tia phân giác của góc ABC cắt AC tại D, lấy E trên BC sao cho BE = AB
14.1: Chọn câu đúng
A.
B.
C. DC = DE
D.
Đáp án: A
Giải thích:
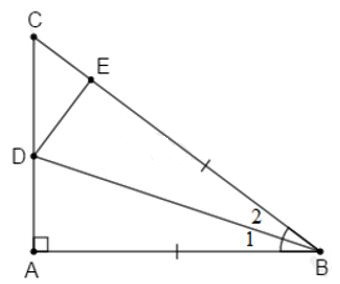
Xét và có:
BA = BE (gt)
(vì BD là tia phân giác )
BD cạnh chung
14.2: Trên tia đối của tia DE lấy điểm M sao cho . So sánh EC và AM
A. EC < AM
B. EC = AM
C. EC > AM
D. Chưa đủ điều kiện để so sánh
Đáp án: B
Giải thích:
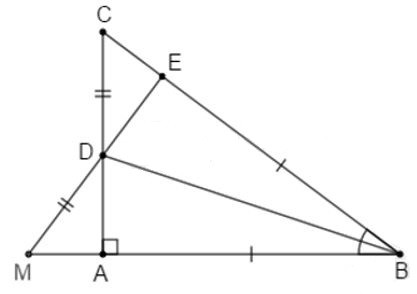
Sử dụng kết quả câu trước suy ra (hai cạnh tương ứng). Nối AM
Xét và có:
DA = DE (cmt)
DM = DC (gt)
(hai góc đối đỉnh)
(hai cạnh tương ứng bằng nhau)
14.3: Trên tia đối của tia DE lấy điểm M sao cho . Nôi AE, so sánh số đo
A.
B.
C.
D. Chưa đủ điều kiện để so sánh
Đáp án: C
Giải thích:
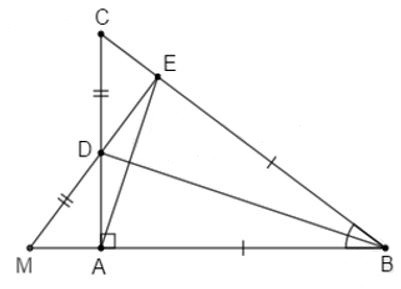
Sử dụng kết quả câu trước
; (Các cạnh tương ứng)
Ta có:
AD = ED (1)
DC = DM (2)
Cộng (1) và (2) theo vế với vế ta được
hay
Xét và có:
EC = AM (cmt)
AE chung
AC = EM (cmt)
(hai góc tương ứng)
Câu 15: Cho tam giác ABC có , tia phân giác của góc A cắt BC ở D. Trêm cạnh AC lấy E sao cho . Chọn câu đúng
A.
B.
C. AD là đường trung tuyến của BE
D.
Đáp án: C
Giải thích:
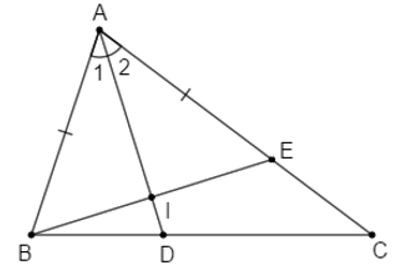
Gọi I là giao điểm của AD và BE
Xét và có:
AI cạnh chung
( Vì AD là phân giác )
AB = AE (gt)
(hai góc tương ứng)
(hai cạnh tương ứng) (1)
Mặt khác (hai góc kề bù)
Do đó (2)
Từ (1) và (2) suy ra AD là đường trung tuyến của BE
Câu 16: Cho tam giác ABC có , phân giác BD và CE cắt nhau tại O
16.1: Chọn câu đúng
A.
B.
C.
D. Cả A, B đều đúng
Đáp án: D
Giải thích:
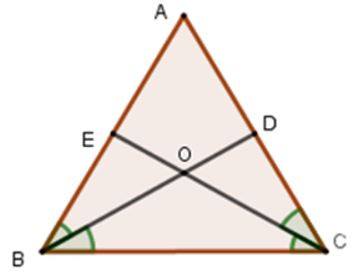
Vì BD và CE là tia phân giác của góc và
;
Xét tam giác ABD và tam giác CBD có:
(cmt)
AB = AC (gt)
BD chung
(hai góc tương ứng);
DC = AD(hai cạnh tương ứng) nên C sai
Mà (hai góc kề bù)
Nên .
Do đó
Tương ứng
16.2: Tính
A.
B.
C.
D.
Đáp án: C
Giải thích:
Từ câu trước ta có:
(hai góc tương ứng) (1)
Tương tự ta có:
(hai góc tương ứng) (2)
Từ (1) và (2) ta có: .
Mà (định lý tổng ba góc trong tam giác )
Lại có (cmt)
Xét tam giác BOC có ( định lý tổng ba góc trong tam giác )
Nên:
Vậy
Câu 17: Cho hai đường thẳng xx', yy' cắt nhau tại O. Trên xx' lấy hai điểm A,B sao cho O là trung điểm AB. Trên yy' lấy C,D sao cho O là trung điểm CD
17.1: Chọn câu đúng
A.
B.
C.
D.
Đáp án: D
Giải thích:
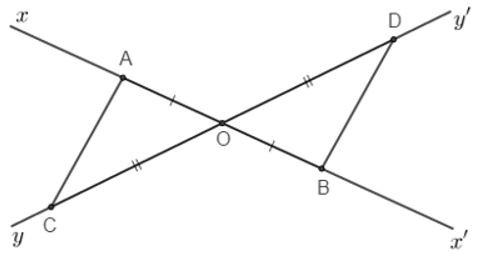
Xét và có:
OA = OB (vì O là trung điểm AB)
OC = OD (vì O là trung điểm CD)
(hai góc đối đỉnh)
17.2: So sánh AC và BD
A.
B.
C.
D.
Đáp án: A
Giải thích:
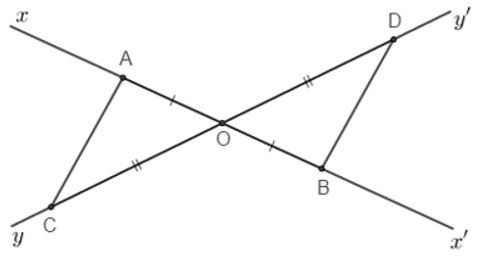
Xét và có:
OA = OB (vì O là trung điểm AB)
OC = OD (vì O là trung điểm CD)
(hai góc đối đỉnh)
(hai cạnh tương ứng)
Câu 18: Cho tam goác DEF và tam giác HKG có , , biết . Số đo góc H là:
A.
B.
C.
D.
Đáp án: A
Giải thích:
Xét tam giác DEF và tam giác HKF có
DE = HK
EF = KG
(hai góc tương ứng)
Câu 19: Cho tam goác DEF và tam giác MNP có , , , biết . Số đo góc M là:
A.
B.
C.
D.
Đáp án: D
Giải thích:
Xét và có:
DE= MN
EF = NP
(hai góc tương ứng)
Câu 20: Cho tam giác BAC và tam giác KEF có , , .
Phát biểu nào trong các phát biểu sau đây đúng
A.
B.
C.
D.
Đáp án: A
Giải thích:
Xét tam giác BAC và tam giác KEF có:
BA = EK (gt)
(gt)
CA = KF (gt)
Các câu hỏi trắc nghiệm Toán lớp 7 có đáp án, chọn lọc khác:
Trắc nghiệm Trường hợp bằng nhau thứ ba của hai tam giác góc - cạnh - góc có đáp án
Trắc nghiệm Tam giác cân có đáp án
Trắc nghiệm Định lý Py - ta - go có đáp án
Trắc nghiệm Trường hợp bằng nhau của hai tam giác vuông có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học 8 có đáp án
- Trắc nghiệm Toán lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn 8 có đáp án
- Trắc nghiệm Hóa học lớp 8 có đáp án
- Trắc nghiệm Địa Lí lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 8 có đáp án
- Trắc nghiệm GDCD lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Vật Lí lớp 8 có đáp án
- Trắc nghiệm Công nghệ lớp 8 có đáp án
- Trắc nghiệm Tin học lớp 8 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Sinh học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Toán lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Hóa học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn lớp 11 có đáp án
- Trắc nghiệm Tiếng Anh lớp 11 có đáp án
- Trắc nghiệm Vật Lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Địa lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm GDCD lớp 11 có đáp án
- Trắc nghiệm Lịch sử lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Công nghệ lớp 11 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 11 có đáp án
- Trắc nghiệm Tin học lớp 11 có đáp án
- Trắc nghiệm Toán lớp 12 có đáp án
- Trắc nghiệm Sinh học lớp 12 có đáp án
- Trắc nghiệm Hóa học lớp 12 có đáp án
- Trắc nghiệm Ngữ văn lớp 12 có đáp án
- Trắc nghiệm Tiếng Anh lớp 12 có đáp án
- Trắc nghiệm Địa lí lớp 12 có đáp án
- Trắc nghiệm Vật Lí lớp 12 có đáp án
- Trắc nghiệm Công nghệ lớp 12 có đáp án
- Trắc nghiệm Giáo dục công dân lớp 12 có đáp án
- Trắc nghiệm Lịch sử lớp 12 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 12 có đáp án
