Trắc nghiệm Trường hợp bằng nhau thứ nhất của hai tam giác canh - cạnh - cạnh có đáp án - Toán lớp 7
Bộ 23 bài tập trắc nghiệm Toán lớp 7 Bài 3: Trường hợp bằng nhau thứ nhất của hai tam giác canh - cạnh - cạnh có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 7 Bài 3.
Trắc nghiệm Toán 7 Bài 3: Trường hợp bằng nhau thứ nhất của hai tam giác
cạnh - cạnh - cạnh
Bài giảng Trắc nghiệm Toán 7 Bài 3: Trường hợp bằng nhau thứ nhất của hai tam giác
cạnh - cạnh - cạnh
Câu 1: Chọn hình dưới đây:
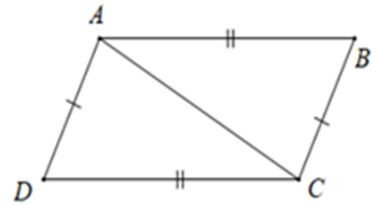
Chọn câu sai
A. AD//BC
B. AB//CD
C. △ABC=△CDA
D. △ABC=△ACD
Đáp án: D
Giải thích:
Xét tam giác ADC và CBA có:
AB = CD
AD = BC
DB chung
⇒△ADC=△CBA(c.c.c)
Do đó ^DAC=^BCA (hai góc tương ứng) mà hai góc ở vị trí so le trong nên AD//BC
Tương tự AB//DC
Vậy A, B, C đúng, D sai
Câu 2: Cho đoạn thẳng BC = 10cm. Trên một nửa mặt phẳng bờ BC vẽ tam giác ABC sao cho AC = 6cm, BC = 8cm, trên nửa mặt phẳng bờ còn lại vẽ tam giác DBC sao cho BD = 6cm, CD = 8cm. Chọn câu đúng
A. △ABC=△DBC
B. △ABC=△BCD
C. △ABC=△DCB
D. △BCA=△BCD
Đáp án: C
Giải thích:
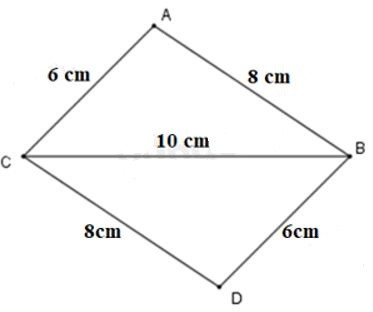
Từ bài ra ta có: AC = BD = 6cm
AB = DC = 8cm
Xét △ABC và △DCB có:
AC = DB (cmt)
AB = DC (cmt)
Cạnh BC chung
Nên △ABC=△DCB
Câu 3: Cho hai tam giác ABD và CDB có cạnh chung BD. Biết và . Phát biểu nào sau đây là sai:
A.
B.
C.
D.
Đáp án: C
Giải thích:
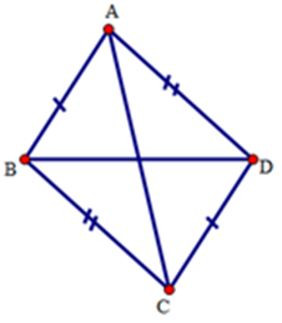
Xét và có
AB = CD (gt)
AD = BC (gt)
BD chung
(góc tương ứng)
Vậy đáp án C là sai
Câu 4: Cho , vẽ cung tròn tâm O bán kính 2 cm, cung tròn này cắt Ox và Oy lần lượt ở A và B. Vẽ các cung tròn bán kính tâm A và B có bán kính 3 cm, chúng cắt nhau tại điểm C nằm trong góc xOy. Tính
A.
B.
C.
D.
Đáp án: A
Giải thích:
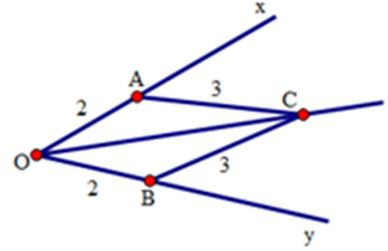
Xét hai tam giác OAC và OBC có:
OA = OB = 2cm
OC chung
AC = BC = 3cm
(hai góc tương ứng)
Mà
Vậy
Câu 5: Cho tam giác MNP có MN = MP. Gọi A là trung điểm của NP. Biết thì số đo góc MPN là
A.
B.
C.
D.
Đáp án: B
Giải thích:
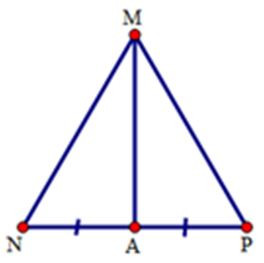
Xét tam giác NAM và tam giác PAM có:
MN = MP
NA = PA
MA chung
Suy ra: (hai góc tương ứng)
Ta có: (cmt). Xét tam giác MNP có:
Câu 6: Cho tam giác ABC và tam giác DEF có:
AB = DE; BC = EF; AC = DF
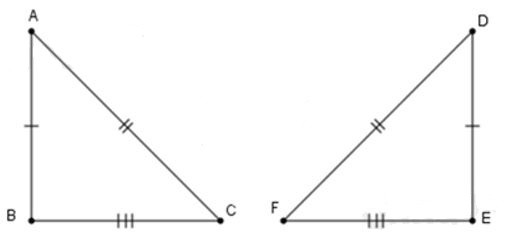
6.1: Phát biểu nào trong các phát biểu sau đây là đúng:
A.
B.
C.
D.
Đáp án: B
Giải thích:
Xét và có:
AB = DE (gt)
BC = EF (gt)
AC = DF (gt)
6.2:
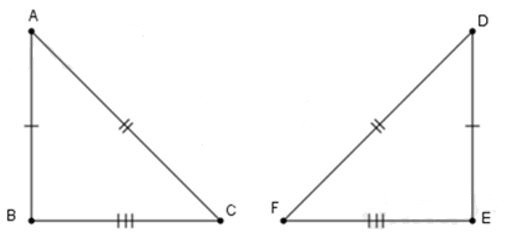
Nếu , thì số đo là
A.
B.
C.
D.
Đáp án: A
Giải thích:
Xét và có:
AB = DE (gt)
BC = EF (gt)
AC = DF (gt)
(hai góc tương ứng bằng nhau)
Câu 7: Cho tam giác ABC có AB < AC. Gọi sao cho AB = CE. Gọi O là một điểm nằm ở trong tam giác sao cho OA = OC, OB = OE. Khi đó:
A.
B.
C.
D.
Đáp án: B
Giải thích:
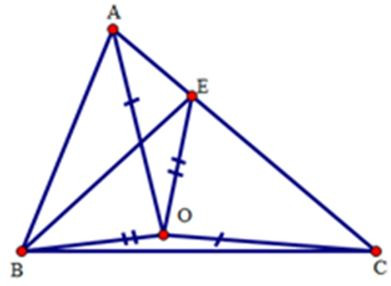
Xét tam giác AOB và tam giác COE có:
AO = CO (gt)
OB = OE (gt)
AB = CE (gt)
Suy ra ; (hai góc tương ứng)
Nên A, C, D sai, B đúng
Câu 8: Cho đoạn thẳng AB, điểm C cách đều hai điểm A và B, điểm D cách đều hai điểm A và B
8.1: Hai điểm C và D nằm hai phía đối với AB. Chọn khẳng định đúng
A.
B.
C. CD là tia phân giác của góc ACB
D. AB là tia phân giác của góc CAD
Đáp án: C
Giải thích:
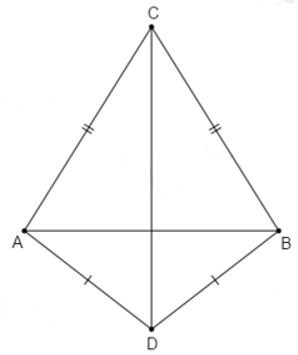
Xét và có:
AC = BC (gt)
AD = BD (gt)
CD chung
(hai góc tương ứng)
Do đó CD là tia phân giác của
8.2: Nếu C và D nằm cùng phía với AB (). Chọn câu đúng
A.
B. CD là tia phân giác của góc ACB
C. AB là tia phân giác của góc CAD
D.
Đáp án: B
Giải thích:
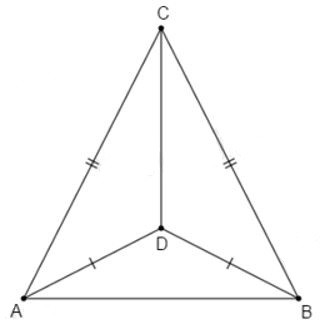
Xét và có:
AC = BC (gt)
AD = BD (gt)
CD chung
(hai góc tương ứng)
Do đó CD là tia phân giác của
Câu 9: Cho hình vẽ. Phát biểu nào sau đây là sai:
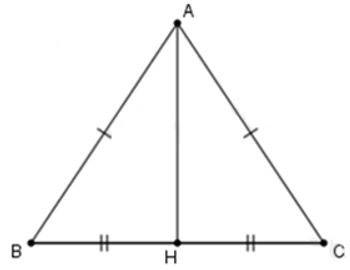
A.
B.
C.
D.
Đáp án: D
Giải thích:
Xét và có:
AB = AC (gt)
BH = CH (gt)
AH cạnh chung
(góc tương ứng)
Vậy đáp án D là sai
Câu 10: Cho hình vẽ sau. Tam giác nào bằng với tam giác ABC
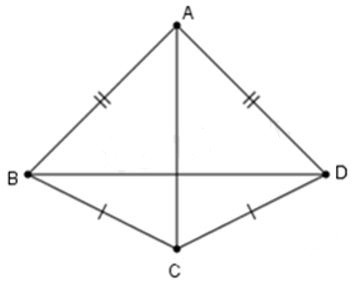
A.
B.
C.
D.
Đáp án: C
Giải thích:
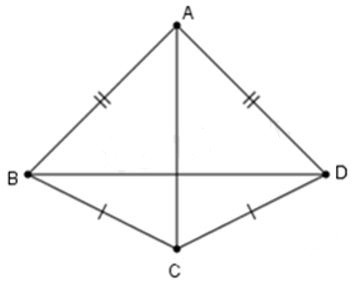
Xét có:
AC = AD (gt)
BC = DC (gt)
AC cạnh chung
Câu 11: Cho hình dưới đây:
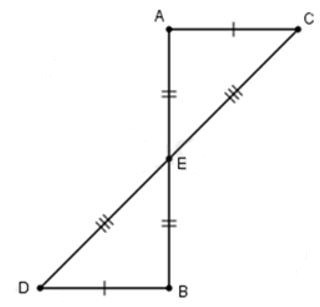
Chọn câu đúng nhất
A. AC//BD
B.
C.
D.
Đáp án: A
Giải thích:
Xét tam giác AEC và BEC có
AE = BE (gt)
CE = DE (gt)
AC = BD (gt)
(các góc tương ứng)
Mặt khác hai góc và ở vị trí so le trong nên AC//BD
Câu 12: Cho hình vẽ sau. Tam giác nào bằng với tam giác ABC
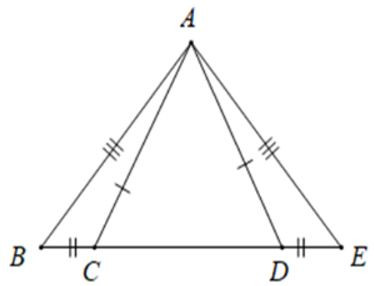
A.
B.
C.
D.
Đáp án: C
Giải thích:
Từ hình vẽ ta thấy:
AB = AE; BC = DE; AC = AD
(c - c - c)
Câu 13: Cho đoạn thẳng AC = 6cm. Trên một nửa mặt phẳng bờ AB vẽ tam giác ABC sao cho AC = 4cm, BC = 5cm, trên nửa mặt phẳng bờ còn lại vẽ tam giác ABD sao cho BD = 4cm, AD = 5cm. Chọn câu đúng
A.
B.
C.
D.
Đáp án: C
Giải thích:
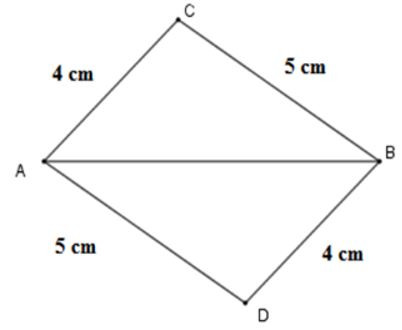
Từ bài ra ta có:
AD = BD = 4cm; BC = AD = 5cm
Xét và có:
AC = BD (cmt)
BC = AD (cmt)
Cạnh AB chung
Nên
Câu 14: Cho tam giác ABC có AB = AC và MB = MC . Chọn đáp án sai:
A.
B.
C.
D.
Đáp án: A
Giải thích:
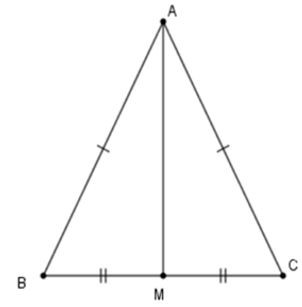
Xét và có:
AB = AC (gt)
MB = MC (gt)
Cạnh AM chung
Nên
Suy ra và (hai góc tương ứng bằng nhau) mà (hai góc kề bù)
Nên
Hay
Vậy B,C,D đúng, A sai
Câu 15: Cho tam giác MNP có MN = MP. Gọi K là trung điểm của NP. Biết thì số đo góc MPN là
A.
B.
C.
D.
Đáp án: B
Giải thích:
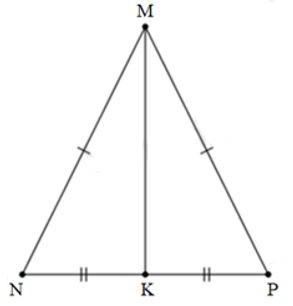
Xét và có:
MN = MP (gt)
KN = KP (vì K là trung điểm của NP)
AK chung
(hai góc tương ứng)
Ta có: (cmt), xét có:
Câu 16: Cho tam giác ABC (AB < AC). Trên tia AB lấy điểm D sao cho . E là trung điểm của DC. Từ B kẻ BK vuông góc với CD. Chọn câu đúng
A.
B.
C. AE//BK
D.
Đáp án: C
Giải thích:
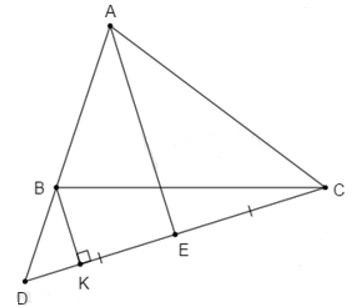
Xét và có:
AD = AC (gt)
DE = CE (vì E là trung điểm DC)
AE chung
(hai góc tương ứng)
Mặt khác (hai góc kề bù)
Hay
Theo đề bài:
Từ (1) và (2) suy ra AE//BK
Câu 17: Cho , vẽ cung tròn tâm O bán kính 3 cm, cung tròn này cắt Ox và Oy lần lượt ở A và B. Vẽ các cung tròn bán kính tâm A và B có bán kính 4 cm, chúng cắt nhau tại điểm C nằm trong góc xOy. Tính
A.
B.
C.
D.
Đáp án: B
Giải thích:
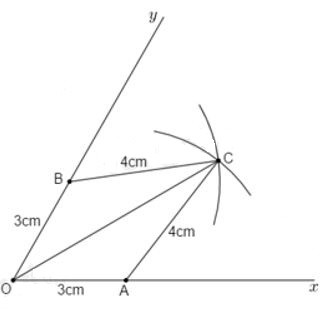
Xét hai tam giác OAC và OBC có:
OA = OB = 3cm
OC chung
AC = BC =4cm
(hai góc tương ứng)
Mà
Vậy
Câu 18: Cho có AM = AN và I là trung điểm MN. Chọn câu đúng nhất
A.
B.
C.
D. Cả A,B,C đúng
Đáp án: D
Giải thích:
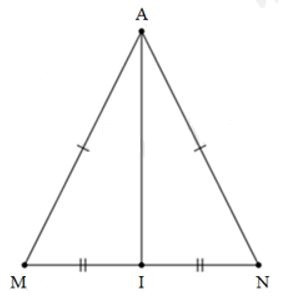
Xét và có:
AM = AN (gt)
IM = IN (I là trung điểm của MN)
AI cạnh chung
( hai góc tương ứng bằng nhau)
Mặt khác, (hai góc kề bù)
hay
Vậy A, B, C đúng
Câu 19: Trên đường thăng xy lấy hai điểm A,B. Trên cùng nửa mặt phẳng bờ xy lấy hai điểm C và C' sao cho AC = BC'; BC = AC'
19.1: Chọn câu đúng
A.
B.
C.
D.
Đáp án: D
Giải thích:
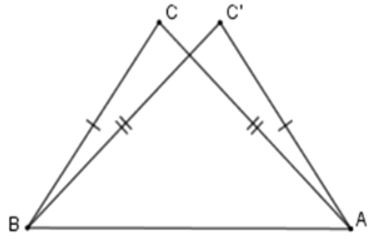
Xét hai tam giác ACB và BC'A có:
AC = BC' (gt)
BC = AC' (gt)
AB chung
Suy ra (hai góc tương ứng bằng nhau)
Nên A, B, C sai, D đúng
19.2: So sánh hai góc
A.
B.
C.
D.
Đáp án: C
Giải thích:
Vì (ý trước) ta suy ra và (1) (hai góc tương ứng)
Lại có: và (tia nằm giữa hai tia)
Suy ra và (2)
Từ (1) và (2) suy ra
Các câu hỏi trắc nghiệm Toán lớp 7 có đáp án, chọn lọc khác:
Trắc nghiệm Trường hợp bằng nhau thứ hai của hai tam giác cạnh - góc - cạnh có đáp án
Trắc nghiệm Trường hợp bằng nhau thứ ba của hai tam giác góc - cạnh - góc có đáp án
Trắc nghiệm Tam giác cân có đáp án
Trắc nghiệm Định lý Py - ta - go có đáp án
Trắc nghiệm Trường hợp bằng nhau của hai tam giác vuông có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học 8 có đáp án
- Trắc nghiệm Toán lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn 8 có đáp án
- Trắc nghiệm Hóa học lớp 8 có đáp án
- Trắc nghiệm Địa Lí lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 8 có đáp án
- Trắc nghiệm GDCD lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Vật Lí lớp 8 có đáp án
- Trắc nghiệm Công nghệ lớp 8 có đáp án
- Trắc nghiệm Tin học lớp 8 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Sinh học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Toán lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Hóa học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn lớp 11 có đáp án
- Trắc nghiệm Tiếng Anh lớp 11 có đáp án
- Trắc nghiệm Vật Lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Địa lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm GDCD lớp 11 có đáp án
- Trắc nghiệm Lịch sử lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Công nghệ lớp 11 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 11 có đáp án
- Trắc nghiệm Tin học lớp 11 có đáp án
- Trắc nghiệm Toán lớp 12 có đáp án
- Trắc nghiệm Sinh học lớp 12 có đáp án
- Trắc nghiệm Hóa học lớp 12 có đáp án
- Trắc nghiệm Ngữ văn lớp 12 có đáp án
- Trắc nghiệm Tiếng Anh lớp 12 có đáp án
- Trắc nghiệm Địa lí lớp 12 có đáp án
- Trắc nghiệm Vật Lí lớp 12 có đáp án
- Trắc nghiệm Công nghệ lớp 12 có đáp án
- Trắc nghiệm Giáo dục công dân lớp 12 có đáp án
- Trắc nghiệm Lịch sử lớp 12 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 12 có đáp án
