Trắc nghiệm Tính chất ba đường cao của tam giác có đáp án - Toán lớp 7
Bộ 20 bài tập trắc nghiệm Toán lớp 7 Bài 9: Tính chất ba đường cao của tam giác có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 7 Bài 9.
Trắc nghiệm Toán 7 Bài 9: Tính chất ba đường cao của tam giác
Câu 1: Cho tam giác nhọn ABC có hai đường cao AH và BK cắt nhau tại D
1.1: Biết , tính
A.
B.
C.
D.
Đáp án: C
Giải thích:
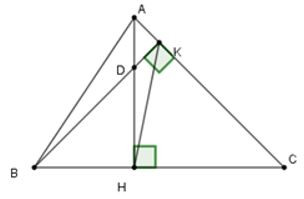
Xét tam giác CHK có (1)
(định lí tổng ba góc trong tam giác)
Xét tam giác DHK có (2)
(định lí tổng ba góc trong tam giác)
Từ (1) và (2) suy ra:
Mà ;
Suy ra:
1.2: Nếu và thì tam giác ABC là tam giác
A. Cân tại A
B. Cân tại B
C. Cân tại C
D. Đều
Đáp án: D
Giải thích:
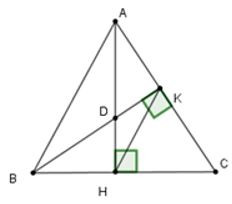
Nếu thì tam giác DAB cân tại D suy ra (1) (tính chất tam giác cân)
Xét tam giác AHB có (2)
Xét tam giác ABK có: (3)
Từ (1)(2)(3) ta suy ra hay suy ra tam giác ABC cân tại C
Lại có (gt) nên là tam giác đều
Câu 2: Trực tâm là giao của:
A. ba đường trung tuyến.
B. ba đường phân giác.
C. ba đường cao.
D. ba đường trung trực.
Đáp án: C
Giải thích:
Trực tâm của tam giác là giao của ba đường cao.
Câu 3: Cho , hai đường cao AM và BN cắt nhau tại H. Em chọn phát biểu đúng:
A. H là trọng tâm của
B. H là tâm đường tròn nội tiếp
C. CH là đường cao của
D. CH là đường trung trực của
Đáp án: C
Giải thích:
Vì hai đường cao AM và BN cắt nhau tại H nên CH là đường cao của và H là trực tâm của tam giác ABC nên A, B, D sai, C đúng
Câu 4: Cho tam giác ABC có AM là đường phân giác đồng thời cũng là đường cao, khi đó tam giác ABC là tam giác gì?
A. Tam giác vuông
B. Tam giác cân
C. Tam giác đều
D. Tam giác vuông cân
Đáp án: B
Giải thích:
Vì tam giác ABC cân tại A có AM là đường phân giác đồng thời cũng là đường cao nên là tam giác cân
Câu 5: Cho cân tại A, trung tuyến AM. Biết ; . Tính độ dài các cạnh AB và AC
A. AB = AC = 13cm
B. AB = AC = 14cm
C. AB = AC = 15cm
D. AB = AC = 16cm
Đáp án: A
Giải thích:
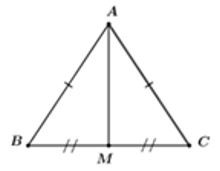
Vì cân tại A(gt) mà AM là trung tuyến nên AM cũng là đường cao của tam giác đó
Vì AM là trung tuyến của nên M là trung điểm của BC
Xét vuông tại M có: (Định lí Pytago)
Vậy AB = AC = 13cm
Câu 6: Cho cân tại A, trung tuyến AM. Biết ; . Tính độ dài các cạnh AB và AC
A. AB = AC = 5cm
B. AB = AC = 7cm
C. AB = AC = 6cm
D. AB = AC = 4cm
Đáp án: A
Giải thích:
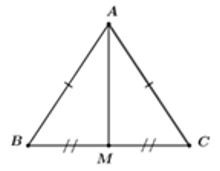
Vì cân tại A(gt) mà AM là trung tuyến nên AM cũng là đường cao của tam giác đó
Vì AM là trung tuyến của nên M là trung điểm của BC
Xét vuông tại M có: (Định lí Pytago)
Vậy AB = AC = 5cm
Câu 7: Cho tam giác ABC cân tại A có AM là đường trung tuyến khi đó:
A.
B. AM là đường trung trực của BC
C. AM là đường phân giác của góc BAC
D. Cả A, B, C đều đúng
Đáp án: D
Giải thích:
Vì tam giác ABC cân tại A có AM là đường trung tuyến nên AM cũng là đường cao, đường trung trực và đường phân giác của tam giác ABC.
Câu 8: Cho nhọn, hai đường cao BD và CE. Trên tia đối của tia BD lấy điểm I sao cho . Trên tia đối của tia CE lấy điểm K sao cho
8.1: Chọn câu đúng
A. AI > AK
B. AI < AK
C. AI = 2AK
D. AI = AK
Đáp án: D
Giải thích:
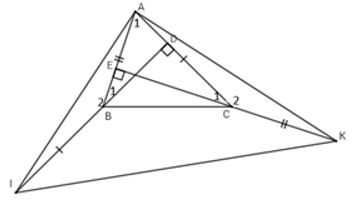
Xét có: (trong tam giác vuông 2 góc nhọn phụ nhau)
Xét có: (trong tam giác vuông2 góc nhọn phụ nhau)
(1)
Lại có: (2) (hai góc kề bù)
Từ (1) và (2)
Xét và có:
AB = CK (gt)
(cmt)
BI = AC (gt)
8.2: là tam giác gì?
A. là tam giác cân tại B
B. là tam giác vuông cân tại A
C. là tam giác vuông
D. là tam giác đều
Đáp án: B
Giải thích:
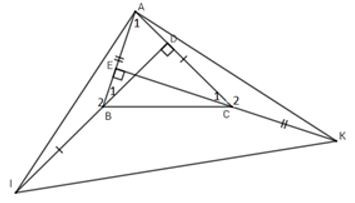
Ta có: (cmt) cân tại A (*)
(cmt)
(3) (hai góc tương ứng)
Xét có: (4) (trong tam giác vuông2 góc nhọn phụ nhau)
Từ (3),(4)
vuông tại A (**)
Từ (*)(**) vuông cân tại A
Câu 9: Cho vuông cân tại B. Trên cạnh AB lấy điểm H. Trên tia đối của tia BC lấyđiểm D sao cho
9.1: Chọn câu đúng
A.
B.
C.
D. đều
Đáp án: A
Giải thích:
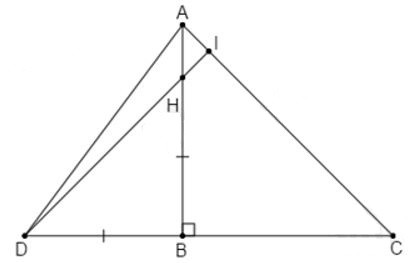
Gọi I là giao điểm của DH và AC
vuông cân tại B(gt) nên
có: ; nên vuông cân tại B suy ra hay
Xét có: suy ra
Vậy
9.2: Gọi CH cắt AD tại K. Tính số đo góc CKA
A.
B.
C.
D.
Đáp án: D
Giải thích:
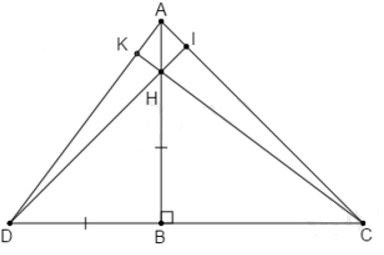
Gọi I là giao điểm của DH và AC
Sử dụng kết quả câu trước ta có:
Xét có: ; nên H là trực tâm của
Suy ra CK là đường cao thứ ba của hay
Do đó
Câu 10: Đường cao của tam giác đều cạnh a có bình phương độ dài là
A.
B.
C.
D.
Đáp án: A
Giải thích:
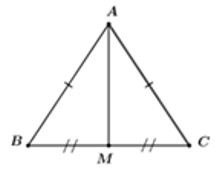
Xét tam giác ABC đều cạnh có AM là đường trung tuyến suy ra AM cũng là đường cao của tam giác ABC hay tại M
Ta có:
Xét tam giác AMC vuông tại M, theo định lí Pytago ta có:
Vậy bình phương độ dài đường cao của tam giác đều cạnh a là
Câu 11: Đường cao của tam giác đều cạnh 4 có bình phương độ dài đường cao là
A. 16
B. 12
C. 14
D. 10
Đáp án: B
Giải thích:
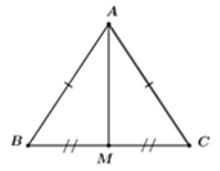
Xét tam giác ABC đều cạnh có AM là đường trung tuyến suy ra AM cũng là đường cao của tam giác ABC hay tại M
Ta có:
Xét tam giác AMC vuông tại M, theo định lí Pytago ta có:
Vậy bình phương độ dài đường cao của tam giác đều cạnh a là 12
Câu 12: Cho đoạn thẳng AB và điểm M nằm giữa A và B . Vẽ tia Mx vuông góc với AB, trên đó lấy hai điểm C và D sao cho , . Tia AC cắt BD ở E. Tính
A.
B.
C.
D.
Đáp án: D
Giải thích:
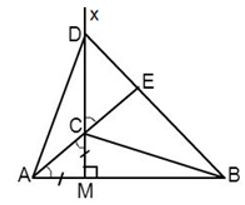
Vì
Xét có:
(tính chất tam giác cân)
Do đó (đối đỉnh)
Xét có:
(tính chất tam giác cân)
Xét có:
Lại có: (kề bù)
Câu 13: Cho có vuông tại A, đường cao AH, phân giác AD. Gọi I, J lần lượt là giao điểm các phân giác của , , E là giao điểm của đường thẳng BI và AJ. Chọn câu đúng
A. là tam giác vuông tại E
B. là tam giác vuông tại A
C. là tam giác vuông tại B
D. là tam giác đều
Đáp án: A
Giải thích:
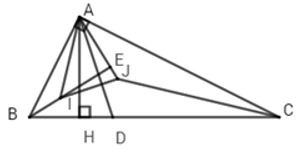
+) Ta có:
(1)
Mặt khác, BI là tia phân giác của và E thuộc BI suy ra
(2) (tính chất tia phân giác)
+) AJ là tia phân giác của (gt)
(3) (tính chất tia phân giác)
Từ (1)(2)(3)
Xét có:
vuông tại E
Câu 14: Cho tam giác ABC vuông cân tại A. Trên cạnh AB lấy điểm D, trên tia đối của tia AC lấy điểm E sao cho . Kéo dài CD cắt BE tại I. Tính số đo góc
A.
B.
C.
D.
Đáp án: D
Giải thích:
Gọi K là giao của ED và BC
vuông cân tại A(gt) nên
có: ; (gt) nên vuông cân tại A suy ra hay
Xét có: (cmt) suy ra:
Vậy
Xét có: ; nên D là trực tâm của
Suy ra CI là đường cao thứ ba của hay
Do đó
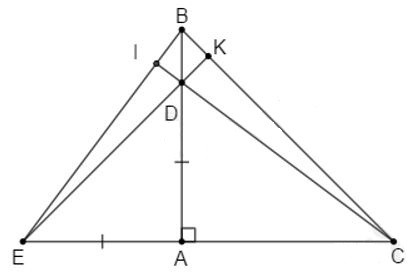
Câu 15: Cho tam giác nhọn ABC có hai đường cao AH và BK cắt nhau tại D
15.1: Biết , tính
A.
B.
C.
D.
Đáp án: A
Giải thích:
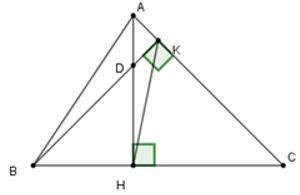
Xét tam giác CHK có (1)
(định lí tổng ba góc trong tam giác)
Xét tam giác DHK có (2)
(định lí tổng ba góc trong tam giác)
Từ (1) và (2) suy ra:
Mà ;
Suy ra:
15.2: Nếu thì tam giác ABC là tam giác
A. Cân tại A
B. Cân tại B
C. Cân tại C
D. Đều
Đáp án: AC
Giải thích:
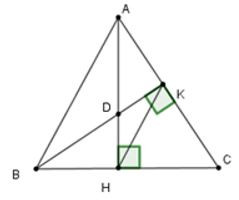
Nếu thì tam giác DAB cân tại D suy ra (1) (tính chất tam giác cân)
Xét tam giác AHB có (2)
Xét tam giác ABK có: (3)
Từ (1)(2)(3) ta suy ra hay suy ra tam giác ABC cân tại C
Câu 16: Cho cân tại A, hai đường cao BD và CE cắt nhau tại I. Tia AI cắt BC tại M. Khi đó là tam giác gì?
A. Tam giác cân
B. Tam giác vuông cân
C. Tam giác vuông
D. Tam giác đều
Đáp án: A
Giải thích:
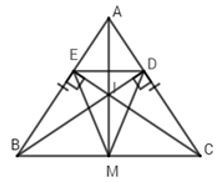
Xét có BD và CE là đường cao cắt nhau tại I suy ra AI là đường cao của tam giác đó
Mà AI cắt BC tại M nên
Vì cân tại A (gt) nên AM là đường cao cũng chính là đường trung trực của tam giác đó (tính chất tam giác cân)
(tính chất đường trung tuyến)
Vì
Xét có M là trung điểm của BC nên suy ra EM là trung tuyến của
(1) (tính chất đường trung tuyến của tam giác vuông)
Xét có M là trung tuyến của BC nên suy ra DM là trung tuyến của
(2) (tính chất đường trung tuyến của tam giác vuông)
Từ (1)(2) cân tại M (dấu hiệu nhận biết tam giác cân)
Các câu hỏi trắc nghiệm Toán lớp 7 có đáp án, chọn lọc khác:
Trắc nghiệm Quan hệ giữa góc và cạnh đối diện trong tam giác có đáp án
Trắc nghiệm Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức trong tam giác có đáp án
Trắc nghiệm Tính chất ba đường trung tuyến trong tam giác có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học 8 có đáp án
- Trắc nghiệm Toán lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn 8 có đáp án
- Trắc nghiệm Hóa học lớp 8 có đáp án
- Trắc nghiệm Địa Lí lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 8 có đáp án
- Trắc nghiệm GDCD lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Vật Lí lớp 8 có đáp án
- Trắc nghiệm Công nghệ lớp 8 có đáp án
- Trắc nghiệm Tin học lớp 8 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Sinh học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Toán lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Hóa học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn lớp 11 có đáp án
- Trắc nghiệm Tiếng Anh lớp 11 có đáp án
- Trắc nghiệm Vật Lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Địa lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm GDCD lớp 11 có đáp án
- Trắc nghiệm Lịch sử lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Công nghệ lớp 11 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 11 có đáp án
- Trắc nghiệm Tin học lớp 11 có đáp án
- Trắc nghiệm Toán lớp 12 có đáp án
- Trắc nghiệm Sinh học lớp 12 có đáp án
- Trắc nghiệm Hóa học lớp 12 có đáp án
- Trắc nghiệm Ngữ văn lớp 12 có đáp án
- Trắc nghiệm Tiếng Anh lớp 12 có đáp án
- Trắc nghiệm Địa lí lớp 12 có đáp án
- Trắc nghiệm Vật Lí lớp 12 có đáp án
- Trắc nghiệm Công nghệ lớp 12 có đáp án
- Trắc nghiệm Giáo dục công dân lớp 12 có đáp án
- Trắc nghiệm Lịch sử lớp 12 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 12 có đáp án
