Trắc nghiệm Quan hệ giữa đường vuông góc và đường xiên. Đường xiên và hình chiếu của đường xiên có đáp án - Toán lớp 7
Bộ 19 bài tập trắc nghiệm Toán lớp 7 Bài 2: Quan hệ giữa đường vuông góc và đường xiên. Đường xiên và hình chiếu của đường xiên có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 7 Bài 2.
Trắc nghiệm Toán 7 Bài 2: Quan hệ giữa đường vuông góc và đường xiên.
Đường xiên và hình chiếu của đường xiên
Bài giảng Trắc nghiệm Toán 7 Bài 2: Quan hệ giữa đường vuông góc và đường xiên.
Đường xiên và hình chiếu của đường xiên
Câu 1: Em hãy chọn phát biểu sai trong các phát biểu sau:
A. Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.
B. Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào có hình chiếu lớn hơn thì lớn hơn
C. Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào lớn hơn thì có hình chiếu nhỏ hơn
D. Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau và ngược lại nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau
Đáp án: C
Giải thích:
Trong các phát biểu ở ý A, B, và D đều đúng.
Ý C sai vì: trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào lớn hơn thì có hình chiếu lớn hơn.
Câu 2: Cho hình vẽ sau:
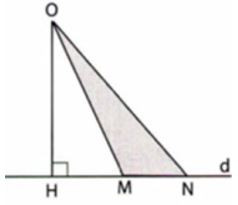
Em hãy chọn khẳng định sai trong các khẳng định sau:
A. OM > OH
B. ON > OH
C. ON > OM
D. ^OMN<^MNO
Đáp án: D
Giải thích:
Vì OH là đường vuông góc và OM, ON là đường xiên nên OH<OM; OH<ON(quan hệ giữa đường vuông góc và đường xiên)
Vì M nằm giữa hai điểm H và N nên HM<HN suy ra OM<ON (quan hệ giữa đường xiên và hình chiếu)
△OHM vuông tại H nên ^HMO là góc nhọn hay ^HMO<90°
Mặt khác: ^HMO+^OMN=180° (hai góc kề bù)
⇒^OMN>180°-90°
⇒^OMN>90° hay ^OMN là góc tù
Xét △OMN có ^OMN là góc tù nên ^OMN>^MNO
Vậy đáp án D sai
Câu 3: Cho góc ^xOy=60°, A là điểm trên tia Ox, B là điểm trên tia Oy (A, B không trùng với O)
Chọn câu đúng nhất
A. OA+OB≤2AB
B. OA+OB=2AB khi OA=OB
C. OA+OB≥2AB
D. Cả A, B đều đúng
Đáp án: D
Giải thích:
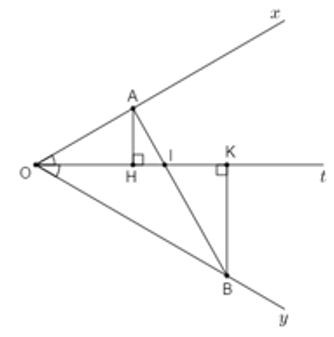
Kẻ tia phân giác Ot của ^xOy nên ^xOt=^yOt=^xOy2=60°2=30°
Gọi I là giao của Ot và AB; H, K lần lần lượt là hình chiếu của A, B trên tia Ot
Xét △OAH có ^AOH=30° nên OA=2AH.
Vì AH, AI lần lượt là đường vuông góc, đường xiên kẻ từ A đến Ot nên AH≤AI do đó OA≤2AI (1)
Xét △OBK có ^BOK=30° nên OB=2BK.
Vì BK, BI lần lượt là đường vuông góc, đường xiêm kẻ từ B đến Ot nên BK≤BI do đó OB≤2BI (2)
Từ (1) và (2) theo vế với vế ta được:
OA+OB≤2AI+2BI=2(AI+BI)=2AB
Dấu "=" xảy ra khi và chỉ lhi H, I, K trùng nhau hay AB⊥Ot nên ^AIO=^BIO=90°
Xét △OAI và △OBI có:
^AIO=^BIO=90°
OI cạnh chung
^AOI=^BOI (vì Ot là tia phân giác của ^xOy)
⇒△OAI=△OBI(g.c.g)
⇒OA=OB(hai cạnh tương ứng)
Vậy OA+OB=2AB hay OA=OB
Câu 4: Trong tam giác ABC có AH vuông góc với BC (H∈BC). Chọn câu sai
A. Nếu AB<AC thì BH<HC
B. Nếu AB>AC thì BH<HC
C. Nếu AB=AC thì BH=HC
D. Nếu BH>HC thì AB>AC
Đáp án: B
Giải thích:
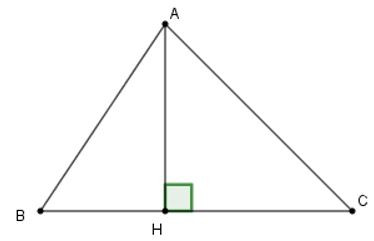
Trong tam giác ABC có AH là đường vuông góc và BH; CH là hai hình chiếu
Khi đó:
+ Nếu AB<AC thì BH<HC (A đúng)
+ Nếu AB>AC thì BH>HC (B sai)
+ Nếu AB=AC thì BH=HC (C đúng)
+ Nếu BH>HC thì AB>AC (D đúng)
Câu 5: Em hãy chọn cụm từ thích hợp điền vào chỗ trống:
"Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào có hình chiếu nhỏ hơn thì ..."
A. lớn hơn
B. ngắn nhất
C. nhỏ hơn
D. bằng nhau
Đáp án: C
Giải thích:
Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào có hình chiếu nhỏ hơn thì nhỏ hơn.
Câu 6: Cho hình vẽ sau:
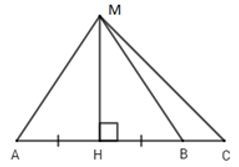
Em hãy chọn đáp án sai trong các đáp án sau:
A. MA > MH
B. HB < HC
C. MA = MB
D. MC < MA
Đáp án: D
Giải thích:
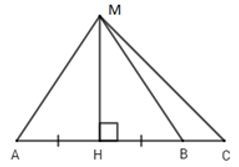
Vì MH là đường vuông góc và MA là đường xiên MA>MH (quan hệ giữa đường vuông góc và đường xiên). Đáp án A đúng nên loại A
Vì ^MBC là góc ngoài của △MHB
⇒^MBC>^MHB=90°
Xét △MBC có: ^MBC là góc tù nên suy ra MB>MC (quan hệ giữa đường vuông góc và cạnh trong tam giác
Mà HB và HC lần lượt là hình chiếu của MB và MC trên AC
⇒HB<HC(quan hệ giữa đường xiên và hình chiếu).
Đáp án B đúng nên loại đáp án B
Vì AH=HB(gt) mà AH và HB lần lượt là hai hình chiếu của AM và BM
⇒MA=MB(quan hệ giữa đường xiên và hình chiếu).
Đáp án C đúng nên loại đáp án C
Ta có: {MB=MA(cmt)MC>MB(cmt)⇒MC>MA.
Đáp án D sai nên chọn đáp án D
Câu 7: Cho △ABC có 90°>ˆB>ˆC. Kẻ AH⊥BC(H∈BC). Gọi M là một điểm nằm giữa H và B, N thuộc tia đối của tia CB
7.1: So sánh HB và HC
A. HB < HC
B. HB = HC
C. HB > HC
D. Cả A,B,C đều sai
Đáp án: A
Giải thích:
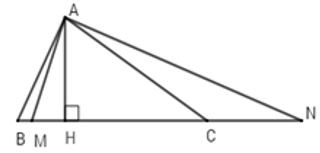
Vì ˆB>ˆC(gt)⇒AC>AB (1) (quan hệ giữa góc và cạnh trong tam giác)
Mà HB, HC tương ứng hình chiếu của AB,AC trên BC
⇒HB<HC (quan hệ giữa đường xiên và hình chiếu)
7.2: Chọn câu sai
A. AM < AB < AN
B. AM > AB >AN
C. AM < AB = AN
D. AM = AB = AN
Đáp án: A
Giải thích:
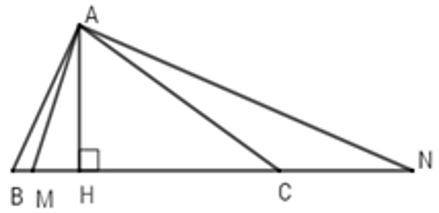
Vì M nằm giữa B và H ⇒HM<HB
Mà HM và HB tương ứng là hình chiếu của AM và AB trên BC
⇒AM<AB (2) (quan hệ giữa đường xiên và hình chiếu)
Vì N thuộc tia đối của tia CB thì suy ra HN>HC. Mà HN và HC tương ứng là hình chiếu của AN và AC trên BC ⇒AC<AN (3) (quan hệ giữa đường xiên và hình chiếu)
Từ (1), (2), (3) ⇒AM<AB<AN
Câu 8: Cho △ABC có CE và BD là đường cao. So sánh BD+CE và AB+AC?
A. BD+CE<AB+AC
B. BD+CE>AB+AC
C. BD+CE≤AB+AC
D. BD+CE≥AB+AC
Đáp án: A
Giải thích:
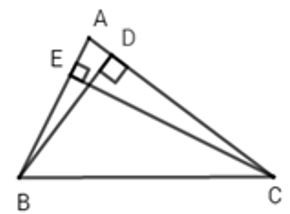
Vì {BD⊥AC(gt)EC⊥AB(gt)
⇒ BD và CE lần lượt là hai đường vuông góc của hai đường xiên AC và AB
⇒{BD<ABEC<AC(đường vuông góc nhỏ hơn đường xiên)
⇒BD+CE<AB+AC
Câu 9: Cho D là một điểm nằm trong △ABC. Nếu AD=AB thì:
A. AB = AC
B. AB > AC
C. AB < AC
D. AB≥AC
Đáp án: C
Giải thích:
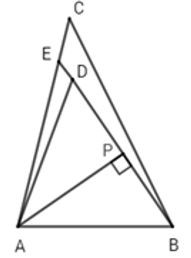
Gọi E là giao điểm BD và AC, kẻ AP⊥BD
Gọi AD=AB (gt) mà PD và BP lần lượt là hình chiếu của AB và AB trên BE
⇒PD=BP (quan hệ giữa đường xiên và hình chiếu)
Do PE>PD=PB nên AE<AD (1).
Mặt khác, AC>AE (2) nên từ (1) và (2)
⇒AC>AB
Câu 10: Cho △ABC có CE và BD là đường vuông góc (E∈AB, D∈AC). So sánh BD+CE và 2BC?
A. BD+CE>2BC
B. BD+CE<2BC
C. BD+CE≤2BC
D. BD+CE=2BC
Đáp án: B
Giải thích:
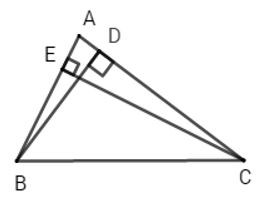
Vì BD và BC lần lượt là đường vuông góc và đường xiên kẻ từ B đến AC nên BD<BC(1)
Vì CE và BC lần lượt là đường vuông góc và đường xiên kẻ từ C đến AB nên CE<BC(2)
Cộng (1) với (2) theo vế với vế ta được:
BD+CE<BC+BC hay BD+CE<2BC
Câu 11: Cho △ABC có ˆC=90°, AC<BC, kẻ CH⊥AB. Trêm các cạnh AB và AC lấy tương ứng hai điểm M và N sao cho BM=BC, CN=CH. Chọn câu đúng nhất
A. MN⊥AC
B. AC+BC<AB+CH
C. Cả A, B đều sai
D. Cả A, B đều đúng
Đáp án: D
Giải thích:
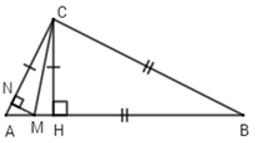
Ta có: BM=BC(gt)⇒△BMC cân tại B (dấu hiệu nhận biết tam giác cân)
⇒^MCB=^CMB (1) (tính chất tam giác cân)
Lại có:
{^BCM+^MCA=^ACB=90°(gt)^CMH+^MCH=90°(gt)
Từ (1) và (2) ⇒^MCH=^MCN
Xét △MHC và △MNC có:
MC chung
^MCH=^MCN(cmt)
NC = HC (gt)
⇒△MHC=△MNC(c.g.c)
⇒^MNC=^MHC=90° (hai góc tương ứng)
⇒MN⊥AC nên A đúng
Xét △AMN có AN là đường vuông góc hạ từ A xuống MN và AM là đường xiên nên suy ra AM>AN (quan hệ đường vuông góc và đường xiên)
Ta có:
{BM=BC(gt)HC=CN(gt)AM>AN(cmt)
⇒BM+MA+HC>BC+CN+NA
Câu 12: Cho △ABC có 90°<ˆA<180°. Trên cạnh AB và AC lấy tương ứng hai điểm M và N (M, N không trùng với các đỉnh của △ABC). Chọn đáp án đúng nhất
A. BA < BN < BC
B. BA > BN >BC
C. CA < CM < CB
D. Cả A,C đều đúng
Đáp án: D
Giải thích:
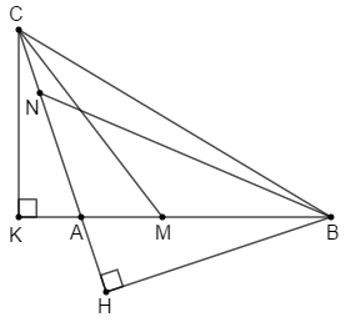
Từ B kẻ BH vuông góc với AC, vì ^BAC là góc tù nên H nằm ngoài đoạn thẳng AC
Khi đó BA, BN, BC là đường xiên kẻ từ B đến AC, HA, HN, HC lần lượt là các hình chiếu của BA, BN, BC trên AC
Ta có: HA<HN<HC nên BA<BN<BC (quan hệ giữa đường xiên và hình chiếu)
Từ C kẻ CK vuông góc với AC, vì ^BAC là góc tù nên K nằm ngoài đoạn thẳng AB
Khi đó CA, CM, CB à các đường xiên kẻ từ C đém AB, AK, KM, KB lần lượt là các hình chiếu của CA, CM, CB trên AB
Ta có: KA<KM<KB nên CA<CM<CB (quan hệ giữa đường xiên và hình chiếu)
Câu 13: Cho △ABC vuông tại A, M là trung điểm của AC. Gọi D, E lần lượt là hình chiếu A và C xuống đường thẳng BM. So sánh BD+BE và AB
A. BD + BE > 2AB
B. BD + BE < 2AB
C. BD + BE = 2AB
D. BE + BE < AB
Đáp án: A
Giải thích:
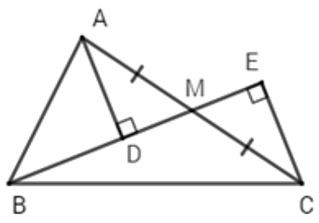
△ABM vuông tại A (gt) nên BA<BM (quan hệ giữa đường vuông góc và đường xiên)
Mà BM=BD+DM⇒BA<BD+DM (1)
Mặt khác: BM=BE-ME⇒BA<BE-ME (2)
Cộng hai vế của (1) và (2) ta được:
2AB<BD+BE+MD-ME(3)
Vì M là trung điểm của AC (gt) ⇒AM=MC (tính chất trung điểm)
Xét tam giác vuông ADM và tam giác vuông CEM có
AM = MC (cmt)
^ADM=^EMC (đối đỉnh)
⇒△ADM=△CEM (cạnh huyền - góc nhọn)
⇒MD=ME (hai cạnh tương ứng)(4)
Từ (3) và (4) ⇒BD+BE>2AB
Câu 14: Cho ba điểm A, B, C thẳng hàng và B nằm giữa A và C. Trên đường thẳng vuông góc với AC tại B ta lấy điểm M. So sánh MB và MC, MB và MA
A. MA < MB; MC > MB
B. MA > MB; MC < MB
C. MA > MB; MC >MB
D. MA < MB; MC < MB
Đáp án: C
Giải thích:
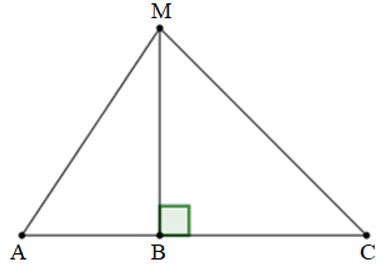
Vì MB là đường vuông góc và MA, MC là đường xiên nên MA>MB; MC>MB(quan hệ giữa đường vuông góc và đường xiên)
Câu 15: Cho △ABC vuông tại A. Trên cạnh AB và AC lấy tương ứng hai điểm D và E (D,E không trùng với các đỉnh của △ABC). Chọn đáp án đúng nhất
A. DE > BE > BC
B. DE < BE < BC
C. DE > BE = BC
D. DE < BE = BC
Đáp án: B
Giải thích:
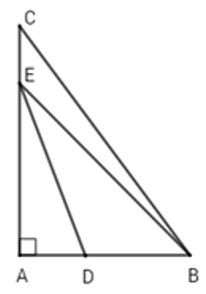
Vì D nằm giữa A và B nên suy ra AD<AB. Mà AD và AB lần lượt là hình chiếu của ED và EB trên AB ⇒ED<EB (1) (quan hệ giữa đường xiên và hình chiếu)
Vì E nằm giữa A và C nên suy ra AE<AC. Mà AE và AC lần lượt là hình chiếu của EB và BC trên AC⇒EB<BC (2) (quan hệ giữa đường xiên và hình chiếu)
Từ (1), (2) ⇒ED<EB<BC
Câu 16: Cho tam giác ABC có chiều cao AH
A. Nếu BH<HC thì AB<AC
B. Nếu AB<AC thì BH<HC
C. Nếu BH=HC thì AB=AC
D. Cả A, B, C đều đúng
Đáp án: D
Giải thích:
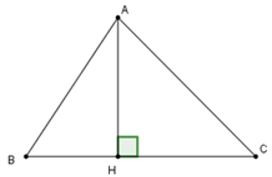
Trong tam giác ABC có AH là đường vuông góc và BH; CH là hai hình chiếu
Khi đó:
+ Nếu BH<HC thì AB<AC
+ Nếu AB<AC thì BH<HC
+ Nếu BH=HC thì AB=AC
Nên A, B, C đều đúng
Câu 17: Cho △ABC vuông tại A, M là trung điểm của AC. Gọi D, E lần lượt là hình chiếu A và C xuống đường thẳng BM. Chọn câu đúng nhất
A. AD+CE<2AB
B. AB+EC<AC
C. AB+EC=AC
D. Cả A, B đều đúng
Đáp án: D
Giải thích:
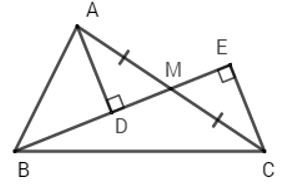
Vì M là trung điểm AC (gt) ⇒AM=MC (tính chất trung điểm)
Xét tam giác ADM và tam giác CEM có:
AM = MC (cmt)
^ADM=^EMC (đối đỉnh)
⇒△ADM=△CEM (cạnh huyền - góc nhọn)
⇒AD=CE (hai cạnh tương ứng)
Xét △ABD vuông tại D nên AD<AB
⇒2AD<2AB⇒AD+AD<2AB hay AD+CE<2AB (A đúng)
△ADM vuông tại D nên AD<AM (1)
△CEM vuông tại E nên EC<CM (2)
Cộng (1) với (2) theo vế với vế ta được:
AD+EC<AM+CM hay AD+EC<AC (B đúng)
Vậy A, B đều đúng
Câu 18: Cho ba điểm A, B, C thẳng hàng và B nằm giữa A và C. Trên đường thẳng vuông góc với AC tại B ta lấy điểm H. Khi đó:
A. AH < BH
B. AH < AB
C. AH > BH
D. AH = BH
Đáp án: C
Giải thích:
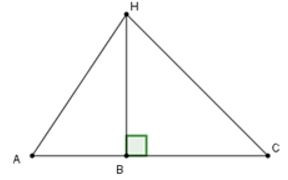
Vì BH là đường vuông góc và AH là đường xiên nên AH>BH
Các câu hỏi trắc nghiệm Toán lớp 7 có đáp án, chọn lọc khác:
Trắc nghiệm Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức trong tam giác có đáp án
Trắc nghiệm Tính chất ba đường trung tuyến trong tam giác có đáp án
Trắc nghiệm Tính chất tia phân giác của một góc có đáp án
Trắc nghiệm Tính chất ba đường phân giác của tam giác có đáp án
Trắc nghiệm Tính chất đường trung trực của một đoạn thẳng có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học 8 có đáp án
- Trắc nghiệm Toán lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn 8 có đáp án
- Trắc nghiệm Hóa học lớp 8 có đáp án
- Trắc nghiệm Địa Lí lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 8 có đáp án
- Trắc nghiệm GDCD lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Vật Lí lớp 8 có đáp án
- Trắc nghiệm Công nghệ lớp 8 có đáp án
- Trắc nghiệm Tin học lớp 8 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Sinh học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Toán lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Hóa học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn lớp 11 có đáp án
- Trắc nghiệm Tiếng Anh lớp 11 có đáp án
- Trắc nghiệm Vật Lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Địa lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm GDCD lớp 11 có đáp án
- Trắc nghiệm Lịch sử lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Công nghệ lớp 11 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 11 có đáp án
- Trắc nghiệm Tin học lớp 11 có đáp án
- Trắc nghiệm Toán lớp 12 có đáp án
- Trắc nghiệm Sinh học lớp 12 có đáp án
- Trắc nghiệm Hóa học lớp 12 có đáp án
- Trắc nghiệm Ngữ văn lớp 12 có đáp án
- Trắc nghiệm Tiếng Anh lớp 12 có đáp án
- Trắc nghiệm Địa lí lớp 12 có đáp án
- Trắc nghiệm Vật Lí lớp 12 có đáp án
- Trắc nghiệm Công nghệ lớp 12 có đáp án
- Trắc nghiệm Giáo dục công dân lớp 12 có đáp án
- Trắc nghiệm Lịch sử lớp 12 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 12 có đáp án
