Nội dung bài viết

    Xem thêm

    Cho tam giác ABC cân tại A.Trên cạnh AB lấy điểm M, trên tia đối của tia CA lấy điểm N

    Vietjack.me giới thiệu bộ câu hỏi ôn tập Toán có đáp án được biên soạn bám sát chương trình học giúp bạn ôn luyện và bổ sung kiến thức môn Toán tốt hơn. Mời các bạn đón xem:

    1 1,323 02/02/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Cho tam giác ABC cân tại A.Trên cạnh AB lấy điểm M, trên tia đối của tia CA lấy điểm N

    Đề bài: Cho ΔABC cân tại A.Trên cạnh AB lấy điểm M, trên tia đối của tia CA lấy điểm N sao cho AM + AN = 2AB.

    a) Chứng minh rằng: BM = CN

    b) Chứng minh rằng: BC đi qua trung điểm của đoạn thẳng MN.

    c) Đường trung trực của MN và tia phân giác của BAC^ cắt nhau tại K. Chứng minh rằng ΔBKM = ΔCKN từ đó suy ra KC vuông góc với AN

    Lời giải:

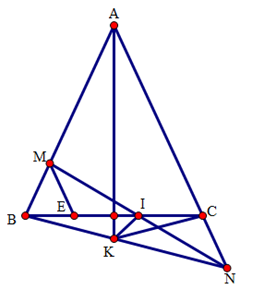
    Tài liệu VietJack

    a) Do tam giác ABC cân tại A, suy ra AB = AC.

    Ta có: AM + AN = AB – BM + AC + CN = 2AB – BM + CN.

    Ta lại có AM + AN = 2AB (gt), nên suy ra

    2AB – BM + CN = 2AB ⇔ – BM + CN = 0  ⇔ BM = CN.

    Vậy BM = CN (đpcm).

    b) Gọi I là giao điểm của MN và BC.

    Qua M kẻ đường thẳng song song với AC cắt BC tại E.

    Do ME // NC nên ta có:

    MEB^=ACB^ (hai góc đồng vị) nên ∆BME cân tại M ⇒ BM = ME mà BM = CN nên ME = CN.

    CNI^ = IME^ (hai góc so le trong)

    MEI^ = NCI^ (hai góc so le trong)

    Ta chứng minh được ΔMEI = ΔNCI  (g . c . g)

    Suy ra MI = NI (hai cạnh tương ứng), từ đó suy ra I là trung điểm của MN.

    c) Xét hai tam giác MIK và NIK có:

    MI = IN (cmt),

    MIK^ = NIK^ = 900

    IK là cạnh chung. Do đó ΔMIK = ΔNIK(c.g.c)

    Suy ra KM = KN (hai cạnh tương ứng).

    Xét hai tam giác ABK và ACK có: AB = AC(gt), BAK^ = CAK^ (do BK là tia phân giác của BAC^), AK là cạnh chung, do đó   

    Suy ra KB = KC (hai cạnh tương ứng).

    Xét hai tam giác BKM và CKN có: MB = CN, BK = KN, MK = KC, do đó

    ΔBKM = ΔCKN(c . c . c) suy ra MBK^ = KCN^.

    Mà MBK^ = ACK^⇒ACK^ = KCN^ = 1800 : 2 = 900⇒KC⊥AN.  (đpcm)

    Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:

    Cho tam giác ABC cân tại A.Trên cạnh AB lấy điểm M, trên tia đối của tia CA lấy điểm N...

    Tính bằng cách thuận tiện nhất: 34 000 : 125 : 8...

    Tính: 372,95 : 3...

    Phân tích thành nhân tử 5(x + 3y) - 15x ( x + 3y...

    Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là các điểm đối xứng...

    Cho tam giác ABC có A(5; 3); B(2; -1) và C(-1; 5). Tính tọa độ chân đường cao vẽ từ A...

    Cho tam giác ABC có AB = 3; AC = 5...

    Cho tam giác ABC có AB = 6cm, AC = 3cm...

    Cho tam giác ABC có trọng tâm G. Các điểm D, E, F lần lượt là trung điểm của BC, CA, AB...

    Số lớn nhất có 4 chữ số khác nhau và tích các chữ số bằng 24 là...

    Giải phương trình: x + x / (căn x^2 - 1) = 35/12...

    Cho a/b = c/d. Chứng minh (2a - 3b)/(2a + 3b) = (2c - 3d)/(2c + 3d)...

    Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O...

    Cho hình chóp S.ABCD có đáy là hình bình hành ABCD với O là giao điểm...

    Cho hình chóp S.ABCD có đáy ABCD là hình bình hành...

    Cho hình thang vuông ABCD có góc A = góc D = 90 độ...

    Cho tam giác ABC nhọn. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC...

    Cho tam giác ABC vuông tại A; đường phân giác BE...

    Cho tam giác ABC vuông tại A điểm M thuộc cạnh BC từ M vẽ các đường thẳng vuông góc...

    Cho tứ giác ABCD có AC cắt BD tại O, góc ABD = góc ACD...

    Anh Long đi taxi từ nhà đến ga tàu hết 35.000 đồng...

    Cho hình bình hành ABCD. Chứng minh rằng với mọi điểm M, ta có...

    Chứng minh với mọi x thuộc N, x^2 + 1 không chia hết cho 3...

    Tổng 2 số lẻ là 884. Tìm 2 số, biết rằng giữa chúng có 7 số chẵn liên tiếp nữa...

    Tìm hai số lẻ biết tổng của chúng là 50 và giữa chúng có ba số lẻ khác...

    Cho nửa đường tròn (O) đường kính AB = 2R. Vẽ đường thẳng d là tiếp tuyến...

    Cho đường tròn tâm O bán kính R và một đường thẳng d cố định không giao nhau...

    Một vật hình hộp chữ nhật có kích thước 30 . 20 . 10...

    Một hình hộp chữ nhật có chiều dài 20 cm, chiều rộng 15 cm, chiều cao 10 cm...

    Tìm số nguyên tố p sao cho p + 8 và p + 16  đều là các số nguyên tố...

    Công thức tính số tổ hợp là...

    Phân tích đa thức thành nhân tử: x^8 + x^7 + 1...

    Gọi  a, b, c lần lượt là ba cạnh của tam giác; ha, hb, hc lần lượt là các đường cao...

    Phân tích đa thức x^5 + x + 1 thành nhân tử...

    Ông và bà An cùng có 6 đứa con đang lên máy bay theo một hàng dọc...

    Tìm số nguyên tố x, y thỏa mãn x^2 – 2y^2 = 1...

    Tổng tất cả các ước của 4 là...

    Tìm x, biết: 4x^2 – 25 – (2x – 5)(2x + 7) = 0...

    Tìm x biết 8x^3 – 12x^2 + 6x – 1 = 0...

    Tìm giá trị y thỏa mãn 49(y – 4)^2 – 9(y + 2)^2 = 0...

    Rút gọn: A = x(5x – 3) – x^2(x – 1) + x(x^2 – 6x) – 10 + 3x...

    Cho hai tập hợp khác rỗng: A = (m – 1; 4], B = (−2; 2m + 2...

    Phân tích đa thức thành nhân tử: A = ab(a + b) – bc(b + c) + ac (a – c...

    Cho x, y, z > 0 thỏa mãn x + y + z = 1. Tìm giá trị lớn nhất của...

    Cho tam giác ABC có P là trung điểm của AB và hai điểm M, N thỏa các hệ thức...

    Phân tích đa thức thành nhân tử: (ab – 1)^2 + (a + b)^2...

    Tính A = 1.2 + 2.3 + 3.4 +…+ n(n + 1...

    Khổ giấy A1 lớn gấp bao nhiêu lần khổ giấy A3...

    Cho hai hàm số y = x^2 và y = mx + 4, với m là tham số...

    Cho hai tập hợp khác rỗng A = (m – 1; 4]; B = (−2; 2m + 2...

    Tìm tất cả số tự nhiên x, y sao cho 2^x + 5^y là số chính phương...

    Một bó hoa 12 bông gồm: 5 hoa hồng, 4 hoa lan còn lại là hoa cúc...

    Trong khai triển (x – 2)^100 = a0 + a1x^1 + … + a100x^100...

    Tính tổng min và max của hàm số y = căn 2+x + căn 2-x ...

    Hình lăng trụ có thể có số cạnh nào sau đây...

    Phân tích đa thức thành nhân tử x^2 + 5x – 6...

    Công thức tính diện tích tam giác đều cạnh a...

    Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau...

    Cho đồ thị hàm số y = f(x) có đồ thị là đường cong trong hình bên...

    Tìm số nguyên tố p để p + 2 và p + 10 cũng là số nguyên tố...

    Tham khảo các loạt bài Toán khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,323 02/02/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: