Cho hình chóp S.ABCD có đáy là hình bình hành. Các điểm I, J lần lượt là trọng tâm
Vietjack.me giới thiệu bộ câu hỏi ôn tập Toán có đáp án được biên soạn bám sát chương trình học giúp bạn ôn luyện và bổ sung kiến thức môn Toán tốt hơn. Mời các bạn đón xem:
Cho hình chóp S.ABCD có đáy là hình bình hành. Các điểm I, J lần lượt là trọng tâm
Đề bài: Cho hình chóp S.ABCD có đáy là hình bình hành. Các điểm I, J lần lượt là trọng tâm tam giác SAB, SAD. Gọi M là trung điểm của CD. Tìm giao điểm E của SD và mặt phẳng IJM.
Lời giải:
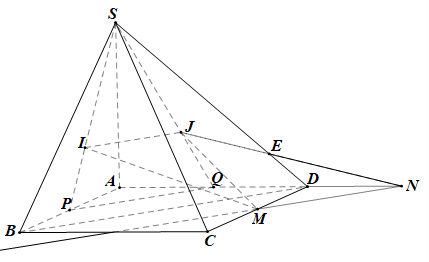
Gọi P, Q lần lượt là trung điểm của AB, AD.
Khi đó PQ là đường trung bình của tam giác ABD nên PQ // BD.
Do I, J lần lượt là trọng tâm tam giác SAB, SAD nên .
Do đó IJ // PQ, suy ra IJ // BD
Có IJ // BD, IJ ⊂ (IJM), BD ⊂ (ABCD)
Þ giao tuyến của (IJM) và (ABCD) là đường thẳng qua M và song song với BD.
Đường thẳng này cắt AD tại N.
Khi đó mp(IJM) chính là mp (IJNM), mp(SAD) chính là mp(SAN)
Trong mp(SAN), JN cắt SD tại E.
Ta có: JN ∩ SD = {E}; JN ⊂ (IJM)
Khi đó E là giao điểm của SD và (IJM).
Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:
Giải phương trình 4sin^2x + 4sinx – 3 = 0...
Cho (d): y = mx – 2 và (P): y = –x^2...
Cho đường thẳng (d): y = 2x + m và parabol (P): y = x^2. Tìm m để (d) cắt (P) tại hai...
Từ 15 học sinh ưu tú của một lớp có bao nhiêu cách...
Tính B = x^5 – 15x^4 + 16x^3 – 29x^2 + 13x tại x = 14...
Cho parabol (P): y = x2 và đường thẳng (d): y = 2x – m (m là tham số...
Tìm giá trị nhỏ nhất của A = 2x^2 – 8x + 1...
Tìm giá trị nhỏ nhất của A(x) = x^2 – 4x + 24...
Một mảnh đất hình chữ nhật có chiều dài 36 m, chiều rộng bằng...
Cho A = (–vô cùng; –2], B = [3; +vô cùng) và C = (0; 4...
Có bao nhiêu số tự nhiên có 3 chữ số được lập từ sáu chữ số 1; 2; 3; 4; 5; 6...
Hình lăng trụ có đáy là thập giác lồi có bao nhiêu cạnh...
Tìm m để đường thẳng y = 2x – 1 và y = 3x + m cắt nhau tại một điểm nằm trên...
Cho hình chóp S.ABCD có đáy là hình bình hành. Các điểm I, J lần lượt là trọng tâm...
Hiệu 2 số là 66,8. Nếu dịch dấu phẩy của số bé sang trái một hàng thì hiệu mới là...
Rô-bốt có hai cái cốc loại 250 ml và 400 ml. Chỉ dùng hai cái cốc đó, làm thế nào để...
Cho 2 tập khác rỗng A = (m – 1; 4]; B = (–2; 2m + 2...
Tìm số tự nhiên a, b biết ƯCLN(a, b) = 4 và a + b = 48...
Đơn giản biểu thức sau khi bỏ ngoặc: a) –a – (b – a – c...
Đơn giản biểu thức sau khi bỏ dấu ngoặc: a) (a + b – c) – (b – c + d...
Cho 3x^2 + 3y^2 = 10xy với y > x > 0. Tính giá trị của biểu thức...
Giải phương trình 5sin^2x + 3sinxcosx – 4cos^2x = 2...
Cho các tập hợp A = {x thuộc R sao cho x nhở hơn bằng a...
Tìm số tự nhiên n để giá trị biểu thức sau là số nguyên tố: A = n^3 – 4n^2 + 4n – 1...
Cho hai tập hợp X = (0; 3] và Y = (a; 4). Tìm tất cả các giá trị của a...
Tìm x biết: x^4 + 2x^3 – 6x – 9 = 0...
Giải phương trình cos2x – 3cosx + 2 = 0...
Giải phương trình lượng giác: sin^2 2x + sin^2 4x = sin^2 6x...
Giải phương trình sau: sin^2 2x = 1/2...
Cho mười chữ số 0, 1, 2, 3, …, 9. Có bao nhiêu số tự nhiên lẻ gồm 6 chữ số khác...
Tìm tổng của số lẻ nhỏ nhất có ba chữ số khác nhau với số chẵn lớn nhất gồm 2...
Tính tổng sau: 1 + 2 + 3 + … + 99...
Giải phương trình: x^3(x^2 – 7)^2 – 36x = 0...
Tìm giá trị lớn nhất và nhỏ nhất của biểu thức: a) A = cos^4x – cos^2x + sin^2x...
Cho các đa thức sau: A = x^3 + 4x^2 + 3x – 7 và B = x + 4...
Khi nhân một số với 39, một học sinh đã đặt nhầm các tích riêng thẳng cột nên tìm ra...
May 13 chiếc áo hết 19,5 m vải, may 12 cái quần hết 12,6 m. Hỏi may bộ quần áo hết...
Một ô tô cứ đi 100 km thì tiêu thụ hết 12,5 lít xăng. Hỏi ô tô đó đi quãng đường dài...
Thương của hai số bằng 468. Nếu giữ nguyên số bị chia và số chia gấp lên 18 lần thì...
Tổng của tất cả các số nguyên a mà –7 < a ≤ 7 bằng bao nhiêu...
Trong 4 giờ xe máy đi được 121 km, trong 2 giờ ô tô đi được 111 km...
Tìm hai số biết tổng của hai số đó là 102,1. Nếu số thứ nhất gấp 5 lần và giữ nguyên...
Tìm x, biết: 35,8 + x × 4 = 100...
Tìm x: (x – 12) – 15 = 20 – (17 + x...
Tìm x, biết: 5.(12 – x) – 20 = 30...
Một hồ bơi dạng hình hộp chữ nhật có kích thước trong lòng hồ là: Chiều dài 12m...
Trong phép tính 121,23 : 14 và có thương là 8,65, vậy số dư là bao nhiêu...
Xem thêm các chương trình khác:
- Các dạng bài tập Tiếng Anh thông dụng nhất
- 3000 câu hỏi ôn tập môn Tiếng Anh có đáp án
- Toàn bộ kiến thức về cụm động từ | Định nghĩa và cách dùng
- 500 đoạn văn Tiếng Anh thông dụng nhất và cách làm
- 1000 câu hỏi ôn tập môn Công nghệ có đáp án
- 1000 câu hỏi ôn tập Giáo dục công dân
- 3000 câu hỏi ôn tập môn Vật lí có đáp án
- Tổng hợp Dạng bài - Công thức môn Vật lí
- Phương trình hóa học | Tổng hợp PTHH của các chất hữu cơ, vô cơ chính xác nhất
- Đồng phân & Công thức cấu tạo của các chất hữu cơ
- Nhận biết các chất Hóa học
- Cấu hình electron
- So sánh bán kính nguyên tử và bán kính ion
- 1000 câu hỏi ôn tập môn Hóa có đáp án
- Wiki các chất hóa học | Định nghĩa, tính chất, nhận biết, điều chế, ứng dụng
- Cách đọc danh pháp hóa học (chương trình mới) đầy đủ nhất
- Công thức Lewis của một số chất thường gặp (chương trình mới)
- Công thức electron của một số chất thường gặp (chương trình mới)
- Công thức cấu tạo của một số chất thường gặp (chương trình mới)
- Công thức hợp chất khí với hidro của các nguyên tố (phổ biến) | Cách viết công thức hợp chất khí với hidro
- Công thức hidroxit cao nhất của các nguyên tố (phổ biến) | Cách viết công thức hidroxit cao nhất
- Công thức oxit cao nhất của các nguyên tố (phổ biến) | Cách viết công thức oxit cao nhất
- 2000 câu hỏi ôn tập môn Tin học có đáp án
- 3000 câu hỏi ôn tập môn Lịch sử có đáp án
- 3000 câu hỏi ôn tập môn Địa lí có đáp án
- 2000 câu hỏi ôn tập môn Sinh học có đáp án
- Tổng hợp Dạng bài - Công thức môn Sinh học
- Tổng hợp về các tác giả văn học
- 3000 câu hỏi ôn tập môn Ngữ văn có đáp án
- Tổng hợp kiến thức Ngữ Văn
- Trò chơi Powerpoint | Game Powerpoint
- Tổng hợp bài thu hoạch BDTX Giáo viên mầm non (2024) theo Thông tư 12
- Tổng hợp bài thu hoạch BDTX Giáo viên tiểu học (2024)
- Tổng hợp bài thu hoạch BDTX Giáo viên THCS (2024)
- Tổng hợp bài thu hoạch BDTX Giáo viên THPT (2024)
