Nội dung bài viết

    Xem thêm

    Cho đường tròn (O) và một điểm M nằm ngoài đường tròn. Từ M kẻ hai tiếp tuyến

    Vietjack.me giới thiệu bộ câu hỏi ôn tập Toán có đáp án được biên soạn bám sát chương trình học giúp bạn ôn luyện và bổ sung kiến thức môn Toán tốt hơn. Mời các bạn đón xem:

    1 286 13/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Cho đường tròn (O) và một điểm M nằm ngoài đường tròn. Từ M kẻ hai tiếp tuyến

    Đề bài: Cho đường tròn (O) và một điểm M nằm ngoài đường tròn. Từ M kẻ hai tiếp tuyến MA, MB với đường tròn (O) (A và B là hai tiếp điểm). Gọi I là giao điểm của OM và AB. Kẻ đường kính BC của (O). Chứng minh OI.OM = OA2

    *Lời giải:

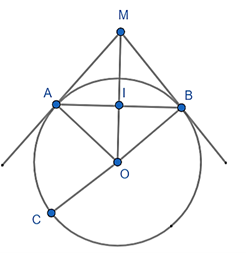
    Tài liệu VietJack

    Ta có: OA = OB (bán kính)

    MA = MB (tính chất hai tiếp tuyến cắt nhau)

    ⇒ OM là trung trực của AB ⇒ OM ⊥ AB tại I.

    ΔOAM vuông tại A đường cao AI

    ⇒ OI.OM = OA2 (hệ thức giữa cạnh và đường cao).

    *Phương pháp giải:

    - Áp dụng tính chất hai tiếp tuyến cắt nhau của đường tròn:

    Định lí: Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:

    • Điểm đó cách đều hai tiếp điểm.

    • Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.

    • Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.

    *Lý thuyến cần nắm và dạng toán về tiếp tuyến đường tròn:

    Dấu hiệu nhận biết tiếp tuyến của đường tròn

    Một đường thẳng là tiếp tuyến của đường tròn khi nó đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó.

    Chú ý: Ta có các tính chất của tiếp tuyến như sau:

    • Tiếp tuyến của đường tròn vuông góc với bán kính tại tiếp điểm.

    • Khoảng cách từ tâm của đường tròn đến tiếp tuyến luôn bằng bán kính của đường tròn đó.

    Tính chất của hai tiếp tuyến cắt nhau

    Định lí: Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:

    • Điểm đó cách đều hai tiếp điểm.

    • Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.

    • Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.

    Đường tròn nội tiếp tam giác

    - Đường tròn tiếp xúc với ba cạnh của một tam giác gọi là đường tròn nội tiếp tam giác, còn tam giác gọi là tam giác ngoại tiếp đường tròn.

    - Tâm của đường tròn nội tiếp tam giác là giao của ba đường phân giác các góc trong tam giác.

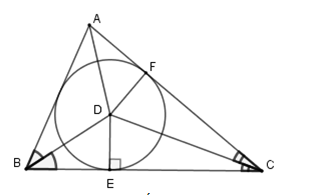
    Các dạng bài toán về tiếp tuyến của đường tròn và cách giải – Toán lớp 9 (ảnh 1)

    Cho tam giác ABC có D là giao của ba đường phân giác nên D là tâm đường tròn nội tiếp tam giác.

    Khi đó D cách đều ba cạnh tam giác.

    Đường tròn bàng tiếp tam giác

    - Đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với phần kéo dài của hai cạnh tam giác còn lại thì gọi là đường tròn bàng tiếp tam giác.

    - Với mỗi tam giác, ta xác định được ba đường tròn bàng tiếp.

    - Tâm của đường tròn bàng tiếp tam giác được xác định bởi giao của hai đường phân giác góc ngoài của hai đỉnh tạo thành cạnh mà đường tròn tiếp xúc.

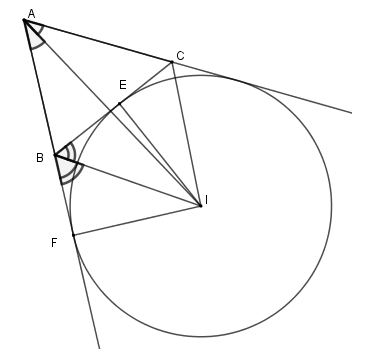
    Các dạng bài toán về tiếp tuyến của đường tròn và cách giải – Toán lớp 9 (ảnh 1)

    Cho tam giác ABC có I là giao của hai đường phân giác ngoài góc B và góc C nên I là tâm đường tròn bàng tiếp tam giác.

    Dạng 1: Chứng minh một đường thẳng là tiếp tuyến của một đường tròn

    Phương pháp giải: Để chứng minh một đường thẳng a là tiếp tuyến của đường tròn (O;R) tại điểm C ta làm như sau:

    Cách 1: Chứng minh điểm C thuộc (O) và a vuông góc với OC tại C.

    Cách 2: Kẻ OH vuông góc với a tại H. Chứng minh OH = OC = R.

    Cách 3: Vẽ tiếp tuyến a’ của (O;R) tại C. Chứng minh a trùng a’.

    Dạng 2: Tính độ dài

    Phương pháp giải:Nối tâm với tiếp điểm rồi vận dụng tính chất của tiếp tuyến và sử dụng các công thức về hệ thức lượng trong tam giác vuông.

    Dạng 3: Chứng minh hai đường thẳng bằng nhau, hai đường thẳng song song, hai đường thẳng vuông góc

    Phương pháp giải: Dùng tính chất tiếp tuyến, hai tiếp tuyến cắt nhau.

    Dạng 4: Chứng minh tiếp tuyến, tính độ dài, số đo góc dựa vào tính chất hai tiếp tuyến cắt nhau

    Phương pháp giải: Chúng ta sử dụng các nội dung kiến thức sau

    - Tính chất hai tiếp tuyến cắt nhau

    - Khái niệm đường tròn nội tiếp, đường tròn bàng tiếp tam giác

    - Các hệ thức lượng trong tam giác vuông

    Xem thêm các bài viết liên quan hay, chi tiết

    Lý thuyết Tiếp tuyến của đường tròn - Toán 9 Chân trời sáng tạo

    50 Bài tập Dấu hiệu nhận biết tiếp tuyến của đường tròn Toán 9 mới nhất

    Toán 9 Bài 3 giải vở bài tập (Cánh diều): Tiếp tuyến của đường tròn

    Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:

    Tìm số lớn nhất có 4 chữ số khác nhau, chữ số hàng trăm là chữ số 5. Số này phải...

    Tìm x, y thỏa mãn 2x^2 + y^2 + 9 = 6x + 2xy...

    Tổ 1 và tổ 2 chăm sóc 28500 m2 rừng. Sau khi chuyển 2500 m2 rừng của tổ 1 sang tổ...

    Các số thực a,b,c,d thỏa mãn đồng thời các điều kiện abc – d = 1, bcd – a = 2, cda – b...

    Cho dãy số (un) có u1 = 4 và un+1 = 3un – 2. Tìm số hạng thứ 5 của dãy...

    Tìm số hạng đầu tiên của cấp số nhân, biết rằng công bội là 3, tổng các số hạng là 728...

    Một người bán 120kg gạo, trong đó có 65% là gạo tẻ, còn lại là gạo nếp. Hỏi người...

    Bác Vinh mua 1425 viên gạch bông để lát nền nhà. Bác dự tính sẽ thừa ra 125 viên đủ...

    Cho các chữ số 0;1;2;3;4;5. Từ các chữ số này ta có thể lập được bao nhiêu số có 3...

    Một biển báo giao thông như hình vẽ. Tính diện tích phần tô đậm của biển báo, biết...

    Một cấp số cộng (un) có u9 = 47; công sai d = 5. Số 10092 là số hạng thứ mấy trong...

    Một người nuôi ong thu hoạch được 40 lít mật ong. người đó muốn đổ vào các chai...

    Tuần này lớp 6A và 6B gồm 40 học sinh nữ và 36 học sinh nam được phân công đi...

    Tìm số dư trong phép chia 0,6159 : 0,52 ( số thương chỉ lấy đến hai chữ số ở phần...

    Tìm x biết: x(x + 2)(x^2 + 2x + 2) + 1 = 0...

    5,34 km2 = …ha...

    Diện tích hình vuông tăng lên gấp 4 lần, hỏi độ dài mỗi cạnh hình vuông tăng lên gấp...

    Năm nay bố 32 tuổi và gấp 4 lần tuổi con. Hỏi sau 4 năm nữa tuổi bố gấp mấy lần...

    Sắp xếp 6 nam sinh và 5 nữ sinh vào một dãy ghế hàng ngang có 11 chỗ ngồi. Hỏi có...

    Tìm x để 3 số: 1 − x, x^2, 1 + x theo thứ tự lập thành một cấp số cộng...

    Tính diện tích hình thang có tổng đọ dài của chiều cao và đáy bé bằng 28,7 dm, 3 lần...

    Tính diện tích phần tô đậm biết AB = 16 cm...

    Tính nhanh 1152 – (374 + 1152) + (–65 + 374...

    Một người mua 600 cái bát khi chuyên chở đã có 69 cái bát bị vỡ mỗi cái bát còn lại...

    Biết chu vi của hình chữ nhật là 26m và tỉ số hai cạnh là 1,6. Hỏi diện tích của hình...

    Giá niêm yết một bộ quần áo thể thao tại một cửa hàng A là 780000 đồng...

    Tam giác thường có cạnh huyền không...

    Theo kế hoạch hai tổ sản xuất 600 sản phẩm trong một thời gian nhất định...

    Bài toán Ủng hộ miền Trung năm 2020: Một chuyến hàng ủng hộ miền Trung có 300...

    Cho a + b + c = 0. Chứng minh a^3 + b^3 + c^3 = abc...

    Cho hàm số y = (m – 2)x + m + 1 (d) a) Với giá trị nào của m thì hàm số đã cho là hàm số bậc nhất...

    Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của BC, BD. (P) là mp qua IJ và...

    Một cái lều hình vuông được dựng ở trung tâm của một mảnh vườn hình vuông...

    Một mảnh đất hình chữ nhật có chiều dài 26m, chiều rộng bằng...

    Một lớp học gồm 16 nam và 24 nữ. Muốn chia thành các tổ sao cho số nam, số nữ ở...

    Sau khi xem bảng báo giá ở siêu thị, mẹ bạn Tín đưa cho bạn 1200000 đồng nhờ bạn...

    Sân bóng đá tại trung tâm thể thao quần Tây Hồ là một hình chữ nhật có chiều dài là...

    1. Xây dựng các học liệu số phục vụ cho một hoạt động học trong kế hoạch bài dạy...

    Diện tích bề mặt Trái đất có bao nhiêu ki lô mét vuông...

    Tìm góc tạo bởi đường thẳng y = 2x – 1 với trục Ox...

    Tính tổng S = 1 + 2 + 3 + ... + n...

    Tổng số học sinh của 1 trường THCS là 600 em học sinh. Tính số học sinh mỗi khối...

    Từ các số 0, 1, 2, 7, 8, 9 lập được bao nhiêu số chẵn có năm chữ số khác nhau...

    Vào tháng 5, giá niêm yết một cái tủ lanh tại một siêu thị điện máy là 10000000 đồng...

    Để lát nền một căn phòng người ta đã sử dụng hết 200 viên gạch hình vuông có cạnh...

    Cho x – y = 1. Chứng minh x^3 – y^3 = 1 + 2xy...

    Cho đường tròn (O) và một điểm M nằm ngoài đường tròn. Từ M kẻ hai tiếp tuyến...

    Có 10 quả cầu đỏ được đánh số từ 1 đến 10, 7 quả cầu xanh được đánh số từ 1 đến 7...

    Tăng cạnh hình vuông thêm 25 % ta được một hình vuông mới có chu vi là 15 cm...

    Trong điều kiện thích hợp (khoảng 40 độ C) một con vi khuẩn trong không khí cứ 20...

    Tham khảo các loạt bài Toán khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 286 13/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: