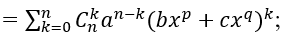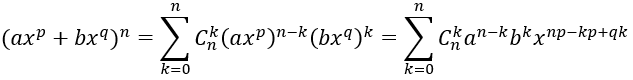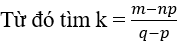Nội dung bài viết

    Xem thêm

    Tìm hệ số của x^15 trong khai triển (x^2 + 8)^12

    Vietjack.me giới thiệu bộ câu hỏi ôn tập Toán có đáp án được biên soạn bám sát chương trình học giúp bạn ôn luyện và bổ sung kiến thức môn Toán tốt hơn. Mời các bạn đón xem:

    1 429 16/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Tìm hệ số của x15 trong khai triển (x2 + 8)12

    Đề bài: Tìm hệ số của x15 trong khai triển (x2 + 8)12.

    Lời giải:

    (x2 + 8)12 = ∑k=012C12k.x2k.812−k .

    Ta thấy (x2)k luôn có số mũ chẵn do đó không xuất hiện x15 trong khai triển này.

    *Phương pháp giải:

    Xác định hệ số của số hạng chứa xm trong khai triển P(x) = (a + bxp + cxq)n

    P(x) = (a + bxp + cxq)n được viết dưới dạng a0 + a1x + ...+ a2nx2n

    Ta làm như sau:

    * Viết P(x) = (a + bxp + cxq)n Chuyên đề Toán lớp 11 | Chuyên đề: Lý thuyết - Bài tập Toán 11 có đáp án

    * Viết số hạng tổng quát khi khai triển các số hạng dạng (bxp+cxq)k thành một đa thức theo luỹ thừa của x.

    * Từ số hạng tổng quát của hai khai triển trên ta tính được hệ số của xm.

    Chú ý: Để xác định hệ số lớn nhất trong khai triển nhị thức Niutơn

    Ta làm như sau:

    * Tính hệ số ak theo k và n;

    * Giải bất phương trình ak-1 ≤ ak với ẩn số k;

    * Hệ số lớn nhất phải tìm ứng với số tự nhiên k lớn nhất thoả mãn bất phương trình trên.

    *Lý thuyết:

    Chuyên đề Toán lớp 11 | Chuyên đề: Lý thuyết - Bài tập Toán 11 có đáp án

    Số hạng chứa xm ứng với giá trị k thỏa mãn: np – pk + qk = m.

    Chuyên đề Toán lớp 11 | Chuyên đề: Lý thuyết - Bài tập Toán 11 có đáp án

    Vậy hệ số của số hạng chứa xm là: 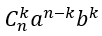Chuyên đề Toán lớp 11 | Chuyên đề: Lý thuyết - Bài tập Toán 11 có đáp án với giá trị k đã tìm được ở trên.

    Nếu k không nguyên hoặc k > n thì trong khai triển không chứa xm , hệ số phải tìm bằng 0.

    Chú ý: Xác định hệ số của số hạng chứa xm trong khai triển P(x) = (a + bxp + cxq)n

    P(x) = (a + bxp + cxq)n được viết dưới dạng a0 + a1x + ...+ a2nx2n

    Ta làm như sau:

    * Viết P(x) = (a + bxp + cxq)n Chuyên đề Toán lớp 11 | Chuyên đề: Lý thuyết - Bài tập Toán 11 có đáp án

    * Viết số hạng tổng quát khi khai triển các số hạng dạng (bxp+cxq)k thành một đa thức theo luỹ thừa của x.

    * Từ số hạng tổng quát của hai khai triển trên ta tính được hệ số của xm.

    Chú ý: Để xác định hệ số lớn nhất trong khai triển nhị thức Niutơn

    Ta làm như sau:

    * Tính hệ số ak theo k và n;

    * Giải bất phương trình ak-1 ≤ ak với ẩn số k;

    * Hệ số lớn nhất phải tìm ứng với số tự nhiên k lớn nhất thoả mãn bất phương trình trên.

    Xem thêm

    Công thức tìm hệ số trong khai triển nhị thức Niu-tơn chi tiết nhất - Toán lớp 11

    Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:

    Điền vào chỗ trống: 789g = …kg...

    Tìm x biết: 6x^2 – (2x – 3)(3x + 2) – 1 = 0...

    Tính tổng A = 3 + 6 + 12 + 24 + … + 3072...

    Chứng minh rằng: A = n^3 + (n+1)^3 + (n+2)^3 chia hết cho 9 với mọi n thuộc...

    Một nhà máy sản xuất sản phẩm với 40% sản phẩm loại I, 50% sản phẩm loại II...

    Một chiếc thuyền dự định đi từ vị trí A bên bờ sông này đến vị trí B bên bờ sông kia...

    Tìm hệ số của x^15 trong khai triển (x^2 + 8)^12...

    Hai người đi xe từ A đến C. Người thứ nhất đi theo đường từ A đến B rồi từ B đến C...

    Hiện nay anh hơn em 13 tuổi biết sau 7 năm nữa tuổi anh gấp 2 lần tuổi em...

    Trung bình cộng số ngô ở hai thùng là 225 kg .Thùng B nhiều hơn thùng A là 120...

    Phân tích đa thức thành nhân tử: 81x^4 + 4y^4...

    Thực hiện phép tính: (6^2007 – 6^2006) : 6^2006...

    ​Có bao nhiêu cách xếp 3 quả bóng giống nhau vào 5 chỗ khác nhau...

    Hai người khách du lịch xuất phát đồng thời từ hai thành phố cách nhau 38 km...

    Gieo 3 con súc sắc cân đối và đồng chất. Xác suất để số chấm xuất hiện trên 3 con...

    Tại môt khu nghỉ dưỡng người ta muốn xây một cây cầu bắc qua ao sen (đoạn EF để...

    Một bể bơi có chiều dài 25m, chiều rộng 10m và sâu 1,5m...

    Có bao nhiêu số tự nhiên có chín chữ số mà các chữ số của nó viết theo thứ tự giảm...

    Trên cạnh BC của hình tam giác ABC có các điểm M,N sao cho BM = MN = NC...

    Có bao nhiêu cặp số nguyên (x; y) thỏa mãn 0 ≤ x ≤ 2020 và log2 (4x + 4) + x = y + 1...

    Có bao nhiêu số tròn nghìn có 5 chữ số...

    Bác Năm mới mua miếng đất hình vuông có diện tích 3600 m2. Bác tính làm hàng rào...

    Ta có thể trừ đi 1 từ số 1111 bao nhiêu lần...

    Một quả bóng được khâu từ 32 miếng da gồm hai loại như hình vẽ...

    Tìm x biết 12x + 9,28 . 12 = 240...

    Nêu cách vẽ tam giác cân...

    Khi đo chiều dài của chiếc bàn học, một học sinh viết được kết quả: C = 118 ± 2...

    Tại cửa hàng giá niêm yết một cái áo là 300000 đồng. Nếu bán với giá bằng ba phần...

    Một trường có 1030 học sinh. Số học sinh nam chiếm 40%. Tính số học sinh nữ...

    Có bao nhiêu số tự nhiên gồm 5 chữ số chia hết cho 10...

    Trong số 423,15 phần thập phân là...

    Cho nửa đường tròn tâm O đường kính AB =2R và điểm M nằm trên đường tròn đó...

    A = x(3x^2 – x + 5) – (2x^3 + 3x – 25) – x(x^2 – x + 2...

    Cho hàm số bậc nhất y = m – 1 + (m + 2)x. Tìm tọa độ điểm cố định mà đường thẳng...

    Tìm tập giá trị T của hàm số y = sin2x...

    Có 3 học sinh nữ và 2 học sinh nam. Ta muốn sắp xếp vào 1 bàn dài có 5 ghế ngồi...

    Làm tròn số 45,29 với độ chính xác d = 6...

    Số thập phân có 5 chữ số khác nhau lớn nhất mà số đó nhỏ hơn 100...

    Cho x + 2y = 5. Tính giá trị biểu thức A= x^2 + 4y^2 – 2x + 10 + 4xy – 4y...

    Xét mệnh đề kéo theo P: “Nếu 18 chia hết cho 3 thì tam giác cân có 2 cạnh bằng...

    3m 6cm = … dm...

    Cho tập hợp A={1;2;3;...;n} trong đó n là số nguyên dương lớn hơn 1...

    Có bao nhiêu tập hợp X thỏa mãn điều kiện {0; 1; a} hợp với X = {0; 1; a; b; c...

    Một mảnh đất hình chữ nhật có chu vi 180m, chiều dài hơn chiều rộng 22m...

    Một hình tam giác có diện tích là 8m2 và độ dài cạnh đáy là 32dm. Tìm chiều cao của...

    Một xí nghiệp đóng giày dự định hoàn thành kế hoạch trong 26 ngày...

    Tại cửa hàng bán hoa giá bán ban đầu của một bó hoa là 60 000 đồng...

    Phân tích đa thức thành nhân tử: x^4y – xy^4...

    Cho hàm số y = (m–1)x + m – 4 (m là tham số và m khác 1...

    Để sản xuất một tờ giấy A5 lần 5 lít nước. Một cuốn sổ A5 có 300 trang...

    Tìm ước chung lớn nhất của 1 và 2019...

    1,2 ha = … m2...

    Một bồn hoa có dạng hình vuông có độ dài cạnh là 2m . Để làm lối đi rộng hơn...

    Công thức nào sau đây cho ta quan hệ với tỉ lệ thuận? A. y = –3x...

    Tìm x thoả mãn: x : 12 ; x ⋮ 18 và x < 250...

    Bán kính của một bánh xe ô tô là 0,25m. Tính chu vi bánh xe đó. Nếu ô tô đó đi hết...

    Tham khảo các loạt bài Toán khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 429 16/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: