Cho tam giác ABC có 3 góc nhọn, trực tâm H. Đường thẳng vuông góc với AB kẻ từ

Vietjack.me giới thiệu bộ câu hỏi ôn tập Toán có đáp án được biên soạn bám sát chương trình học giúp bạn ôn luyện và bổ sung kiến thức môn Toán tốt hơn. Mời các bạn đón xem:

1 539 02/02/2024

Trang trước

Trang sau

Cho tam giác ABC có 3 góc nhọn, trực tâm H. Đường thẳng vuông góc với AB kẻ từ

Đề bài: Cho tam giác ABC có 3 góc nhọn, trực tâm H. Đường thẳng vuông góc với AB kẻ từ B cắt đường thẳng vuông góc với AC kẻ từ C tại D .

a) Chứng minh tứ giác BHCD là hình bình hành.

b) Gọi M là trung điểm BC, O là trung điểm AD. Chứng minh 2OM = AH.

Lời giải:

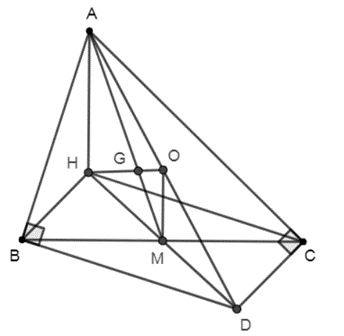
Tài liệu VietJack

a) Gọi AD và BE lần lượt là hai đường cao của ∆ABC .

Theo đề hai đường cao AD và BE cắt nhau tại H hay H là trực tâm của ∆ABC

⇒ CH là đường cao thứ 3 của ∆ABC

Do đó CH ⊥ AB (1)

mà BD ⊥ AB (gt) ⇒ CH // BD

Có BH ⊥ AC (BE là đường cao)

CD ⊥ AC

Do đó BH // CD (2)

Từ (1) và (2) suy ra : Tứ giác BHCD là hình bình hành

b) Có BHCD là hình bình hành nên 2 đường chéo cắt nhau tại trung điểm mỗi đường mà M là trung điểm của BC ⇒ M cũng là trung điểm của HD hay HM = DM

Có O là trung điểm của AD hay OA = OD

Xét ∆AHD có: HM = DM; OA = OD

Suy ra OM là đường trung bình của ∆AHD.

Do đó OM = $\frac{1}{2}$ AH hay AH = 2OM.

Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:

Cả ba con gà, vịt, ngỗng cân nặng 10,5 kg. Biết con gà cân nặng 1,5 kg...

Tính chiều cao ứng với cạnh 40 cm của một tam giác, biết góc kề với cạnh này ...

Tìm m để 2 đường thẳng (d) cắt nhau tại 1 điểm trên trục tung cho hàm số y ...

Cho hàm số bậc nhất y = (2m + 1)x + m – 2. Tìm m biết rằng góc tạo bởi đường thẳng ...

Cho hàm số y = (2m – 1)x + 2. Tìm m để: a) Hàm số đã cho là hàm số bậc nhất ...

Người ta trồng mía trên một khu đất hình chữ nhật có chiều rộng 130m ...

Có một số tiền, nếu mua kẹo loại 5 000 đồng một gói thì được 15 gói kẹo ...

Một gia đình gồm bố, mẹ và hai con (4 người), bình quân thu nhập hằng tháng là ...

Một lớp có 60 học sinh, trong đó có 36 học sinh giỏi toán, 21 học sinh giỏi văn ...

Có tất cả 18 quả táo, cam và xoài. Số quả cam bằng ...

Tổng của hai số là 90. Số thứ nhất bằng ...

Tính giá trị của biểu thức P = 18a + 30b + 7a – 5b. Biết a + b = 100 ...

Cho a, b, c > 0 thỏa mãn a^2 + b^2 + c^2 = 3. Tìm GTNN ...

Tìm x, biết: x^5 = x^3 ...

Trước đây mua 5 m vải phải trả 60 000 đồng. Hiện nay giá bán mỗi mét vải đã ...

Trung bình mỗi con gà đẻ ăn hết 104 g thức ăn trong một ngày. Hỏi trại chân nuôi cần ...

Phân tích đa thức thành nhân tử: x^2 – y^2 + 12y – 36 ...

Cho tam giác ABC có 3 góc nhọn, trực tâm H. Đường thẳng vuông góc với AB kẻ từ ...

Một người có số tiền không quá 70 000 đồng gồm 15 tờ giấy bạc với hai loại ...

Lớp 5A có 43 học sinh. Trong bài thi học kỳ một cả lớp đều được điểm 9 ...

Cho các số 0; 1; 2; 3; 4; 5; 6; 7. Từ các chữ số trên lập được bao nhiêu số có 4 chữ số ...

Một mảnh đất hình chữ nhật có nửa chu vi là 194 m chiều dài gấp 3 lần chiều rộng ...

Một can nhựa chứa 100 lít dầu hỏa. Biết một lít dầu hỏa cân nặng 0,8 kg ...

Một mảnh vải 4 m có giá 192 000 đồng. Một người mua 1,25 m vải đó để may áo ...

Một hình chữ nhật có nửa chu vi là 61,5 m, chiều rộng bằng ...

Một mảnh vườn hình chữ nhật có chiều dài 20 m và chiều rộng 15 m ...

Người thợ may lấy ra một tấm vải lớn để cắt may 25 bộ quần áo cho công ty ...

Một phân xưởng lắp ráp xe đạp, sáu tháng đầu năm phân xưởng đó lắp ráp được ...

Cho hai điểm A(–1; –2) và B(–4; 3). Lập phương trình đường thẳng (d) đi qua A, B ...

Cho đường tròn (O) và dây AB không đi qua tâm, gọi M là trung điểm AB ...

Khai triển biểu thức lượng giác cos4x theo cosx ...

Viết số thích hợp vào chỗ chấm: a) 178 dm = … m … dm ...

Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HM vuông góc với AB ...

Cho tam giác ABC và điểm S không thuộc mặt phẳng (ABC ...

Có 45 m vải may được 9 bộ quần áo như nhau. Hỏi phải dùng bao nhiêu m ...

Dấu hiệu chia hết cho 11 là gì? Có dấu hiệu chia hết cho 12 hay không ...

A = x^5 – 100x^4 + 100x^3 – 100x^2 + 100x – 9 tại x = 99 ...

Hỏi có bao nhiêu phân số thập phân khác 0 mà tổng của mẫu số và tử số là số lẻ ...

Tính (tính hợp lí nếu có thể): –3752 – (29 – 3632) – 51 ...

Tìm x, biết: (x + 1) + (x + 2) + (x + 3) + … + (x + 100) = 5050Tìm x, biết: (x + 1) + (x + 2) + (x + 3) + … + (x + 100) = 5050 ...

Tìm x, biết: (x + 1) + (x + 2) + (x + 3) + … + (x + 100) = 6050 ...

Giải phương trình: (x + 1)^3 – (x – 1)(x^2 + x + 1) – 2 = 0 ...

Phân tích đa thức thành nhân tử: x^5 – x^4 + x^3 – x^2 ...

Phân tích đa thức thành nhân tử: x^5 – x^4 – x^3 – x^2 – x – 2 ...

Tổng của hai số là 0,6. Thương của hai số cũng bằng 0,6. Tìm hai số đó ...

Tìm y biết: y × 1 + y × 1,5 + y × 2 + y × 2,5 + y × 3 + … + y × 5 = 94,5 ...

Cho đa giác đều gồm 2023 cạnh. Người ta sơn các đỉnh của đa giác bằng hai màu ...

Bác Tư trồng lúa mì trên hai mảnh đất, cuối năm thu được 5795 kg ...

Đường gấp khúc ABCD có AB bằng 15 cm, biết đường gấp khúc ABC dài hơn đường ...

Cho các số a, b, c. Biết a là số có một chữ số, b là số có hai chữ số, c là số có ...

1 539 02/02/2024

Trang trước

Trang sau

Xem thêm các chương trình khác: