Tính bán kính đường tròn ngoại tiếp hình thang cân biết hình thang cân ABCD

Vietjack.me giới thiệu bộ câu hỏi ôn tập Toán có đáp án được biên soạn bám sát chương trình học giúp bạn ôn luyện và bổ sung kiến thức môn Toán tốt hơn. Mời các bạn đón xem:

1 809 02/02/2024

Trang trước

Trang sau

Tính bán kính đường tròn ngoại tiếp hình thang cân biết hình thang cân ABCD

Đề bài: Tính bán kính đường tròn ngoại tiếp hình thang cân biết hình thang cân ABCD (AB song song CD) có AB = 6cm; CD = 8cm và đường cao AH = 7cm.

Lời giải:

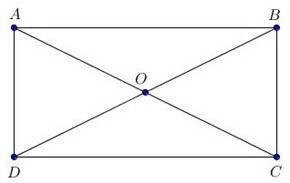
Tài liệu VietJack

Gọi M, N theo thứ tự là trung điểm của các cạnh đáy AB,CD của hình thang cân ABCD.

MN là trục đối xứng của hình tháng cân nên MN là đường trung trực của AB và CD.

Gọi O là giao điểm của MN với đường trung trực của BC.

O thuộc đường trung trực của AB nên OA = OB.

O thuộc đường trung trực của BC nên OB = OC.

O thuộc đường trung trực của CD nên OC = OD.

Vậy OA = OB = OC = OD, do đó đường tròn (O; OA) đi qua các điểm A, B, C, D.

Ta có AH = MN = 7cm (vì cùng là chiều cao của hình thang cân)

Theo định lý Pytago ta có:

OA² = OM² + MA²

OD² = ON² + DN²

Mà OA = OD

Nên: OM² + MA² = ON² + DN²

⇔ (MN – ON)² + 3² = ON² + 4²

⇔ (7 – ON)² = ON² + 7

⇔ 49 – 14ON + ON² = ON² + 7

⇔ ON = 3 (cm)

OD² = 3² + 4² = 25

Suy ra: OD = 5 (cm) vì OD > 0.

Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:

Có một tấm vải dài 35m. Người ta đem cắt thành các mảnh vải nhỏ, mỗi mảnh vải...

Cho a + b = 5; ab = 2. Tính a^2 + b^2 ...

Bạn Thanh giải một đề thi toán trắc nghiệm với 30 câu hỏi, cứ mỗi câu đúng bạn ...

Cho cấp số nhân (un) có số hạng đầu u1 = 6 và công bội q = 2. Tìm số hạng thứ tư ...

Có 8 viên bi trong đó có 1 viên bi nặng hơn sắt. Hỏi số lần tối thiểu cần thực hiện ...

Một cửa hàng thời trang có hình thức khuyến mãi sau: giảm giá 10% cho tất cả ...

Một hình chữ nhật có diện tích 15m2. Nếu tăng chiều dài lên hai lần, chiều rộng ...

Quãng sông từ bến A đến bến B là 24 km. Một chiếc thuyền xuôi dòng từ A đến B ...

Phân tích đa thức thành nhân tử: x^2 – 5x + 5y – y^2 ...

Tính nhanh : –72. 17 + 72.31 – 36.2.28 ...

Tính nhanh: 11 + (– 13) + 15 + (– 17) + ...... + 59 + (– 61 ...

Rút gọn biểu thức: 2x(x – 4)^2 – (x + 5)(x – 2)(x + 2) + 2(x + 5)^2 – (x – 1)^2 ...

Tìm x biết: 42 . x = 15,12 ...

B mua một con bò giá 10 triệu, bán 12 triệu. Vì tiếc nên B mua lại giá 15 triệu ...

Mua 5kg đường phải trả 85000 đồng. Hỏi mua 3,5kg đường cùng loại phải trả ít hơn ...

Một người dự định sửa nền và lát gach 60cm x 60cm. Biết rằng kích thước nền ...

Tìm x biết: x.(2013 – x) = 2013.2011 + 2013 ...

Tính giá trị biểu thức: (–15 – 25) : (–5) + (–13).3 ...

Tính nhanh – (– 2012 + 789) + (– 211) + (– 1012 – 1789 ...

Hai đường thẳng không có điểm chung gọi là gì ...

Cho hàm số bậc hai có đồ thị như hình vẽ. Hỏi hàm số đồng biến và nghịch biến ...

Có 6 học sinh và 2 thầy giáo được xếp thành hàng ngang. Hỏi có bao nhiêu cách xếp ...

Có bao nhiêu số tự nhiên có 5 chữ số khác nhau và là số chẵn ...

Tìm số thứ tư trong dãy số có 5 số chẵn liên tiếp biết tổng của năm số là 2020 ...

Tổng hai số bằng 37,72. Nếu số thứ nhất gấp lên 6 lần và giữ nguyên số thứ hai ...

Viết biểu thức (x − 2y)(x^2 + 2xy + 4y^2) dưới dạng hiệu hai lập phương ...

Một trường trung học phổ thông có 4 học sinh giỏi khối 12, có 5 học sinh giỏi ...

Tam giác ABC có cạnh đáy bằng gấp 3 lần chiều cao. Biết cạnh đáy hơn chiều cao ...

Chứng minh nếu m, n là số lẻ thì m^2 + n^2 chẵn ...

Một trang trại nuôi ong mật mua 75 chiếc can loại 10 lít để đựng mật ong ...

So sánh 2^200.2^100 và 3^100.3^100 ...

Có 4 người làm xong một công việc trong 5 ngày. Hỏi muốn làm xong công việc ...

So sánh 4^100 và 2^202 ...

Giải phương trình: x^4 + 3x^2 – 4 = 0 ...

Cho (O, 15 cm) có nghĩa là gì ...

Tìm x biết: 3x + 17 = 29 ...

Tìm n biết: 9^5n – 8 = 81 ...

Cho tổng A = 15 + 25 + x với x ∈ ℕ. Tìm x để A chia hết cho 5 ...

1 trường học bán trú chuẩn bị gạo đủ cho 120 học sinh trong 40 ngày sau ...

Tìm cạnh của hình vuông nếu cạnh của hình vuông giảm đi 7 m thì diện tích giảm ...

Tính bán kính đường tròn ngoại tiếp hình thang cân biết hình thang cân ABCD ...

Tìm số tự nhiên n sao cho n^2 – 14n – 256 là một số chính phương ...

Khai triển (x + 1)^2020 có bao nhiêu số hạng ...

Tính giá trị biểu thức: A = (1 – 3m)(9m^2 + 3m + l) – (6 – 26m^3) tại m = 5 ...

So sánh 17 yến và 170kg ...

Tính B = (a – b)(a^4 + a^3b + a^2b^2 + ab^3 + b^4 ...

Số 0.5 và –0.5 có phải số nguyên không ...

Tìm các hệ số a,b,c sao cho đa thức 3x^4 + ax^2 + bx + c chia hết cho đa thức ...

Tính giá trị biểu thức: (–63) – (–17 ...

So sánh 302mm^2 và 3dm^2 2mm^2 ...

Cho A = 2 + 2^2 + 2^3 + ... + 2^20. Chứng minh rằng ...

Tính giá trị: 36.4 – 4(82 – 7.11)^2 : 4 – 2016^0 ...

Nghiệm kép là gì ...

Trong các phát biểu sau, phát biểu nào là mệnh đề toán học ...

Số các ước tự nhiên của 252 là bao nhiêu? Liệt kê các ước của 252 ...

Tháng 11 vừa qua, có ngày Black Friday phần lớn các trung tâm thương mại ...

Dưới đây là phép nhân sai, hãy tìm phép nhân đúng ...

Giả sử ta dùng thước và compa vẽ hình thoi ABCD, biết AB = 5cm và AC = 8cm ...

Một hồ bơi dạng hình hộp chữ nhật có kích thước trong lòng hồ là...

So sánh 0,0125 và 0,005 ...

Tìm cạnh của hình vuông nếu cạnh của hình vuông giảm đi 7 m thì diện tích giảm ...

Bạn An kinh doanh hai mặt hàng handmade là vòng tay và vòng đeo cổ ...

Để kích cầu tiêu dùng sau mùa dịch Covid –19 lần thứ 4, một cửa hàng giày ...

Bạn An viết một trang web để kết bạn. Trang web đã nhận được 3 lượt truy cập ...

1 809 02/02/2024

Trang trước

Trang sau

Xem thêm các chương trình khác: