Cho hình chóp tứ giác S.ABCD, M là một điểm trên cạnh SB. Gọi E, F là hai điểm lần lượt thuộc miền trong tam giác

Vietjack.me giới thiệu bộ câu hỏi ôn tập Toán có đáp án được biên soạn bám sát chương trình học giúp bạn ôn luyện và bổ sung kiến thức môn Toán tốt hơn. Mời các bạn đón xem:

1 56 lượt xem

15000 câu hỏi ôn tập Toán (Phần 105)

Đề bài. Cho hình chóp tứ giác S.ABCD, M là một điểm trên cạnh SB. Gọi E, F là hai điểm lần lượt thuộc miền trong tam giác ABD và tam giác BCD. Tìm giao tuyến của mặt phẳng (MEF) và mặt phẳng (SCD).

Lời giải:

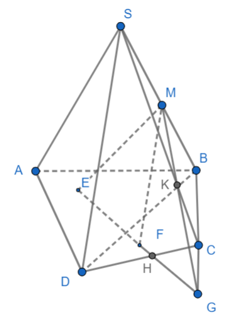Vì E,F lần lượt nằm ở miền trong của ABD, BCD nên EF ⊂ (ABCD)

Trong (ABCD) ta cho EF cắt CD, BC lần lượt tại H,G

Ta có H ∈ CD

⇒ H ∈ (MEF) ∩ (SCD)

Trong (SBC), ta có MG ⊂ (SCD), SC ⊂ (SCD) nên MG cắt SC tại K

⇒ K ∈ (SCD) ∩ (MEF) do K ∈ MG ⊂ (MEF)

Vậy (SCD) ∩ (MEF) = KH

Xem thêm các bài giải bộ 15000 câu hỏi Toán hay và chi tiết tại:

Cho x + y = 15. Tìm min, max $B = \sqrt{x - 4} + \sqrt{y - 3}$

Cho x,y,z là các số nguyên thỏa mãn: (x - y)(y - z)(z – x) = x + y + z. Chứng minh x + y + z chia hết cho 27.

Cho x, y, z thỏa mãn đk x + y + z = a. Tìm GTNN của $P = (1 + \frac{a}{x}) (1 + \frac{a}{y}) (1 + \frac{a}{z})$

Cho x + 3y – 4 = 0, tính x³ - x² + 9x²y - 9y² + 27xy² + 27y³ - 6xy

Chứng tỏ rằng (2²⁰²² + 2²⁰²¹ + 2²⁰²⁰) chia hết cho 7.

Tìm các hệ số a, b, c biết: (ax + b)(x² – cx + 2) = x³ + x² – 2 với mọi x

Chứng minh $\frac{1}{2 \sqrt{1}} + \frac{1}{3 \sqrt{2}} + \frac{1}{4 \sqrt{3}} + \dots + \frac{1}{2005 \sqrt{2004}} < 2$

Chứng minh $\frac{1}{65} < \frac{1}{5^{3}} + \frac{1}{6^{3}} + \dots + \frac{1}{2004^{3}} < \frac{1}{40}$

Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng: Tổng $\frac{1}{D I^{2}} + \frac{1}{D K^{2}}$ không đổi khi I thay đổi trên cạnh AB.

Chứng minh rằng F = 10²⁸ + 8 chia hết cho 72

Chứng minh $\frac{1 - 2 \sin^{2} x}{1 + \sin 2 x} = \frac{1 - \tan x}{1 + \tan x}$

Chứng minh tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường là hình bình hành.

Chứng minh n + 1 và 2n + 3 là hai số nguyên tố cùng nhau.

Chứng minh rằng nếu 5(m + n)² + mn ⋮ 441 thì mn ⋮ 441 (m, n ∈ ℤ)

Cho $\frac{a}{b} = \frac{c}{d}$ với a, b, c, d khác 0. Chứng minh $\frac{a}{a - b} = \frac{c}{c - d}$

Cho tứ giác ABCD. Chứng minh $\vec{A B} + \vec{C D} = \vec{A D} + \vec{C B}$

Cho tam giác ABC có BC = a, AC = b, Ab = c, đường phân giác AD.

1. Tính độ dài BD, DC.

2. Tia phân giác của góc B cắt AD tại I. Tính tỉ số AI : ID.

3. Cho BC bằng trung bình cộng của AB và AC, gọi G là trọng tâm của tam giác ABC. Chứng minh IG song song BC.

Chứng minh biểu thức $A = - x^{2} + \frac{2}{3} x - 1$ luôn âm với mọi giá trị của biến

Chứng minh với a, b dương thì $\sqrt{a + b} < \sqrt{a} + \sqrt{b}$

Có tồn tại hay không một dãy gồm 2019 số tự nhiên liên tiếp mà các số đó đều là hợp số?

Chứng minh đẳng thức sau: $\frac{(\sin x + \cos x)}{\sin^{3} x} = \cot^{3} x + \cot^{2} x \cot x + 1$

1 56 lượt xem

Xem thêm các chương trình khác: