Nội dung bài viết

    Xem thêm

    Công thức tính lực hướng tâm và cách giải các dạng bài tập (2024) chi tiết nhất

    Với tài liệu về Công thức tính lực hướng tâm và cách giải các dạng bài tập (2024) chi tiết nhất bao gồm: lý thuyết và bài tập cũng như những định nghĩa, tính chất, các dạng bài sẽ giúp bạn nắm vững kiến thức và học tốt môn Vật lí hơn.

    1 369 23/01/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Công thức tính lực hướng tâm và cách giải các dạng bài tập chi tiết nhất

    I. Lý thuyết

    1. Khái niệm

    - Lực hướng tâm là lực (hay hợp của các lực) tác dụng vào một vật chuyển động tròn đều và gây ra cho vật gia tốc hướng tâm.

    - Lực hướng tâm không phải là một loại lực mới, mà chỉ là một trong các lực đã học hay hợp lực của các lực đó. Nó gây ra gia tốc hướng tâm nên gọi là lực hướng tâm.

    Công thức tính lực hướng tâm

    2. Công thức

    Fht=maht=mv2r=mω2r (1)

    Trong đó:

    + m: khối lượng vật (kg)

    + v: tốc độ dài (m/s);

    + ω: tốc độ góc (rad/s);

    + R: bán kính quỹ đạo ( m)

    3. Kiến thức mở rộng

    - Từ công thức (1), ta tính được:

    + Gia tốc hướng tâm: aht=v2r=r.ω2

    + Khối lượng vật: m=Fhtaht

    + Bán kính quỹ đạo: r=v2aht=ahtω2=mv2Fht

    - Lực hấp dẫn giữa Trái Đất và vệ tinh nhân tạo đóng vai trò lực hướng tâm. Lực này gây ra cho vệ tinh gia tốc hướng tâm, giữ cho nó chuyển động tròn đều quanh Trái Đất.

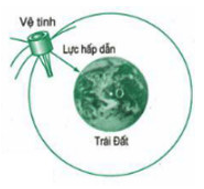
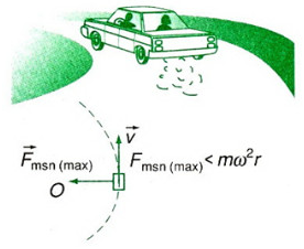
    Công thức tính lực hướng tâm

    - Chuyển động li tâm là chuyển động lệch ra khỏi quỹ đạo tròn theo phương tiếp tuyến với quỹ đạo của vật.

    + Trong chuyển động tròn của một vật, khi lực ma sát nghỉ cực đại không đủ lớn để đóng vai trò của lực hướng tâm, lúc này vật trượt trên mặt tiếp xúc rồi văng ra theo phương tiếp tuyến quỹ đạo.

    + Ứng dụng: máy vắt li tâm (trong máy giặt).

    + Tác hại: Khi tham gia giao thông trên những đoạn đường cong, khúc cua, nếu xe chạy với tốc độ lớn thì lực ma sát nghỉ cực đại không đủ lớn để đóng vai trò lực hướng tâm giữ cho xe chuyển động tròn nên xe sẽ trượt li tâm, dễ gây ra tai nạn giao thông. Vì vậy, để tránh gây tai nạn người ta thường lắp các biển báo xe đi chậm hay những đoạn đường cong phải được làm nghiêng về phía tâm cong.

    Công thức tính lực hướng tâm

    II. Bài tập vận dụng

    Câu 1: Một vệ tinh nhân tạo có khối lượng 100kg, được phóng lên quỹ đạo quanh Trái Đất ở độ cao 153km. Chu kì của vệ tinh chuyển động quanh Trái Đất là 5.103s và bán kính Trái Đất là R = 6400km. Tính độ lớn của lực hướng tâm tác dụng lên vệ tinh?

    Lời giải:

    Tốc độ góc: ω=2πT

    Lực hướng tâm: Fht=m.v2r=mω2r

    => Độ lớn lực hướng tâm tác dụng lên vệ tinh:

    Fht=mω2r=m4π2(R+h)T2=100.4π2.6553.1000(5.103)2≈1035 N

    Câu 2: Cho biết chu kì chuyển động của Mặt Trăng quanh Trái Đất là 27,32 ngày và khoảng cách từ Trái Đất đến Mặt Trăng là 3,84.108m. Hãy tính khối lượng của Trái Đất. Giả thiết quỹ đạo của Mặt Trăng là tròn.

    Lời giải:

    Khi Mặt Trăng chuyển động tròn quanh Trái Đất thì lực hấp dẫn giữa Mặt Trăng và Trái Đất đóng vai trò là lực hướng tâm, nên:

    Fhd=Fht⇔G.m.Mr2=m.v2r⇔GMr=v2

    Mà: v=ωr=2πTr

    ⇒GMr=4π2T2.r2⇒M=4π2r3T2G=4π2.(3,84.108)3(27,32.86400)2.6,67.10-11≈6.1024 kg

    Câu 3: Một vệ tinh nhân tạo bay quanh Trái Đất ở độ cao h bằng bán kính R của Trái Đất.Tính tốc độ dài của vệ tinh. Lấy g = 10 m/s2 ; R = 6 400 km.

    Lời giải:

    Ta có:

    Fht=Fhd⇒mg=mv2R⇒v=5660 m/s

    Câu 4: Bán kính Trái Đất là 6400 km. Tính tốc độ dài, chu kỳ quay, độ lớn lực hấp dẫn tác dụng lên vệ tinh khối lượng 600 kg chuyển động tròn đều quanh trái đất ở độ cao bằng bán kính trái đất, lấy g = 9,8 m/s2. Tính tốc độ dài, chu kì, độ lớn lực hấp dẫn tác dụng lên vệ tinh?

    Lời giải:

    r = 2.6400.103 m; m = 600kg, g = 9,8 m/s2

    Lực hấp dẫn đóng vai trò lực hướng tâm ⇒ Fhd = Fht

    Giải

    Fhd = Fht ⇒ GMmr2 = mv2r

    g = GMR2 ⇒ GM = gR2

    ⇒ v2 = GMr = gR2r ⇒ v = 5600 m/s

    T = 2π.rv = 14354s

    Fhd = Fht =mv2r= 1500 N

    Câu 5: Một vật có m = 500g chuyển động tròn đều trên đường tròn có r = 10 cm. Lực hướng tâm tác dụng lên vật 5 N. Tính tốc độ góc của vật.

    Lời giải:

    Ta có: Fht = mrω2 ⇒ ω = 10 rad/s

    Tham khảo các loạt bài Vật lí khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 369 23/01/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: