Nội dung bài viết

    Xem thêm

    Tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O, góc ABD = góc ACD

    Với giải Bài 54 trang 97 SBT Toán 8 Tập 2 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 8. Mời các bạn đón xem:

    1 32,626 25/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 8 Ôn tập chương 3 - Hình học

    Bài 54 trang 97 sách bài tập Toán 8 Tập 2: Tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O, ABD^=ACD^. Gọi E là giao điểm của hai đường thẳng AD và BC. Chứng minh rằng:

    a) ΔAOB đồng dạng ΔDOC;

    b) ΔAOD đồng dạng ΔBOC;

    c) EA.ED = EB.EC.

    * Lời giải:

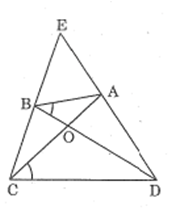
    Tài liệu VietJack

    a) Xét ΔAOB và ΔDOC, ta có:

    ABD^=ACD^ (giả thiết) Hay ABO^=OCD^

    AOB^=DOC^ (2 góc đối đỉnh)

    Vậy ΔAOB đồng dạng ΔDOC (g.g).

    b) Vì ΔAOB đồng dạng ΔDOC nên:

    AODO  =  OBOC  ⇒AOOB  =  DOOC

    Xét ΔAOD và BOC ta có:

    AOOB  =  DOOC (chứng minh trên).

    AOD^=BOC^ (đối đỉnh)

    Vậy ΔAOD đồng dạng ΔBOC (c.g.c)

    c) Vì ΔAOD đồng dạng ΔBOC nên: ADO^=BCO^ hay EDB^=ECA^

    Xét ΔEDB và ΔECA ta có:

    E^ chung

    EDB^=ECA^ (chứng minh trên)

    Vậy ΔEDB đồng dạng ΔECA (g.g)

    Suy ra: EDEC  = EBEA ⇒ ED.EA = EC.EB.

    * Phương pháp giải:

    - Áp dụng định nghĩa và tính chất của hai tam giác đồng dạng để chứng minh

    - Xem xét xem hai tam giác ở trường hợp đồng dạng thứ mấy để chứng minh cho đúng

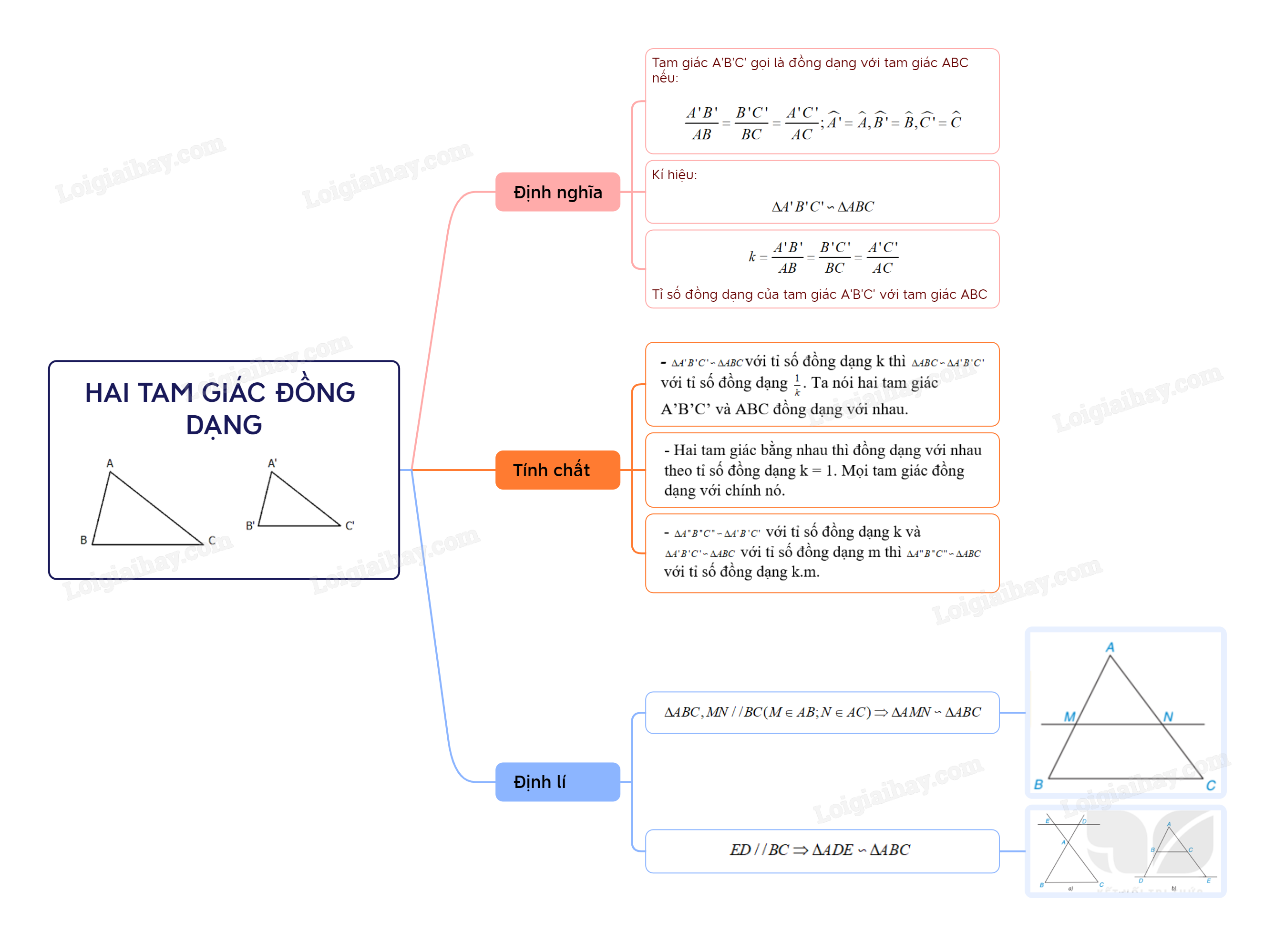
    *Lý thuyết

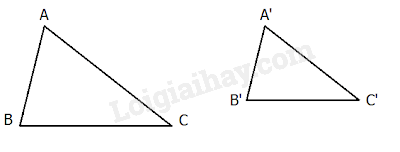
    1. Định nghĩa

    Tam giác A’B’C’ gọi là đồng dạng với tam giác ABC nếu:

    A′B′AB=B′C′BC=A′C′AC;A′^=A^,B′^=B^,C′^=C^

    Kí hiệu: ΔA′B′C′∽ΔABC (viết theo thứ tự cặp đỉnh tương ứng).

    Tỉ số k=A′B′AB=B′C′BC=A′C′AC là tỉ số đồng dạng của ΔA′B′C′ với ΔABC.

    Lý thuyết Hai tam giác đồng dạng (Kết nối tri thức 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 1)

    Nhận xét:

    - ΔA′B′C′∽ΔABCvới tỉ số đồng dạng k thì ΔABC∽ΔA′B′C′ với tỉ số đồng dạng 1k. Ta nói hai tam giác A’B’C’ và ABC đồng dạng với nhau.

    - Hai tam giác bằng nhau thì đồng dạng với nhau theo tỉ số đồng dạng k = 1. Mọi tam giác đồng dạng với chính nó.

    - ΔA″B″C″∽ΔA′B′C′ với tỉ số đồng dạng k và ΔA′B′C′∽ΔABC với tỉ số đồng dạng m thì ΔA″B″C″∽ΔABC với tỉ số đồng dạng k.m.

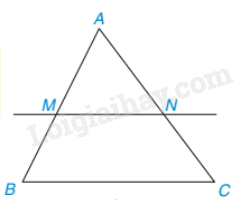
    2. Định lí

    Nếu một đường thẳng cắt hai cạnh của một tam giác là song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.

    Lý thuyết Hai tam giác đồng dạng (Kết nối tri thức 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 2)

    ΔABC,MN//BC(M∈AB;N∈AC)⇒ΔAMN∽ΔABC

    Chú ý. Định lí trên vẫn đúng nếu thay bằng đường thẳng cắt phần kéo dài của hai cạnh tam giác.

    Lý thuyết Hai tam giác đồng dạng (Kết nối tri thức 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 3)

    ED//BC⇒ΔADE∽ΔABC

    Sơ đồ tư duy Hai tam giác đồng dạng

    Lý thuyết Hai tam giác đồng dạng – Toán lớp 8 Kết nối tri thức (ảnh 1)

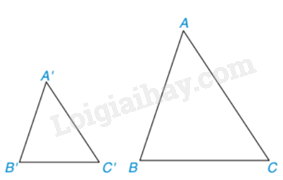
    a) Trường hợp đồng dạng thứ nhất của tam giác: cạnh - cạnh - cạnh :

    Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.

    {ΔABC,ΔA′B′C′;A′B′AB=B′C′BC=A′C′AC⇒ΔA′B′C′∽ΔABC

    Lý thuyết Ba trường hợp đồng dạng của hai tam giác (Kết nối tri thức 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 1)

    b) Trường hợp đồng dạng thứ nhất của tam giác: cạnh - góc - cạnh:

    Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng với nhau.

    {ΔABC,ΔA′B′C′;A′B′AB=A′C′AC,A′^=A^⇒ΔA′B′C′∽ΔABC

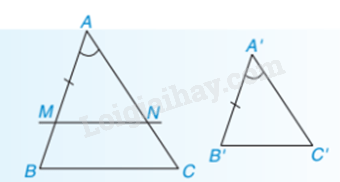
    Lý thuyết Ba trường hợp đồng dạng của hai tam giác (Kết nối tri thức 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 2)

    Nhận xét: Nếu ΔA′B′C′∽ΔABC theo tỉ số k và AM, A’M’ lần lượt là các đường trung tuyến của ΔABC và ΔA′B′C′ thì A′M′AM=k

    c) Trường hợp đồng dạng thứ nhất của tam giác: góc-góc:

    Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.

    {ΔABC,ΔA′B′C′;A′^=A^,B′^=B^⇒ΔA′B′C′∽ΔABC

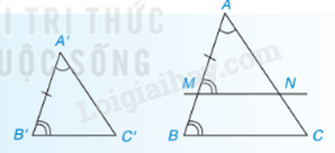
    Lý thuyết Ba trường hợp đồng dạng của hai tam giác (Kết nối tri thức 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 3)

    Nhận xét: ΔA′B′C′∽ΔABC theo tỉ số k và AM, A’M’ lần lượt là các đường phân giác của ΔABC và ΔA′B′C′ thì A′M′AM=k

    Xem thêm

    Lý thuyết Hai tam giác đồng dạng – Toán lớp 8 Kết nối tri thức

    TOP 40 câu Trắc nghiệm Khái niệm về hai tam giác đồng dạng (có đáp án ) - Toán 8

    Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:

    Bài 51 trang 97 SBT Toán 8 Tập 2: Cho tam giác ABC. a) Trên cạnh AB lấy điểm M sao cho...

    Bài 52 trang 97 SBT Toán 8 Tập 2: Tứ giác ABCD có hai góc vuông tại đỉnh A và C hai đường chéo AC và BD cắt nhau tại O...

    Bài 53 trang 97 SBT Toán 8 Tập 2: Cho hình chữ nhật ABCD có AB = a = 12cm, BC = b = 9m. Gọi H là chân đường vuông góc kẻ từ A xuống BD...

    Bài 55 trang 98 SBT Toán 8 Tập 2: Tam giác ABC có ba đường cao AD, BE, CF đồng quy tại H. Chứng minh rằng: AH.DH = BH.EH = CH.FH...

    Bài 56 trang 98 SBT Toán 8 Tập 2: Hai điểm M và K thứ tự nằm trên cạnh AB và BC của tam giác ABC; hai đoạn thẳng AK và CM cắt nhau tại P...

    Bài 57 trang 98 SBT Toán 8 Tập 2: Cho hình bình hành ABCD. Từ A kẻ AM vuông góc với BC, AN vuông góc CD (M thuộc BC và N thuộc CD)...

    Bài 58 trang 98 SBT Toán 8 Tập 2: Giả sử AC là đường chéo lớn của hình bình hành ABCD. Từ C, vẽ đường thẳng vuông góc CE...

    Bài 59 trang 98 SBT Toán 8 Tập 2: Tam giác ABC có hai đường cao là AD và BE (D thuộc BC và E thuộc AC). Chứng minh hai tam giác DEC và ABC là hai tam giác đồng dạng...

    Bài 60 trang 98 SBT Toán 8 Tập 2: Tam giác ABC có hai đường trung tuyến AK và CL cắt nhau tại O. Từ điểm P bất kì trên cạnh AC, vẽ các đường thẳng...

    Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

    Lý thuyết Ôn tập chương 3

    Trắc nghiệm Bài Ôn tập Chương 3 có đáp án

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 32,626 25/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: