Nội dung bài viết

    Xem thêm

    SBT Toán 8 Bài 1: Đa giác - Đa giác đều

    Với giải sách bài tập Toán lớp 8 Bài 1: Đa giác - Đa giác đều chi tiết được Giáo viên nhiều năm kinh nghiệm biên soạn bám sát nội dung sách bài tập Toán 8 Tập 1 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. 

    1 925 18/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Mục lục Giải SBT Toán 8 Bài 1: Đa giác - Đa giác đều

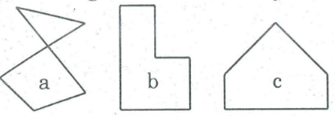
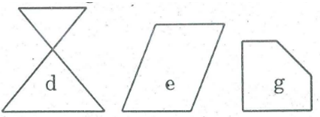
    Bài 1 trang 155 SBT Toán 8 Tập 1: Trong các hình dưới đây hình nào là đa giác lồi? Vì sao?

    Tài liệu VietJack

    Tài liệu VietJack

    Lời giải:

    Các hình c, e, g là các đa giác lồi vì đa giác nằm trên một nửa mặt phẳng với bờ chứa bất kỳ cạnh nào của đa giác.

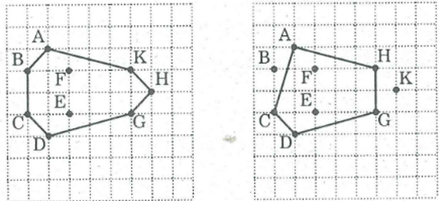
    Bài 2 trang 155 SBT Toán 8 Tập 1: Hình vẽ bên. Hãy vẽ một đa giác lồi mà các đỉnh là một trong các điểm đã cho trong hình.

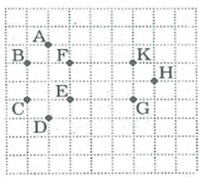
    Tài liệu VietJack

    Lời giải:

    Tài liệu VietJack

    Bài 3 trang 155 SBT Toán 8 Tập 1: Em hãy kể tên một số đa giác đều mà em biết.

    Lời giải:

    Ví dụ về các đa giác đều là: tam giác đều, hình vuông, ngũ giác đều, lục giác đều,…

    Bài 4 trang 156 SBT Toán 8 Tập 1: Chứng minh rằng số đo của một hình n-giác đều là (n−2).1800n .

    Lời giải:

    Vẽ một n-giác lồi, kẻ các đường chéo xuất phát từ một đỉnh của n-giác lồi thì chia đa giác đó thành (n - 2) tam giác.

    Tổng số đo 3 góc của 1 tam giác là 1800 nên tổng các góc của n-giác lồi bằng tổng các góc của (n - 2) tam giác bằng (n - 2).180o.

    Hình n-gíác đều có n góc bằng nhau nên số đo mỗi góc bằng: (n−2).1800n.

    Bài 5 trang 156 SBT Toán 8 Tập 1: Tính số đo của hình 8 cạnh đều, 10 cạnh đều, 12 cạnh đều.

    Lời giải:

    Theo bài  4, công thức tính số đo mỗi góc của đa giác đều có n cạnh: (n−2).1800n

    - Đa giác đều 8 cạnh ⇒ n = 8, số đo mỗi góc là:

    (​8−2).18008  =  1350

    - Đa giác đều 10 cạnh ⇒ n = 10, số đo mỗi góc là:

    (​10−2).180010  =  1440

    - Đa giác đều 12 cạnh ⇒ n = 12, số đo mỗi góc là:

    (​12−2).180012  =  1500

    Bài 6 trang 156 SBT Toán 8 Tập 1:

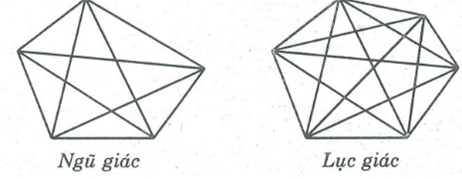
    a) Vẽ hình và tính số đường chéo của ngũ giác, lục giác.

    b) Chứng minh rằng hình n-giác có tất cả n(n−3)2 đường chéo.

    Lời giải:

    a) Từ mỗi đỉnh của ngũ giác vẽ được 2 đường chéo.

    Ngũ giác có 5 đỉnh ta kẻ được 5.2 = 10 đường chéo, trong đó mỗi đường chéo được tính hai lần. Vậy ngũ giác có tất cả 5 đường chéo.

    Từ mỗi đỉnh của lục giác vẽ được 3 đường chéo.

    Lục giác có 6 đỉnh ta kẻ được 6.3 = 18 đường chéo, trong đó mỗi đường chéo được tính hai lần. Vậy lục giác có tất cả 9 đường chéo.

    Tài liệu VietJack

    b) Từ mỗi đỉnh của n-giác nối với các đỉnh còn lại ta được n – 1 đoạn thẳng, trong đó có 2 đoạn thẳng là cạnh của hình n-giác (hai đoạn thẳng nối với hai đỉnh kề nhau).

    Vậy qua mỗi đỉnh n-giác vẽ được n – 3 đường chéo.

    Hình n-giác có n đỉnh kẻ được n(n – 3) đường chéo, trong đó mỗi đường chéo được tính hai lần.

    Vậy hình n-giác có tất cả n(n−3)2 đường chéo.

    Bài 7 trang 156 SBT Toán 8 Tập 1: Tìm số đường chéo của hình 8 cạnh, 10 cạnh, 12 cạnh.

    Lời giải:

    Áp dụng công thức tính ở bài 6 chương này.

    Đa giác có 8 cạnh, số đường chéo là: 8(8−3)2  =20 đường chéo;

    Đa giác có 10 cạnh, số đường chéo là: 10(10−3)2  =35 đường chéo;

    Đa giác có 12 cạnh, số đường chéo là: 12(12−3)2  =54 đường chéo.

    Bài 8 trang 156 SBT Toán 8 Tập 1: Chứng minh rằng tổng các góc ngoài của một đa giác (lồi) có số đo bằng 360o.

    Lời giải:

    Tổng số đo của góc trong và góc ngoài ở mỗi đỉnh của hình n-giác bằng 180o.

    Hình n-giác có n đỉnh nên tổng số đo các góc trong và góc ngoài của đa giác bằng n.180o.

    Mặt khác, ta biết tổng các góc trong của hình n-giác bằng (n – 2).180o.

    Vậy tổng số đo các góc ngoài của hình n-giác là:

    n.180o – (n – 2).180o 

    = n.180o – n.180o + 2.180o = 360o

    Bài 9 trang 156 SBT Toán 8 Tập 1: Đa giác nào có tổng số đo các góc trong bằng tổng số đo các góc ngoài?

    Lời giải:

    Hình n-giác lồi có tổng số đo các góc trong bằng (n – 2).180o và tổng các góc ngoài bằng 360o (theo bài 8).

    Để đa giác lồi có tổng các góc trong bằng tổng các góc ngoài thì:

    ⇒ (n – 2).180o = 360o 

    ⇒ n – 2 = 2 nên n = 4.

    Vậy tứ giác lồi có tổng các góc trong và góc ngoài bằng nhau.

    Bài 10 trang 156 SBT Toán 8 Tập 1: Một đa giác (lồi) có nhiều nhất là bao nhiêu góc nhọn?

    Lời giải:

    Ta có: nếu góc của đa giác lồi là góc nhọn thì góc ngoài tương ứng là góc tù.

    Nếu đa giác lồi có 4 góc đều nhọn thì các góc ngoài tương ứng đều là góc tù nên tổng các góc ngoài của đa giác lớn hơn 4.900 = 3600.

    Vậy đa giác lồi có nhiều nhất là 3 góc nhọn.

    Bài 11 trang 156 SBT Toán 8 Tập 1: Một đa giác đều có tổng số đo tất cả các góc ngoài và một góc trong của đa giác đó bằng 468°. Hỏi đa giác đều đó có mấy cạnh?

    Lời giải:

    Tổng số đo các góc ngoài của đa giác bằng 360°.

    Số đo một góc trong của đa giác đều là

    468° – 360° = 108°

    Gọi n là số cạnh của đa giác đều.

    Ta có số đo mỗi góc của đa giác đều bằng (n−2).1800n .

    Suy ra: (n−2).1800n = 108°

    ⇒ 180.n – 360 = 108.n

    ⇒ 72n = 360 ⇒ n = 5

    Vậy đa giác đều cần tìm có 5 cạnh.

    Bài tập bổ sung

    Bài 1.1 trang 156 SBT Toán 8 Tập 1: Mỗi câu sau đây đúng hay sai ?...

    Bài 1.2 trang 156 SBT Toán 8 Tập 1: a) Cho tam giác đều ABC. Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CA, AB. Chứng minh MNP là tam giác đều...

    Bài 1.3 trang 157 SBT Toán 8 Tập 1: Cho hình vuông ABCD có AB = 3cm Trên tia đối của tia BA lấy điểm K sao cho BK = 1cm...

    Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:

    Bài 2: Diện tích hình chữ nhật

    Bài 3: Diện tích tam giác

    Bài 4: Diện tích hình thang

    Bài 5: Diện tích hình thoi

    Bài 6: Diện tích đa giác

    Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

    Trắc nghiệm Đa giác. Đa giác đều có đáp án

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 925 18/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: