SBT Toán 8 Ôn tập chương 3 - Hình học

Mục lục Giải SBT Toán 8 Ôn tập chương 3 - Hình học

Bài 51 trang 97 SBT Toán 8 Tập 2: Cho tam giác ABC.

a) Trên cạnh AB lấy điểm M sao cho $\frac{AM}{MB}=\frac{2}{3}$;  tìm trên AC điểm N sao cho $\frac{AN}{NC}=\frac{2}{3}$.

b) Vẽ đoạn thẳng MN. Hỏi rằng hai đường thẳng MN và BC có song song với nhau không? Vì sao?

c) Cho biết chu vi và diện tích của tam giác ABC thứ tự là P và S.

Tính chu vi và diện tích tam giác AMN.

Lời giải:

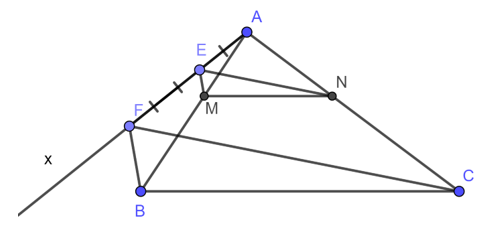
* Cách vẽ:

- Kẻ tia Ax bất kì khác tia AB, AC

- Trên tia Ax, lấy hai điểm E và F sao cho AE = 2 (đơn vị dài), EF = 3 (đơn vị dài)

- Kẻ đường thẳng FB

- Từ E kẻ đường thẳng song song với FB cắt AB tại M.

- Kẻ đường thẳng FC.

- Từ E kẻ đường thẳng song song với FC cắt AC tại N.

Ta có M, N là hai điểm cần vẽ.

* Chứng minh:

Trong ΔAFB, ta có: EM // FB.

Theo định lí Ta-lét, ta có: $\frac{AM}{MB}=\frac{AE}{E\text{}F}=\frac{2}{3}$

Trong ΔAFC, ta có: EN // FC.

Theo định lí ta-lét ta có: $\frac{AN}{NC}=\frac{AE}{E\text{}F}=\frac{2}{3}$.

Vậy M, N là hai điểm cần tìm.

b) Trong ΔABC, ta có: $\frac{AM}{MB}=\frac{AN}{NC}=\frac{2}{3}$

Suy ra: MN // BC (Theo định lí đảo của định lí Ta-lét)

c) Gọi p' và S' là chu vi và diện tích của ΔAMN.

Trong ΔABC, ta có: MN // BC

Suy ra: ΔAMN đồng dạng ΔABC

Và tỉ số đồng dạng $k=\frac{AM}{AB}=\frac{2}{5}$

$\Rightarrow \frac{P\text{'}}{P}=k=\frac{2}{5}\Rightarrow P\text{'}=\frac{2}{5}\text{}.\text{}P$

$\frac{S\text{'}}{S}=k^2={\left(\frac{2}{5}\right)}^2\Rightarrow S\text{'}=\frac{4}{25}\text{\hspace{0.17em}}S$

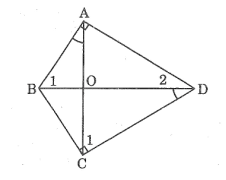
Bài 52 trang 97 SBT Toán 8 Tập 2: Tứ giác ABCD có hai góc vuông tại đỉnh A và C hai đường chéo AC và BD cắt nhau tại O, $\widehat{BAO}=\widehat{BDC}$. Chứng minh:

a) ΔABO đồng dạng ΔDCO;

b) ΔBCO đồng dạng ΔADO.

Lời giải:

a) Xét ΔABO và ΔDCO,ta có:

$\widehat{BAO}=\widehat{BDC}$ (giả thiết)

Hay $\widehat{BAO}=\widehat{ODC}$

$\widehat{AOB}=\widehat{DOC}$ (đối đỉnh)

Vậy ΔABO đồng dạng ΔDCO (g.g).

b) Vì ΔABO đồng dạng ΔDCO nên:

${\widehat{B}}_1={\widehat{C}}_1$ (1)

Mà ${\widehat{C}}_1+\widehat{BCA}=\widehat{BCD}=90°$  (2)

Trong ΔABD, ta có: $\hat{A}$ = 90^o

Suy ra: ${\widehat{B}}_1+{\widehat{D}}_2$ = 90^o (3)

Từ (1), (2) và (3): Suy ra: $\widehat{BCA}={\widehat{D}}_2$

Xét ΔBCO và ΔADO, ta có:

$\widehat{BCA}={\widehat{D}}_2$ (chứng minh trên)

$\widehat{AOD}=\widehat{BOC}$ (đối đỉnh)

Vậy ΔBOC đồng dạng ΔADO (g.g).

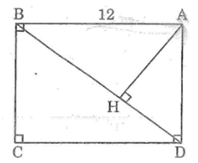
Bài 53 trang 97 SBT Toán 8 Tập 2: Cho hình chữ nhật ABCD có AB = a = 12cm, BC = b = 9m. Gọi H là chân đường vuông góc kẻ từ A xuống BD.

a) Chứng minh ΔAHB đồng dạng ΔBCD;

b) Tính độ dài đoạn thẳng AH;

c) Tính diện tích tam giác AHB.

Lời giải:

a)Xét ΔAHB và ΔBCD, ta có:

$\widehat{AHB}=\widehat{BCD}$ = 90^o

AB // CD (gt) nên $\widehat{ABH}=\widehat{BDC}$ (so le trong)

Vậy ΔAHB đồng dạng ΔBCD (g.g)

b) Vì ΔAHB đồng dạng ΔBCD nên: $\frac{AH}{BC}=\frac{AB}{BD}$

Suy ra: $AH=\frac{AB.BC}{BD}$ .

Áp dụng định lí Pi-ta-go vào tam giác vuông BCD, ta có:

BD² = BC² + CD² = BC² + AB²

= 12² + 9² = 225

Suy ra: BD = 15cm

Vậy $AH=\frac{12.9}{15}=7,2cm$.

c) Vì ΔAHB đồng dạng ΔBCD với tỉ số đồng dạng: $k=\frac{AH}{BC}=\frac{7,2}{9}=0,8$ .

Ta có: $\frac{S_{AHB}}{S_{BCD}}$ = k² = 0,8² = 0,64 ⇒ S_AHB = 0,64S_BCD

Mà S_BCD = $\frac{1}{2}$BC.CD = $\frac{1}{2}$.12.9 = 54(cm²)

Vậy S_AHB = 0,64.S_BCD 

= 0,64. 54 = 34,56 (cm²).

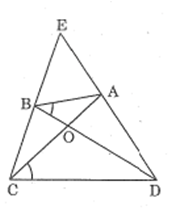
Bài 54 trang 97 SBT Toán 8 Tập 2: Tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O, $\widehat{ABD}=\widehat{ACD}$. Gọi E là giao điểm của hai đường thẳng AD và BC. Chứng minh rằng:

a) ΔAOB đồng dạng ΔDOC;

b) ΔAOD đồng dạng ΔBOC;

c) EA.ED = EB.EC.

Lời giải:

a) Xét ΔAOB và ΔDOC, ta có:

 $\widehat{ABD}=\widehat{ACD}$ (giả thiết)

Hay $\widehat{ABO}=\widehat{OCD}$

 $\widehat{AOB}=\widehat{DOC}$  (2 góc đối đỉnh)

Vậy ΔAOB đồng dạng ΔDOC (g.g).

b) Vì ΔAOB đồng dạng ΔDOC nên:

$\frac{AO}{DO}=\frac{OB}{OC}\Rightarrow \frac{AO}{OB}=\frac{DO}{OC}$

Xét ΔAOD và BOC ta có:

$\frac{AO}{OB}=\frac{DO}{OC}$ (chứng minh trên).

$\widehat{AOD}=\widehat{BOC}$   (đối đỉnh)

Vậy ΔAOD đồng dạng ΔBOC (c.g.c)

c) Vì ΔAOD đồng dạng ΔBOC nên: $\widehat{ADO}=\widehat{BCO}$ hay $\widehat{EDB}=\widehat{ECA}$

Xét ΔEDB và ΔECA ta có:

$\hat{E}$ chung

$\widehat{EDB}=\widehat{ECA}$ (chứng minh trên)

Vậy ΔEDB đồng dạng ΔECA (g.g)

Suy ra: $\frac{ED}{EC}=\frac{EB}{EA}$ ⇒ ED.EA = EC.EB.

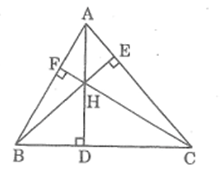
Bài 55 trang 98 SBT Toán 8 Tập 2: Tam giác ABC có ba đường cao AD, BE, CF đồng quy tại H. Chứng minh rằng: AH.DH = BH.EH = CH.FH.

Lời giải:

+)Xét ΔAFH và ΔCDH, ta có:

$\widehat{AFH}=\widehat{CDH}$ = 90^o

 $\widehat{AHF}=\widehat{CHD}$  ( 2 góc đối đỉnh)

Suy ra: ΔAFH đồng dạng ΔCDH (g.g)

Suy ra: $\frac{AH}{CH}=\frac{FH}{DH}$ .

Suy ra: AH.DH = CH.FH (1)

+) Xét ΔAEH và ΔBDH,ta có:

$\widehat{AEH}=\widehat{BDH}$ = 90^o

$\widehat{AHE}=\widehat{BHD}$ (2 góc đối đỉnh)

Suy ra: ΔAEH đồng dạng ΔBDH (g.g)

Suy ra: $\frac{AH}{BH}=\frac{EH}{DH}$

Suy ra: AH.DH = BH.EH (2)

Từ (1) và (2) suy ra: AH.DH = BH.EH = CH.FH ( điều phải chứng minh).

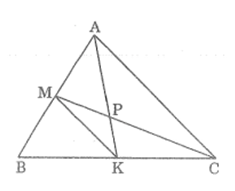
Bài 56 trang 98 SBT Toán 8 Tập 2: Hai điểm M và K thứ tự nằm trên cạnh AB và BC của tam giác ABC; hai đoạn thẳng AK và CM cắt nhau tại P. Biết AP = 2PK và CP = 2PM. Chứng minh rằng AK và CM là các trung tuyến của tam giác ABC.

Lời giải:

Xét ΔPAC và ΔPKM,ta có:

$\frac{PK}{PA}=\frac{1}{2};\frac{PM}{PC}=\frac{1}{2}$

Suy ra: $\frac{PK}{PA}=\frac{PM}{PC}$ .

Lại có: $\widehat{APC}=\widehat{KPM}$ (đối đỉnh)

Suy ra: ΔPKM đồng dạng ΔPAC(c.g.c) với tỉ số đồng dạng $k=\frac{1}{2}$.

Suy ra: $\frac{KM}{AC}=\frac{1}{2}$  (1)

Vì ΔPKM đồng dạng ΔPAC nên $\widehat{PKM}=\widehat{PAC}$

Suy ra: KM //AC (vì có cặp góc ở vị trí so le trong bằng nhau)

Trong ΔABC, ta có: KM // AC.

Suy ra: ΔBMK đồng dạng ΔBAC (g.g)

Suy ra: $\frac{BM}{BA}=\frac{BK}{BC}=\frac{MK}{AC}$   (2)

Từ (1) và (2) suy ra: $\frac{BM}{BA}=\frac{BK}{BC}=\frac{1}{2}$ 

Vì BM = $\frac{1}{2}$BA nên M là trung điểm AB.

Vì BK = $\frac{1}{2}$BC nên K là trung điểm BC.

Do đó CM, AK là các trung tuyến của tam giác ABC.

Bài 57 trang 98 SBT Toán 8 Tập 2: Cho hình bình hành ABCD. Từ A kẻ AM vuông góc với BC, AN vuông góc CD (M thuộc BC và N thuộc CD). Chứng minh rằng tam giác MAN đồng dạng với tam giác ABC.

Lời giải:

* Trường hợp góc B nhọn:

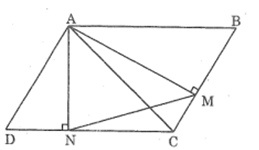
Xét ΔAMB và ΔAND, ta có:

$\widehat{AMB}=\widehat{AND}$ = 90^o

 $\widehat{B}=\widehat{D}$ (t/chất hình bình hành)

Suy ra ΔAMB đồng dạng ΔAND (g.g)

Suy ra: $\frac{AM}{AN}=\frac{AB}{AD}\Rightarrow \frac{AM}{AB}=\frac{AN}{A\text{}D}$  .

Mà AD = BC (tính chất hình hình hành)

Suy ra $\frac{AM}{AB}=\frac{AN}{BC}$.

Lại có: AB // CD (giả thiết) và AN ⊥ CD (giả thiết).

Suy ra: AN ⊥ AB hay $\widehat{NAB}$ = 90^o

Suy ra: $\widehat{NAM}+\widehat{MAB}$ = 90^o (1)

Trong tam giác vuông AMB ta có $\widehat{AMB}$ = 90^o

Suy ra: $\widehat{MAB}+\widehat{B}$ = 90^o (2)

Từ (1) và (2) suy ra: $\widehat{NAM}=\widehat{B}$

Xét ΔABC và ΔMAN ta có:

$\frac{AM}{AB}=\frac{AN}{BC}$ (chứng minh trên)

$\widehat{NAM}=\widehat{B}$ (chứng minh trên)

Vậy ΔABC đồng dạng ΔMAN (c.g.c).

* Trường hợp góc B tù:

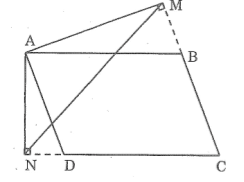
Xét ΔMAN và ΔAND, ta có:

$\widehat{AMB}=\widehat{AND}$ = 90^o

$\widehat{ABM}=\widehat{ADN}$ (vì cùng bằng $\hat{C}$)

Suy ra ΔAMB đồng dạng ΔAND (g.g)

Suy ra: $\frac{AM}{AN}=\frac{AB}{AD}\Rightarrow \frac{AM}{AB}=\frac{AN}{AD}$.

Mà AD = BC (tính chất hình bình hành)

Suy ra: $\frac{AM}{AB}=\frac{AN}{BC}$.

Vì AB // CD nên $\widehat{ABC}+\widehat{C}$ = 180^o (3)

Tứ giác AMCN có $\widehat{AMC}=\widehat{AND}$ = 90^o

Suy ra: $\widehat{MAN}+\widehat{C}$ = 180^o (4)

Từ (3) và (4) suy ra: $\widehat{MAN}=\widehat{ABC}$

Xét ΔAMN và ΔABC, ta có:

$\frac{AM}{AB}=\frac{AN}{BC}$ (chứng minh trên)

$\widehat{MAN}=\widehat{ABC}$ (chứng minh trên)

Vậy ΔMAN đồng dạng ΔABC (c.g.c).

Vậy ta luôn có: tam giác MAN đồng dạng với tam giác ABC.

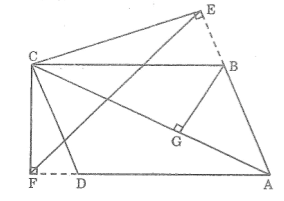
Bài 58 trang 98 SBT Toán 8 Tập 2: Giả sử AC là đường chéo lớn của hình bình hành ABCD. Từ C, vẽ đường thẳng vuông góc CE với đường thẳng AB, đường vuông góc CF với đường thẳng AD (E, F thuộc phần kéo dài của các cạnh AB và AD). Chứng minh rằng AB.AE + AD.AF = AC².

Lời giải:

Dựng BG ⊥ AC.

Xét ΔBGA và ΔCEA, ta có:

 $\widehat{BGA}=\widehat{CEA}$ = 90^o

$\hat{A}$ chung

Suy ra ΔBGA đồng dạng ΔCEA(g.g)

Suy ra: $\frac{AB}{AC}=\frac{AG}{AE}$ .

Suy ra: AB.AE = AC.AG (1)

Xét ΔBGC và ΔCFA, ta có:

$\widehat{BGC}=\widehat{CFA}$ = 90^o

 $\widehat{BCG}=\widehat{CAF}$  (so le trong vì AD // BC)

Suy ra ΔBGC đồng dạng ΔCFA (g.g)

Suy ra: $\frac{\text{}AF}{CG}=\frac{AC}{BC}$  ⇒ BC.AF = AC.CG

Mà BC = AD (tính chất hình bình hành)

Suy ra: AD.AF = AC.CG (2)

Cộng từng vế đẳng thức (1) và (2) ta có:

AB.AE + AD.AF = AC.AG + AC.CG

Hay AB.AE + AD.AF = AC(AG + CG)

Mà AG + CG = AC

nên AB.AE + AD.AF = AC².

(điều phải chứng minh).

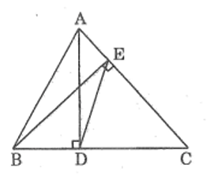
Bài 59 trang 98 SBT Toán 8 Tập 2: Tam giác ABC có hai đường cao là AD và BE (D thuộc BC và E thuộc AC). Chứng minh hai tam giác DEC và ABC là hai tam giác đồng dạng.

Lời giải:

Xét ΔADC và ΔBEC, ta có:

$\widehat{ADC}=\widehat{BEC}$ = 90^o

$\hat{C}$ chung

Suy ra: ΔADC đồng dạng ΔBEC (g.g)

Suy ra: $\frac{AC}{BC}=\frac{DC}{EC}\Rightarrow \frac{EC}{BC}=\frac{DC}{AC}$

Xét ΔDEC và ΔABC ta có:

$\frac{EC}{BC}=\frac{DC}{AC}$

$\hat{C}$ chung.

Vậy ΔDEC đồng dạng ΔABC (c.g.c)

Bài 60 trang 98 SBT Toán 8 Tập 2: Tam giác ABC có hai đường trung tuyến AK và CL cắt nhau tại O. Từ điểm P bất kì trên cạnh AC, vẽ các đường thẳng PE song song với AK, PF song song với CL (E thuộc BC, F thuộc AB). Các trung tuyến AK, CL cắt đoạn thẳng EF theo thứ tự tại M, N. Chứng minh rằng các đoạn thẳng FM, MN, NE bằng nhau.

Lời giải:

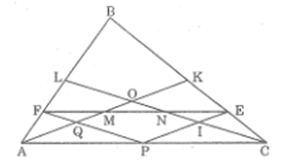
Gọi Q là giao điểm của PF và AK, I là giao điểm của PE và CL.

Trong ΔFPE ta có: PE // AK hay QM // PE

Suy ra: $\frac{F\text{}Q}{F\text{}P}=\frac{FM}{F\text{}E}$  (định lí ta-lét) (1)

Trong ΔALO ta có:PF // CL hay FQ // LO

Suy ra: $\frac{A\text{}F}{AL}=\frac{FQ}{L\text{}O}$ (định lí ta-lét) (2).

Trong ΔALC ta có: PF // CL

Suy ra:$\frac{A\text{}F}{AL}=\frac{FP}{CL}$   (định lí ta-lét) (3)

Từ (2) và (3) suy ra: $\frac{FQ}{LO}=\frac{FP}{CL}\Rightarrow \frac{FQ}{FP}=\frac{LO}{CL}$ .

Vì LO = $\frac{1}{3}$CL (O giao điểm của hai đường trung tuyến, nên O là trọng tâm tam giác BAC) nên $\frac{F\text{}Q}{FP}=\frac{1}{3}$  (4)

Từ (1) và (4) suy ra: $\frac{F\text{}M}{FE}=\frac{1}{3}\Rightarrow \text{}FM=\frac{1}{3}F\text{}E$ .

Trong ΔEPF ta có: PF // CL hay NI // PF

Suy ra: $\frac{EI}{EP}=\frac{EN}{E\text{}F}$ (định lí ta –lét) (5)

Trong ΔCKO ta có: EI // OK

Suy ra: $\frac{CE}{CK}=\frac{EI}{KO}$  (định lí ta –lét) (6)

Trong ΔCKA ta có: PE // AK

Suy ra: $\frac{CE}{CK}=\frac{EP}{AK}$  (định lí ta –lét) (7)

Từ (6) và (7) suy ra: $\frac{EI}{OK}=\frac{EP}{AK}\Rightarrow \frac{EI}{EP}=\frac{OK}{AK}$ .

Vì OK = $\frac{1}{3}$AK (O là trọng tâm tam giác ABC) nên $\frac{EI}{EP}=\frac{1}{3}$  (8)

Từ (5) và (8) suy ra: $\frac{EN}{EF}=\frac{1}{3}\Rightarrow EN=\frac{1}{3}EF$.

Ta có: MN = EF - (EN + FM) = $E\text{}F-\left(\frac{1}{3}\text{}EF\text{\hspace{0.17em}\hspace{0.17em}}+\frac{1}{3}\text{}EF\right)\text{\hspace{0.17em}\hspace{0.17em}}=\frac{1}{3}\text{}EF$

Vậy EN = MN = NF  (điều phải chứng minh).

Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:

Bài 1: Hình hộp chữ nhật

Bài 2: Hình hộp chữ nhật (tiếp)

Bài 3: Thể tích của hình hộp chữ nhật

Bài 4: Hình lăng trụ đứng

Bài 5: Diện tích xung quanh của hình lăng trụ đứng

Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

Lý thuyết Ôn tập chương 3

Trắc nghiệm Bài Ôn tập Chương 3 có đáp án