Nội dung bài viết

    Xem thêm

    SBT Toán 8 Bài 10: Đường thẳng song song với một đường thẳng cho trước

    Với giải sách bài tập Toán lớp 8 Bài 10: Đường thẳng song song với một đường thẳng cho trước chi tiết được Giáo viên nhiều năm kinh nghiệm biên soạn bám sát nội dung sách bài tập Toán 8 Tập 1 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. 

    1 983 18/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Bài 10: Đường thẳng song song với một đường thẳng cho trước

    Bài 124 trang 95 SBT Toán 8 Tập 1: Cho đoạn thẳng AB, kẻ tia Ax bất kỳ, lấy các điểm C, D, E sao cho AC = CD = DE. Qua C, D kẻ đường thẳng song song với BE. Chứng minh rằng đoạn thẳng AB bị chia ra ba phần bằng nhau.

    Lời giải:

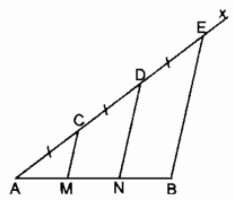
    Cho đoạn thẳng AB, kẻ tia Ax bất kỳ, lấy các điểm C, D, E sao cho AC = CD = DE (ảnh 1)

    Gọi giao điểm của các đường thẳng kẻ từ C và D song song với BE cắt AB tại M và N.

    Ta có: AC = CD = DE (giả thiết)

    CM // DN // BE

    Theo tính chất đường thẳng song song cách đều, ta có:

    AM = MN = NB.

    Vậy đoạn thẳng AB bị chia ra ba phần bằng nhau.

    Bài 125 trang 95 SBT Toán 8 Tập 1: Cho góc vuông xOy, điểm A nằm trên tia Oy, điểm B di chuyển trên tia Ox. Gọi C là điểm đối xứng với A qua B. Điểm C di chuyển trên đường nào?

    Lời giải:

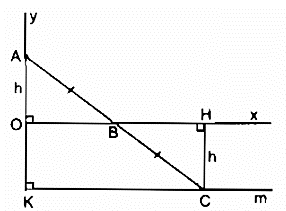
    Cho góc vuông xOy, điểm A nằm trên tia Oy, điểm B di chuyển trên tia Ox (ảnh 1)

    Vì điểm C đối xứng với điểm A qua điểm B nên BA = BC

    Kẻ CH ⊥ Ox

    Xét hai tam giác vuông AOB và CHB, ta có:

    AOB^=  CHB^ = 90o

    BA = BC (chứng minh trên)

    ABO^= CBH^ (đối đỉnh)

    Suy ra ΔAOB = Δ CHB ( cạnh huyền, góc nhọn)

    ⇒ CH = AO

    Vì A, O cố định nên OA không đổi suy ra CH không đổi

    Vì C thay đổi cách Ox một khoảng bằng OA không đổi nên C chuyển động trên đường thẳng song song với Ox, cách Ox một khoảng bằng OA.

    Khi B trùng O thì C trùng với điểm K đối xứng với A qua điểm O.

    Vậy C chuyển động trên tia Km // Ox, cách Ox một khoảng không đổi bằng OA.

    Bài 126 trang 96 SBT Toán 8 Tập 1: Cho tam giác ABC, điểm M di chuyển trên cạnh BC. Gọi I là trung điểm của AM. Điểm I di chuyển trên đường nào?

    Lời giải:

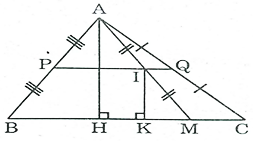
    Cho tam giác ABC, điểm M di chuyển trên cạnh BC (ảnh 1)

    Kẻ AH ⊥ BC, IK ⊥ BC ⇒ AH // IK

    Trong ΔAHM, ta có:

    AI = IM (do I là trung điểm của AM)

    IK // AH ( chứng minh trên)

    Suy ra IK là đường trung bình của ΔAHM

    ⇒ IK = 12AH

    Vì ΔABC cố định nên AH không thay đổi

    ⇒ IK = 12AH không đổi.

    Khi I thay đổi cách BC một khoảng bằng 12AH không đổi nên I nằm trên đường thẳng song song với BC, cách BC một khoảng bằng 12AH.

    Khi M trùng với điểm B thì I trùng với điểm P là trung điểm của AB.

    Khi M trùng với điểm C thì I trùng với điểm Q là trung điểm của AC.

    Vậy khi M di chuyển trên cạnh BC của ΔABC thì trung điểm I của AM chuyển động trên đường trung bình PQ của ΔABC.

    Bài 127 trang 96 SBT Toán 8 Tập 1: Cho tam giác ABC vuông tại A, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là chân đường vuông góc kẻ từ M đến AB, AC.

    a) So sánh độ dài AM, DE.

    b) Tìm vị trí của điểm M trên cạnh BC để DE có độ dài nhỏ nhất.

    Lời giải:

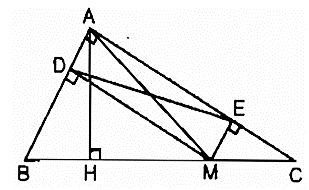
    Cho tam giác ABC vuông tại A, điểm M thuộc cạnh BC (ảnh 1)

    a) Xét tứ giác ADME, ta có:

    A^ = 90o (giả thiết)

    MD ⊥ AB (giả thiết)

    ⇒MDA^ = 90o

    Ta có: ME ⊥ AC (giả thiết)

    ⇒MEA^ = 90o

    Do đó, tứ giác ADME là hình chữ nhật (vì có ba góc vuông)

    ⇒ AM = DE (tính chất hình chữ nhật)

    b) Ta có: AH ⊥ BC nên AM ≥ AH (quan hệ đường vuông góc và đường xiên)

    Dấu “=” xảy ra khi M trùng với H

    Mà DE = AM ( chứng minh trên)

    Vậy DE có độ dài nhỏ nhất bằng AH khi M là chân đường vuông góc kẻ từ A đến BC.

    Bài 128 trang 96 SBT Toán 8 Tập 1: Cho điểm A nằm ngoài đường thẳng d. Điểm M di chuyển trên đường thẳng d. Gọi B là điểm đối xứng với A qua M. Điểm B di chuyển trên đường nào?

    Lời giải:

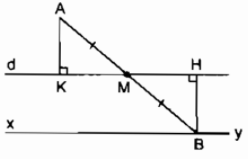
    Cho điểm A nằm ngoài đường thẳng d. Điểm M di chuyển trên đường thẳng d (ảnh 1)

    Kẻ AK ⊥ d, BH ⊥ d

    Vì M thay đổi trên d, B đối xứng với A qua M nên AM = MB.

    Xét tam giác vuông AKM và BHM.

    Ta có: AKM^  =  BHM^ = 90o

    AM = MB (chứng minh trên)

    AMK^= BMH^ (đối đỉnh)

    Do đó ΔAKM = ΔBHM (cạnh huyền - góc nhọn)

    ⇒ AK = BH

    Điểm A cố định, đường thẳng d cố định nên AK không đổi.

    Khi M thay đổi, B thay đổi cách đường thẳng d cố định một khoảng bằng AK không thay đổi nên B chuyển động trên đường thẳng xy song song với d và cách d một khoảng bằng AK.

    Bài 129 trang 96 SBT Toán 8 Tập 1: Cho đoạn thẳng AB, điểm M di chuyển trên đoạn thẳng ấy. Vẽ về một phía của AB các tam giác đều AMD, BME. Trung điểm I của DE di chuyển trên đường nào?

    Lời giải:

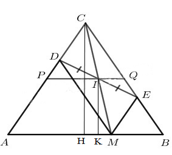
    Cho đoạn thẳng AB, điểm M di chuyển trên đoạn thẳng ấy (ảnh 1)

    Gọi C là giao điểm của AD và BE.

    Tam giác ABC có:

    A^= 60o (vì ΔADM đều)

    B^= 60o ( vì ΔBEM đều)

    Nên  C^ = 180o - A^ −  B^ = 60o

    Suy ra: ΔABC đều hay AB = AC = BC.

    Suy ra điểm C cố định.

    Lại có: A^=EMB^ = 60o

    Suy ra: ME // AC ( vì có cặp góc đồng vị bằng nhau) hay ME // CD.

    Do DMA^= BEM^ = 60o (hai tam giác AMD và BME là tam giác đều )

    Suy ra: MD // BC (vì có cặp góc so le trong bằng nhau ).

    Hay MD // EC

    Suy ra tứ giác CDME là hình bình hành.

    Ta có: I là trung điểm của DE nên I là trung điểm của CM

    Kẻ CH ⊥ AB, IK ⊥ AB

    ⇒IK // CH

    Trong ΔCHM,ta có:

    CI = IM và IK // CH

    Suy ra IK là đường trung bình của ΔCHM

    ⇒IK = 12CH

    Vì C cố định nên CH không đổi

    ⇒ IK = 12CH không đổi nên I chuyển động trên đường thẳng song song với AB, cách AB một khoảng bằng 12CH.

    Khi M trùng với A thì I trùng với trung điểm P của AC.

    Khi M trùng với B thì I trùng với trung điểm Q của BC.

    Vậy khi M chuyển động trên đoạn thẳng AB thì I chuyển động trên đoạn PQ ( P là trung điểm AC, Q là trung điểm BC).

    Bài 130 trang 96 SBT Toán 8 Tập 1: Hình chữ nhật ABCD có cạnh AD bằng nửa đường chéo AC. Tính góc nhọn tạo bới hai đường chéo.

    Lời giải:

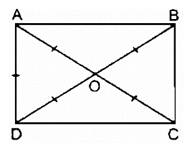
    Hình chữ nhật ABCD có cạnh AD bằng nửa đường chéo AC (ảnh 1)

    Gọi O là giao điểm của hai đường chéo AC và BD.

    Ta có: AC = BD (tính chất hình chữ nhật)

    ⇒ OA = OD = 12AC

    Lại có: AD = 12AC (giả thiết)

    Suy ra: OA = OD = AD

    ⇒ ΔOAD đều ⇒ AOD^ = 60o

    Bài 131 trang 96 SBT Toán 8 Tập 1: Dựng hình chữ nhật ABCD biết đường chéo AC = 4cm, góc tạo bởi hai đường chéo bằng 100o.

    Lời giải:

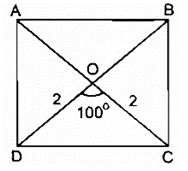
    Dựng hình chữ nhật ABCD biết đường chéo AC = 4cm (ảnh 1)

    * Cách dựng:

    - Dựng ΔOAB biết OA = OB = 2cm, AOB^ = 100o

    - Trên tia đối tia OA dựng điểm C sao cho OC = OA = 2cm

    - Trên tia đối tia OB dựng điểm D sao cho OD = OB = 2cm

    Nối AD, BC, CD ta có hình chữ nhật ABCD cần dựng.

    * Chứng minh:

    Ta có: OA = OC, OB = OD

    Suy ra tứ giác ABCD là hình bình hành.

    Vì AC = BD = 4 (cm) nên hình bình hành ABCD là hình chữ nhật.

    Bài tập bổ sung

    Bài 10.1 trang 96 SBT Toán 8 Tập 1: Tập hợp giao điểm hai đường chéo của hình chữ nhật ABCD có A và B cố định là...

    Bài 10.2 trang 96 SBT Toán 8 Tập 1: Cho góc xOy cố định khác góc bẹt. Các điểm A và B theo thứ tự chuyển động trên các tia Ox và Oy sao cho OA = OB...

    Bài 10.3 trang 96 SBT Toán 8 Tập 1: Xét các hình bình hành ABCD có cạnh AD cố định, cạnh AB = 2cm. Gọi I là giao điểm của AC và BD...

    Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:

    Bài 11: Hình thoi

    Bài 12: Hình vuông

    Ôn tập chương 1 - Phần Hình học

    Bài 1: Đa giác - Đa giác đều

    Bài 2: Diện tích hình chữ nhật

    Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

    Trắc nghiệm Đường thẳng song song với một đường thẳng cho trước có đáp án

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 983 18/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: