SBT Toán 8 Ôn tập chương 1 - Phần Hình học
Với giải sách bài tập Toán lớp 8 Bài: Ôn tập chương 1 - Phần Hình học chi tiết được Giáo viên nhiều năm kinh nghiệm biên soạn bám sát nội dung sách bài tập Toán 8 Tập 1 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8.
Mục lục Giải SBT Toán 8 Ôn tập chương 1 - Phần Hình học
Bài 157 trang 99 SBT Toán 8 Tập 1: Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Tìm điều kiện của tứ giác ABCD để EFGH là:
Lời giải:
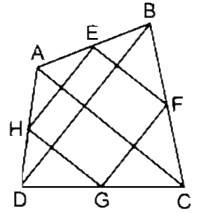
* Xét tam giác ABC có:
E là trung điểm của AB
F là trung điểm của BC
Do đó, EF là đường trung bình của ΔABC
Suy ra: EF //AC và EF = 12AC (1)
* Xét ΔADC có:
H là trung điểm của AD
G là trung điểm của DC
Do đó, HG là đường trung bình
Suy ra: HG // AC và HG = 12AC (2)
Từ (l) và (2) suy ra EF // HG và EF = HG.
Vậy tứ giác EFGH là hình bình hành.
Lại có: E là trung điểm của AB, H là trung điểm của AD nên EH là đường trung bình của tam giác ABD
EH // BD và EH = 12BD
a) Tứ giác EFGH là hình chữ nhật
⇔ EH ⊥ EF
Ta có: EF // AC nên để EH ⊥ EF thì EH ⊥ AC (quan hệ từ vuông góc đến song song)
Mà EH // BD nên AC ⊥ BD (quan hệ từ vuông góc đến song song)
Vậy để EFGH là hình chữ nhật thì tứ giác ABCD phải có AC ⊥ BD.
b) Tứ giác EFGH là hình thoi
⇔ EH = EF
Mà EH = 12BD; EF = 12AC (tính chất đường trung bình trong tam giác)
Do đó, để EFGH là hình thoi thì tứ giác ABCD phải có AC = BD
c) Tứ giác EFGH là hình vuông
⇔ tứ giác ABCD là hình thoi đồng thời là hình chữ nhật
Bài 158 trang 100 SBT Toán 8 Tập 1: Cho tam giác ABC vuông tại A, điểm D là trung điểm của BC. Gọi M là điểm đối xứng với D qua AB, E là giao điểm của DM và AB. Gọi N là điểm đối xứng với D qua AC, F là giao điểm của DN và AC.
a) Tứ giác AEDF là hình gì? Vì sao?
b) Các tứ giác ADBM, ADCN là hình gì? Vì sao?
c) Chứng minh rằng M đối xứng với N qua A.
d) Tam giác ABC có điều kiện gì thì tứ giác AEDF là hình vuông.
Lời giải:
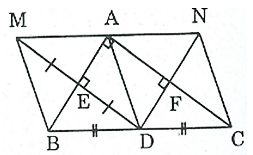
a) Điểm M và điểm D đối xứng qua trục AB
Suy ra AB là đường trung trực của đoạn thẳng MD
⇒ AB ⊥ DM ⇒ ^AED = 90o
Điểm D và điểm N đối xứng qua trục AC
⇒ AC là đường trung trực của đoạn thẳng DN
⇒ AC ⊥ DN ⇒ ^AFD = 90°
Xét tứ giác AEDF có
^EAF = 90o (giả thiết)
^AFD = 90°
^AED = 90o
Vậy tứ giác AEDF là hình chữ nhật (vì có 3 góc vuông).
b) Tứ giác AEDF là hình chữ nhật
⇒ DE // AC; DF // AB
Trong ∆ABC, ta có:
DB = DC (giả thiết)
Mà DE // AC
Suy ra: AE = EB (tính chất đường trung bình của tam giác)
Lại có: DF // AB và DB = DC
Suy ra: AF = FC (tính chất đường trung bình của tam giác)
Xét tứ giác ADBM, ta có:
AE = EB (chứng minh trên)
ED = EM (vì AB là trung trực DM)
Suy ra tứ giác ADBM là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)
Mặt khác: AB ⊥ DM
Vậy hình bình hành ADBM là hình thoi (vì có hai đường chéo vuông góc)
Xét tứ giác ADCN, ta có:
AF = FC (chứng minh trên)
DF = FN (vì AC là đường trung trực DN)
Suy ra tứ giác ADCN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường).
Lại có: AC ⊥ DN
Vậy hình bình hành ADCN là hình thoi (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
c) Tứ giác ADBM là hình thoi
⇒ AM // DB và AM = AD
Hay AM // BC và AM = AD (1)
Tứ giác ADCN là hình thoi
⇒ AN // DC và AD = AN
Hay AN // BC và AN = AD (2)
Từ (1) và (2) suy ra: AM trùng với AN hay M, A, N thẳng hàng.
Và AM = AN nên A là trung điểm của MN.
Vậy điểm M và điểm N đối xứng qua điểm A.
d) Hình chữ nhật AEDF trở thành hình vuông khi AE = AF
Ta có: AE = 12AB; AF = 12AC
Nên AE = AF ⇒ AB = AC.
Vậy nếu ∆ABC vuông cân tại A thì tứ giác AEDF là hình vuông.
a) Chứng minh rằng D đối xứng với E qua A.
b) Tam giác DHE là tam giác gì? Vì sao?
c) Tứ giác BDEC là hình gì? Vì sao?
d) Chứng minh rằng BC = BD + CE.
Lời giải:
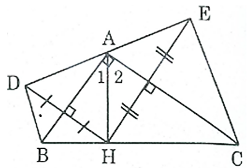
a) Điểm D đối xứng điểm H qua trục AB.
Suy ra AB là đường trung trực của HD
⇒ AH = AD (tính chất đường trung trực)
⇒ ΔADH cân tại A
Suy ra: AB là tia phân giác của ^DAH
⇒ ^DAB= ^A1
Điểm H và điểm E đối xứng qua trục AC
⇒ AC là đường trung trực của HE
⇒ AH = AE (tính chất đường trung trực)
⇒ ΔAHE cân tại A
Suy ra: AC là đường phân giác của góc ^HAE ⇒^A2= ^EAC
Ta có:
^DAH + ^HAE =^A1+^DAB+^A2+^CAE
=2(^A1+ ^A2)= 2.900=1800
⇒ D, A, E thẳng hàng.
Ta có: AD = AE (vì cùng bằng AH)
Suy ra điểm A là trung điểm của đoạn DE.
Vậy điểm D đối xứng với điểm E qua điểm A.
b) ΔADH cân tại A ⇒ ^AHD= ^ADH
ΔAEH cân tại A ⇒^AHE= ^AEH
⇒ ^DHE = ^AHD + ^AHE
= ^ADH+ ^AEH
Mà ^DHE + ^ADH+ ^AEH = 180o
⇒ ^DHE = 90o
Vậy ΔDHE vuông tại H.
c) Xét ΔADB và ΔAHB có:
^DAB= ^HAB ; AB chung; DA = AH
⇒ ΔADB = ΔAHB (c.g.c)
⇒ ^ADB = ^AHB = 90o ⇒ BD ⊥ DE
Chứng minh tương tự ^AEC= ^AHC = 90o
⇒ EC ⊥ DE
⇒ BD // EC và có ^BDE = 90°
⇒ BDEC là hình thang vuông.
d) Vì AB là đường trung trực của HD
⇒ BD = BH.
Vì AC là đường trung trực của HE
⇒ CE = CH.
Bài 160 trang 100 SBT Toán 8 Tập 1: Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, AC, CD, DB. Tìm điều kiện của tứ giác ABCD để EFGH là:
Lời giải:
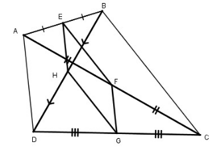
Xét tam giác ABC ta có:
E và F lần lượt là trung điểm của AB và AC
Nên EF là đường trung bình của tam giác ABC
Nên EF // BC, EF = 12BC (1)
Xét tam giác BDC có
H và G lần lượt là trung điểm của BD và CD
Nên HG là đường trung bình của tam giác BDC.
HG // BC, HG = 12BC (2)
Từ (1) và (2) ta có:
EF //HG, EF = HG.
Vậy EFGH là hình bình hành.
Tương tự, ta sẽ chứng minh được EH // FG, EH = FG.
a) EFGH là hình chữ nhật
⇔ EH ⊥ EF
Mà EH // AD nên EF ⊥ AD
Mặt khác EF // BC
⇔ AD ⊥ BC
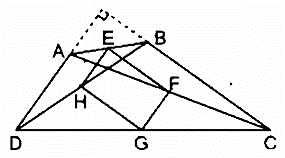
Vậy để EFGH là hình chữ nhật thì AD ⊥ BC.
b) EFGH là hình thoi ⇔ EH = EF
Mà EH = 12AD; EF = 12BC
⇔ AD = BC
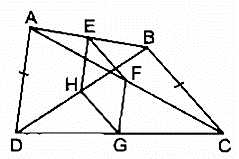
Vậy để EFGH là hình thoi thì AD = BC.
c) EFGH là hình vuông khi và chỉ khi EFGH là hình chữ nhật đồng thời là hình thoi
⇔ AD ⊥ BC và AD = BC
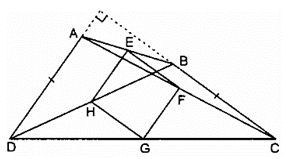
Vậy EFGH là hình vuông khi AD vuông góc với BC và AD = BC
Bài 161 trang 100 SBT Toán 8 Tập 1: Cho tam giác ABC, các đường trung tuyến BD, CE cắt nhau ở G. Gọi H là trung điểm của GB, K là trung điểm của GC.
a) Chứng minh rằng tứ giác DEHK là hình bình hành.
b) Tam giác ABC cần có điều kiện gì thì tứ giác DEHK là hình chữ nhật.
c) Nếu các đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình gì?
Lời giải:
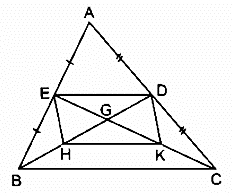
a) Tam giác ABC có hai đường trung tuyến BD và CE cắt nhau tại G nên G là trọng tâm tam giác ABC.
Ta có: GD = 12GB (tính chất đường trung tuyến của tam giác)
GH = 12GB (H là trung điểm của GB )
Suy ra: GD = GH.
Ta có: GE = 12GC (tính chất đường trung tuyến của tam giác)
GK = 12GC (K là trung điểm của GC)
Suy ra GE = GK.
Xét tứ giác DEHK có:
GE = GK
GD = GH
Do đó, tứ giác DEHK là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường).
b) Hình bình hành DEHK trở thành hình chữ nhật khi DH = EK
Mà DH = 23BD; EK = 23CE
Nên DH = EK ⇒ BD = CE
⇒ ΔABC cân tại A.
Vậy ΔABC cân tại A thì tứ giác DEHK là hình chữ nhật.
c) Nếu BD ⊥ CE ⇒ DH ⊥ EK.
Hình bình hành DEHK có hai đường chéo vuông góc nên nó là hình thoi.
Bài 162 trang 100 SBT Toán 8 Tập 1: Cho hình bình hành ABCD có AB = 2AD. Gọi E và F theo thứ tự là trung điểm của AB và CD.
a) Các tứ giác AEFD, AECF là hình gì? Vì sao?
c) Hình bình hành ABCD nói trên có thêm điều kiện gì thì EMFN là hình vuông.
Lời giải:
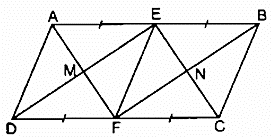
a) * Xét tứ giác AEFD, ta có:
AB // CD (vì ABCD là hình bình hành) hay AE // FD
AE = 12AB (vì E là trung điểm AB)
FD = 12CD (vì F là trung điểm của CD)
Suy ra: AE = FD.
Do đó, tứ giác AEFD là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
Lại có: AD = AE = 12AB .
Vậy tứ giác AEFD là hình thoi.
* Xét tứ giác AECF, ta có:
AE // CF (do ABCD là hình bình hành)
AE = 12AB (giả thiết)
CF = 12CD (giả thiết)
Suy ra: AE = CF.
Tứ giác AECF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
b) Tứ giác AEFD là hình thoi
⇒ AF ⊥ ED ⇒ ^EMF = 90o
AF // CE (vì tứ giác AECF là hình bình hành)
Mà AF ⊥ ED
Nên CE ⊥ ED ⇒ ^MEN = 90o
Xét tứ giác EBFD, ta có:
EB = FD (vì cùng bằng AE)
EB // FD (vì AB // CD)
Tứ giác EBFD là hình bình hành (vì có một cặp cạnh đổi song song và bằng nhau) ⇒ DE // BF
Mà DE ⊥ AF
Nên BF ⊥ AF ⇒ ^MFN = 90°
Xét tứ giác MENF có:
^MFN = 90°
^EMF = 90o
^MEN = 90o
Vậy tứ giác EMFN là hình chữ nhật.
c) Ta có: Hình chữ nhật EMFN là hình vuông ⇒ ME = MF
ME = 12DE (tính chất hình thoi)
MF = 12AF (tính chất hình thoi)
Suy ra: DE = AF.
⇒ Tứ giác AEFD là hình vuông (vì hình thoi có 2 đường chéo bằng nhau)
⇒ˆA = 90o ⇒ Hình bình hành ABCD là hình chữ nhật.
Ngược lại: ABCD là hình chữ nhật ⇒ˆA = 90o
Hình thoi AEFD có ˆA = 90o nên AEFD là hình vuông
⇒ AF = DE ⇒ ME = MF (tính chất hình vuông)
Hình chữ nhật EMFN là hình vuông (vì có 2 cạnh kề bằng nhau)
Vậy hình chữ nhật EMFN là hình vuông nếu ABCD là hình chữ nhật có AB = 2AD.
Bài 163 trang 100 SBT Toán 8 Tập 1: Cho hình bình hành ABCD có E, F theo thứ tự là trung điểm của AB, CD.
a) Tứ giác DEBF là hình gì? Vì sao?
b) Chứng minh rằng các đường thẳng AC, BD, EF cùng cắt nhau tại một điểm.
Lời giải:
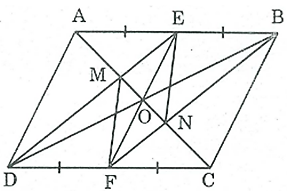
a) Xét tứ giác DEBF, ta có:
AB // CD (vì ABCD là hình bình hành) hay DF // EB
EB = 12AB (vì E là trung điểm AB)
DF = 12CD (vì F là trung điểm CD).
Suy ra: EB = DF.
Xét tứ giá DEBF có:
EB = DF
DF // EB
Tứ giác DEBF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
b) Gọi O là giao điểm của AC và BD.
Ta có: OB = OD (tính chất hình bình hành)
Tứ giác DEBF là hình bình hành nên EF và BD cắt nhau tại trung điểm của mỗi đường.
Suy ra: EF đi qua trung điểm O của BD.
Vậy AC, BD và EF cắt nhau tại O trung điểm của mỗi đoạn.
c) Xét ΔEOM và ΔFON có:
^MEO=^NFO (so le trong do DE // BF)
OE = OF (tính chất hình bình hành)
^MOE=^NOF (đối đỉnh )
Suy ra: ΔEOM = ΔFON (g.c.g)
⇒ OM = ON
Xét tứ giác EMFN ta có:
OM = ON
OE = OF
Do đó, tứ giác EMFN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường).
Bài 164 trang 101 SBT Toán 8 Tập 1: Cho đoạn thẳng AB = a. Gọi M là một điểm nằm giữa A và B. Vẽ về một phía của AB các hình vuông AMNP, BMLK có tâm theo thứ tự là C, D. Gọi I là trung điểm của CD.
a) Tính khoảng cách từ I đến AB.
b) Khi M di chuyển trên đoạn thẳng AB thì I di chuyển trên đường thằng nào?
Lời giải:
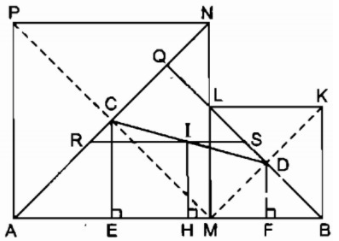
a) Kẻ CE ⊥ AB, IH ⊥ AB, DF ⊥ AB
Suy ra: CE // DF // IH
Mà IC = ID (giả thiết)
Nên IH là đường trung bình của hình thang DCEF
⇒ IH = DF + CE2
Vì C là tâm hình vuông AMNP nên ΔCAM vuông cân tại C.
CE ⊥ AM ⇒ CE là đường trung tuyến (tính chất tam giác cân)
⇒ CE = 12AM.
Vì D là tâm hình vuông BMLK nên ΔDBM vuông cân tại D.
DF ⊥ BM ⇒ DF là đường trung tuyến (tính chất tam giác cân)
⇒ DF = 12BM.
Vậy CE + DF = 12AM + 12BM
= 12(AM+BM)= 12AB= a2
Suy ra: IH = a22 = a4
b) Gọi Q là giao điểm của BL và AN.
Ta có: AN ⊥ MP (tính chất hình vuông)
BL ⊥ MK (tính chất hình vuông)
MP ⊥ MK (tính chất hình vuông)
Suy ra: BL ⊥ AN
⇒ ΔQAB vuông cân tại Q cố định.
Khi M thay đổi thì I thay đổi luôn cách đoạn thẳng AB cố định một khoảng không đổi bằng a4 nên I chuyển động trênđường thẳng song song với AB, cách AB một khoảng bằng a4.
Khi M trùng B thì I trùng với S là trung điểm của BQ.
Khi M trùng với A thì I trùng với R là trung điểm của AQ.
Vậy khi M chuyển động trên đoạn AB thì I chuyển động trên đoạn thẳng RS song song với AB, cách AB một khoảng bằng a4
Bài tập bổ sung
Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:
Bài 2: Diện tích hình chữ nhật
Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:
Xem thêm các chương trình khác:
- Tóm tắt tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 8 (hay nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Soạn văn 8 (ngắn nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Văn mẫu lớp 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Hóa học 8
- Giải sbt Hóa học 8
- Giải vở bài tập Hóa học 8
- Lý thuyết Hóa học 8
- Các dạng bài tập Hóa học lớp 8
- Giải sgk Vật Lí 8
- Giải sbt Vật Lí 8
- Lý thuyết Vật Lí 8
- Giải vở bài tập Vật lí 8
- Giải sgk Tiếng Anh 8 (sách mới) | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2
- Giải sgk Tiếng Anh 8 | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2 (sách mới)
- Giải sbt Tiếng Anh 8 (sách mới) | Sách bài tập Tiếng Anh 8
- Giải sbt Tiếng Anh 8 (thí điểm)
- Giải sgk Tin học 8 | Giải bài tập Tin học 8 Học kì 1, Học kì 2 (sách mới)
- Giải sgk Lịch Sử 8 | Giải bài tập Lịch sử 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Lịch sử 8 (sách mới) | Kiến thức trọng tâm Lịch sử 8
- Giải vở bài tập Lịch sử 8
- Giải Tập bản đồ Lịch sử 8
- Đề thi Lịch Sử 8
- Giải vở bài tập Sinh học 8
- Giải sgk Sinh học 8
- Lý thuyết Sinh học 8
- Giải sgk Giáo dục công dân 8 | Giải bài tập Giáo dục công dân 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Giáo dục công dân 8 (sách mới) | Kiến thức trọng tâm GDCD 8
- Lý thuyết Địa Lí 8 (sách mới) | Kiến thức trọng tâm Địa Lí 8
- Giải sgk Địa Lí 8 | Giải bài tập Địa Lí 8 Học kì 1, Học kì 2 (sách mới)
- Giải Tập bản đồ Địa Lí 8
- Đề thi Địa lí 8
