Nội dung bài viết

    Xem thêm

    SBT Toán 8 Bài 7: Trường hợp đồng dạng thứ ba (g.g)

    Với giải sách bài tập Toán lớp 8 Bài 7: Trường hợp đồng dạng thứ ba (g.g) chi tiết được Giáo viên nhiều năm kinh nghiệm biên soạn bám sát nội dung sách bài tập Toán 8 Tập 2 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. 

    1 1,177 19/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Mục lục Giải SBT Toán 8 Bài 7: Trường hợp đồng dạng thứ ba (g.g)

    Bài 39 trang 93 SBT Toán 8 Tập 2: Cho hình bình hành ABCD. Gọi E là trung điểm của AB, F là trung điểm của CD. Chứng minh hai tam giác ADE và CBF đồng dạng với nhau.

    Tài liệu VietJack

    Lời giải:

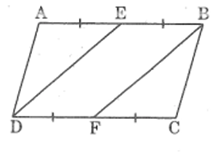
    Vì ABCD là hình bình hành nên:

    AB = CD (1)

    Theo giả thiết:

    AE = EB = 12AB (2)

    DF = FC = 12CD (3)

    Từ (1), (2) và (3) suy ra:

    EB = DF và BE // DF (do AB // CD).

    Suy ra tứ giác BEDF là hình bình hành (vì có cặp cạnh đối song song và bằng nhau)

    Suy ra: DE // BF

    Ta có: AED^=ABF^ (đồng vị)

     ABF^=BFC^  (so le trong)

    Suy ra: AED^=BFC^

    Xét ΔAED và ΔCFB ta có:

     AED^=BFC^ (chứng minh trên)

    A^=C^ (tính chất hình bình hành)

    Vậy: ΔAED đồng dạng ΔCFB (g.g).

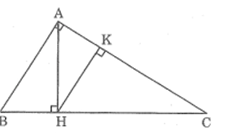
    Bài 40 trang 93 SBT Toán 8 Tập 2: Tam giác vuông ABC có A^ = 90° và đường cao AH. Từ H hạ HK vuông góc với AC.

    a) Trong hình đã cho có bao nhiêu tam giác đồng dạng với nhau?

    b) Hãy viết các cặp tam giác đồng dạng với nhau theo thứ tự các đỉnh tương ứng và viết tỉ lệ thức giữa các cặp cạnh tương ứng của chúng.

    Tài liệu VietJack

    Lời giải:

    a) Ta có:

    BAC^  =  AHC^  =  AHB^ = AKH^  =  HKC^  =900

    B^  = HAC^ = KHC^ (do HK // AB và cùng phụ góc BAH^) và C^  = AHK^ = BAH^.

    Trong hình trên có 5 tam giác đồng dạng với nhau theo từng đôi một  (theo trường hợp g- g) đó là:

    ΔABC; ΔHBA; ΔHAC; ΔKAH; ΔKHC.

    b) Các cặp tam giác đồng dạng với nhau theo thứ tự các đỉnh tương ứng và viết tỉ lệ thức giữa các cặp cạnh tương ứng của chúng:

    ΔABC đồng dạng ΔHBA.

    Ta có: ABHB  = BCBA =  ACHA

    ΔABC đồng dạng ΔHAC.

    Ta có: ABHA  = ACHC  = BCAC

    ΔABC đồngdạng ΔKHC.

    Ta có: ABKH  = ACKC  = BCHC

    ΔABC đồng dạng ΔKAH.

    Ta có: ABKA  =  ACKH  = BCAH

    ΔHBA đồng dạng ΔHAC.

    Ta có: HBHA  = HAHC  = BAAC

    ΔHBA đồng dạng ΔKHC.

    Ta có: HBKH  = HAKC  =  BAHC

    ΔHBA đồng dạng ΔKAH.

    Ta có: HBKA  = HAKH  = BAAH 

     ΔHAC đồng dạng ΔKHC.

    Ta có: HAKH  =  HCKC = ACHC

     ΔHAC đồng dạng ΔKAH.

    Ta có: HAKA  =  HCKH  = ACAH

    ΔKHC đồngdạng ΔKAH.

    Ta có:  KHKA  =  KCKH  =  HCAH.

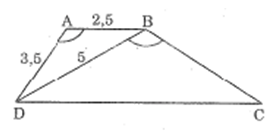
    Bài 41 trang 94 SBT Toán 8 Tập 2: Hình thang ABCD (AB // CD) có AB = 2,5cm, AD = 3,5cm, BD = 5cm và DAB^=DBC^.

    a) Chứng minh tam giác ADB đồng dạng với tam giác BCD.

    b) Tính độ dài BC, CD.

    c) Sau khi tính, hãy vẽ lại hình chính xác bằng thước và compa.

    Tài liệu VietJack

    Lời giải:

    a) Xét ΔABD và ΔBDC, ta có:

    DAB^=DBC^ (gt)

     ABD^=BDC^ (AB // CD, so le trong)

    Suy ra: ΔABD  ΔBDC (g.g)

    b)Vì ΔABD  ΔBDC nên: ABBD  =  ADBC  = BDDC   

    Với AB = 2,5cm; AD = 3,5cm; BD = 5cm,

    ta có:

     2,55  =  3,5BC  =  5DC⇒BC=  3,5.  52,5  =  7cm

    DC=  5. 52,5  =10cm.

    c) Vẽ hình thang ABCD

    - Bước 1: Vẽ tam giác ABD theo độ dài cho trước của mỗi cạnh

    - Bước 2: Lấy B làm tâm, quay cung tròn có bán kính 7cm, rồi lấy D làm tâm quay cung tròn có bán kính 10cm, hai cung này cắt nhau tại điểm C (khác phía với A so với BD).

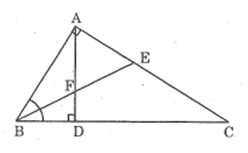
    Bài 42 trang 94 SBT Toán 8 Tập 2: Cho tam giác vuông ABC có A^ = 90o. Dựng AD vuông góc với BC (D thuộc BC). Đường phân giác BE cắt AD tại F.

    Chứng minh: FDFA  =  EAEC .

    Tài liệu VietJack

    Lời giải:

    Trong ΔABC, ta có BE là tia phân giác của góc ABC

    Suy ra: EAEC  =  ABBC (tính chất đường phân giác) (1)

    Trong ΔADB, ta có BF là tia phân giác của góc ABD

    Suy ra: FDFA  =  BDBA  (tính chất đường phân giác) (2)

    Xét ΔABC và ΔDBA, ta có:

    BAC^=BDA^=90°

    Góc B chung

    Suy ra: ΔABC đồng dạng ΔDBA (g.g)

    Suy ra: BDBA  =  ABBC  (3)

    Từ (1), (2) và (3) Suy ra: FDFA  =  EAEC .

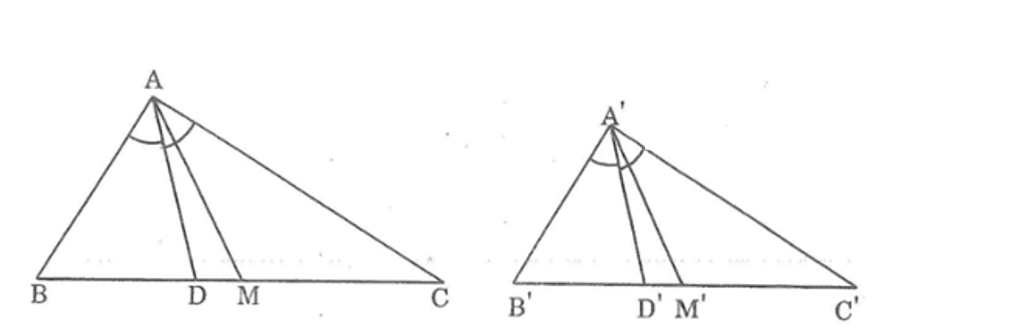
    Bài 43 trang 94 SBT Toán 8 Tập 2: Chứng minh rằng nếu hai tam giác ABC và A'B'C' đồng dạng với nhau thì:

    a) Tỉ số của hai đường phân giác tương ứng bằng tỉ số đồng dạng;

    b)Tỉ số của hai trung tuyến tương ứng bằng tỉ số đồng dạng.

    Tài liệu VietJack

    Lời giải:

    a) Vẽ đường phân giác AD, A’D’ theo thứ tự của hai tam giác ABC và A’B’C’

    Vẽ đường trung tuyến AM, A’M’ theo thứ tự của hai tam giác ABC và A’B’C’

    Vì ΔABC đồng dạng ΔA'B'C' nên ta có:

    A^=A'^;  B^=B'^ và A'B'AB =  k

    Lại có:

    BAD^  =  12  A^  (​gt);  B'A'D'^  = 12A'^​  (gt).

    Suy ra: BAD^=B'A'D'^

    Xét ΔABD và ΔA'B'D' ta có;

     B^=B'^ (chứng minh trên)

     BAD^=B'A'D'^ (chứng minh trên)

    Suy ra: ΔABD đồng dạng ΔA'B'D' (g.g)

    Vậy : A'D'AD =  A'B'AB  =  k.

    b) Vì ΔABC đồng dạng ΔA'B'C' nên B'C'BC  = k

    Mà B'M' = 12B'C' và BM = 12BC nên B'M'BM  =  k .

    Xét ΔABM và ΔA'B'M', ta có:

    A'B'AB  = B'M'BM  =  k

     B^=B'^  (chứng minh trên)

    Suy ra: ΔABM đồng dạng ΔA'B'M' (c.g.c).

    Vậy: AM'AM  =  A'B'AB  =  k .

    Bài tập bổ sung

    Bài 7.1 trang 94 SBT Toán 8 Tập 2: Hình bs.5 cho biết tam giác ABC có hai đường cao AD và BE cắt nhau tại H...

    Bài 7.2 trang 94 SBT Toán 8 Tập 2: Hình thang vuông ABCD (AB // CD) có đường chéo BD vuông góc với cạnh BC tại B...

    Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:

    Bài 8: Các trường hợp đồng dạng của tam giác vuông

    Ôn tập chương 3 - Hình học

    Bài 1: Hình hộp chữ nhật

    Bài 2: Hình hộp chữ nhật (tiếp)

    Bài 3: Thể tích của hình hộp chữ nhật

    Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

    Lý thuyết Trường hợp đồng dạng thứ ba

    Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,177 19/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: