Nội dung bài viết

    Xem thêm

    SBT Toán 8 Bài 4: Khái niệm hai tam giác đồng dạng

    Với giải sách bài tập Toán lớp 8 Bài 4: Khái niệm hai tam giác đồng dạng chi tiết được Giáo viên nhiều năm kinh nghiệm biên soạn bám sát nội dung sách bài tập Toán 8 Tập 2 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. 

    1 1,580 19/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Mục lục Giải SBT Toán 8 Bài 4: Khái niệm hai tam giác đồng dạng

    Bài 25 trang 89 SBT Toán 8 Tập 2: Cho hai tam giác A'B'C' và ABC đồng dạng với nhau theo tỉ số k. Chứng minh rằng tỉ số hai chu vi tam giác cũng bằng k.

    Lời giải:

    Vì ΔA'B'C' đồng dạng ΔABC theo tỉ số k nên ta có:

    A'B'AB  = B'C'BC  =  A'C'AC =  k

    Theo tính chất dãy tỉ số bằng nhau, ta có:

    A'B'AB  = B'C'BC  =  A'C'AC = A'B'+​ B'C'+​  C'A'AB+​BC ​+ ​CA

    Suy ra: A'B'+​ B'C'+​  C'A'AB+​BC ​+ ​CA  =  k

    Vậy chu​​  vi  ΔA'B'C'chu  vi  ΔABC  =  k  (điều phải chứng minh).

    Bài 26 trang 89 SBT Toán 8 Tập 2: Tam giác ABC có AB = 3cm, BC = 5cm, CA= 7cm. Tam giác A'B'C' đồng dạng với tam giác ABC có cạnh nhỏ nhất là 4,5cm. Tính các cạnh còn lại của tam giác A'B'C'.

    Lời giải:

    Tam giác A'B'C' đồng dạng với tam giác ABC có cạnh nhỏ nhất bằng 4,5 nên cạnh nhỏ nhất của Δ A'B'C' tương ứng với cạnh AB nhỏ nhất của ΔABC

    Giả sử A'B' là cạnh nhỏ nhất 'của Δ A'B'C'

    Vì Δ A'B'C' đồng dạng ΔABC nên A'B'AB  = A'C'AC  =  B'C'BC    (1)

    Thay AB = 3(cm), AC = 7(cm), BC = 5(cm), A'B' = 4,5(cm) vào (1) ta có: 

    4,53  =  A'C'7  =  ​B'C'5

    Vậy: A'C'=  7. 4,53  =10,5cm

    B'C'= 5. 4,53   =  7,5 ​​ cm

    Bài 27 trang 90 SBT Toán 8 Tập 2: Cho tam giác ABC có AB = 16,2cm, BC = 24,3cm, AC = 32,7cm. Tính độ dài các cạnh của tam giác A'B'C', biết rằng tam giác A'B'C đồng dạng với tam giác ABC và:

    a) A'B' lớn hơn cạnh AB là 10,8cm.

    b) A'B' bé hơn cạnh AB là 5,4cm.

    Lời giải:

    a) Vì ΔA'B'C' đồng dạng ΔABC nên A'B'AB  = A'C'AC  =  B'C'BC 

    Mà AB = 16,2 cm; BC = 24,3 cm; AC = 32,7 cm và A'B' lớn hơn cạnh AB là 10,8cm nên:

    A'B' = AB + 10,8 = 16,2 + 10,8 = 27 (cm)

    Ta có: 2716,2  =  A'C'32,7  = B'C'24,3

    Suy ra: A'C'=  32,7. 2716,2  = 54,5 (cm)

    Suy ra: B'C'= 24,3. 2716,2  =  40,5cm

    b) Vì Δ A'B'C' đồng dạng ΔABC nên A'B'AB  = A'C'AC  =  B'C'BC

    Mà AB = 16,2 cm; BC = 24,3 cm; AC = 32,7 cm và A'B' bé hơn cạnh AB là 5,4cm nên:

    A'B' = AB - 5,4 = 16,2 - 5,4 =10,8 (cm)

    Ta có: 10,816,2  =  A'C'32,7  = B'C'24,3

    Suy ra: A'C' = (10,8 . 32,7): 16,2 = 21,8 (cm)

    B'C' = (10,8 . 24,3): 16,2 = 16,2 (cm).

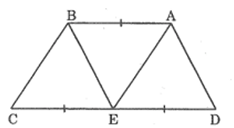
    Bài 28 trang 90 SBT Toán 8 Tập 2: Hình thang ABCD (AB // CD) có CD = 2AB. Gọi E là trung điểm của CD. Chứng minh rằng ba tam giác ADE, ABE và BEC đồng dạng với nhau từng đôi một (chú ý viết các đỉnh của hai tam giác đồng dạng theo thứ tự tương ứng với nhau).

    Tài liệu VietJack

    Lời giải:

    Vì CD = 2AB (gt) nên AB = 12CD

    Vì E là trung điểm của CD

    nên DE = EC = 12CD

    Suy ra: AB = DE = EC.

    Hình thang ABCD có đáy AB = EC nên hai cạnh bên AE và BC song song với nhau

    Xét ΔAEB và ΔCBE, ta có:

    ABE^=BEC^ (so le trong)

    AEB^=EBC^ (so le trong)

    BE cạnh chung

    Suy ra: ΔAEB = ΔCBE (g.c.g) (1)

    Hình thang ABCE có đáy AB = DE nên hai cạnh bên AD và BE song song với nhau

    Xét ΔAEB và ΔEAD, ta có:

    BAE^=AED^ (so le trong)

    AEB^=EAD^ (so le trong)

    AE cạnh chung

    Suy ra: ΔAEB = ΔEAD (g.c.g) (2)

    Từ (1) và (2) suy ra: ΔAEB = ΔCBE = ΔEAD

    Vậy ba tam giác ΔAEB; ΔCBE và ΔEAD đôi một đồng dạng.

    Bài tập bổ sung

    Bài 4.1 trang 90 SBT Toán 8 Tập 2: Tam giác ABC có tổng độ dài hai cạnh AB + AC = 10,75 cm và đồng dạng với tam giác...

    Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:

    Bài 5: Trường hợp đồng dạng thứ nhất (c.c.c)

    Bài 6: Trường hợp đồng dạng thứ hai (c.g.c)

    Bài 7: Trường hợp đồng dạng thứ ba (g.g)

    Bài 8: Các trường hợp đồng dạng của tam giác vuông

    Ôn tập chương 3 - Hình học

    Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

    Lý thuyết Khái niệm tam giác đồng dạng

    Trắc nghiệm Khái niệm về hai tam giác đồng dạng có đáp án

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,580 19/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: