SBT Toán 8 Bài 8: Đối xứng tâm

Mục lục Giải SBT Toán 8 Bài 8: Đối xứng tâm

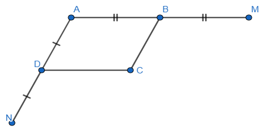
Bài 92 trang 91 SBT Toán 8 Tập 1: Cho hình 13, trong đó ABCD là hình bình hành. Chứng minh rằng điểm M đối xứng với điểm N qua điểm C.

Hình 13

Lời giải:

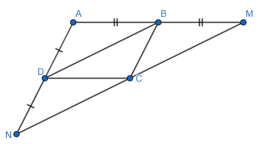
Tứ giác ABCD là hình bình hành:

⇒ AB // CD hay BM // CD.

Xét tứ giác BMCD ta có:

BM // CD

BM = CD( = AB ) (giả thiết)

Suy ra: Tứ giác BMCD là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).

⇒ MC // BD và MC = BD (1)

+) Ta có AD // BC (giả thiết) hay DN // BC.

Xét tứ giác BCND ta có:

DN // BC và DN = BC (vì cùng bằng AD)

Suy ra: Tứ giác BCND là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).

⇒ CN // BD và CN = BD (2).

Từ (1) và (2) theo tiên đề Ơ- clit suy ra: M, C, N thẳng hàng và MC = CN( = BD).

Do đó N đối xứng với M qua C.

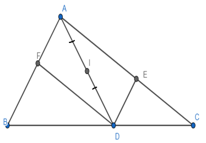
Bài 93 trang 92 SBT Toán 8 Tập 1: Cho hình 14 trong đó DE // AB, DF // AC. Chứng minh rằng điểm E đối xứng với điểm F qua điểm I.

Hình 14

Lời giải:

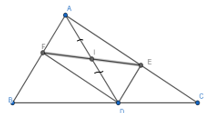
Ta có: DE //AB (giả thiết) hay DE //AF.

Và DF //AC (giả thiết) hay DF //AE.

Suy ra, tứ giác AEDF là hình bình hành.

Lại có, I là trung điểm của AD nên I cũng là trung điểm EF (tính chất hình bình hành)

Vậy E và F đối xứng qua tâm I.

Bài 94 trang 92 SBT Toán 8 Tập 1: Cho tam giác ABC, các đường trung tuyến BM, CN. Gọi D là điểm đối xứng với B qua M, gọi E là điểm đối xứng với C qua N. Chứng minh rằng điểm D đối xứng với điểm E qua điểm A.

Lời giải:

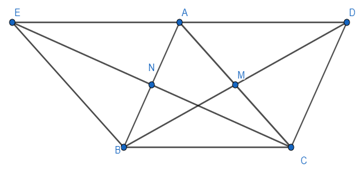
* Xét tứ giác ABCD, ta có:

MA = MC (vì M là trung điểm của AC).

MB = MD (định nghĩa đối xứng tâm).

Suy ra: Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường).

⇒ AD // BC và AD = BC (tính chất hình bình hành) (1)

* Xét tứ giác ACBE, ta có:

AN = NB (Vì N là trung điểm AB)

NC = NE (định nghĩa đối xứng tâm)

Suy ra: Tứ giác ACBE là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)

⇒ AE // BC và AE = BC (tính chất hình bình hành) (2).

Từ (1) và (2) suy ra: A, D, E thẳng hàng và AD = AE.

Nên A là trung điểm của DE hay điểm D đối xứng với điểm E qua điểm A.

Bài 95 trang 92 SBT Toán 8 Tập 1: Cho tam giác ABC vuông tại A, điểm D thuộc cạnh BC. Gọi E là điểm đối xứng với D qua AB, gọi F là điểm đối xứng với D qua AC. Chứng minh rằng các điểm E và F đối xứng với nhau qua điểm A.

Lời giải:

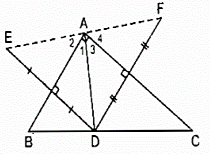
* Vì E đối xứng với D qua AB

⇒ AB là đường trung trực của đoạn thẳng DE

⇒ AD = AE (tính chất đường trung trực)

Nên ΔADE cân tại A.

Suy ra: AB là đường phân giác của $\widehat{DAE}$ 

⇒ $\widehat{A_1}=\widehat{A_2}$.

* Vì F đối xứng với D qua AC

⇒ AC là đường trung trực của đoạn thẳng DF

⇒ AD = AF (tính chất đường trung trực).

Nên ΔADF cân tại A.

Suy ra: AC là phân giác của $\widehat{DAF}$

⇒ $\widehat{A_3}=\widehat{A_4}$

Ta có:

$\begin{array}{l}\widehat{E\text{}A\text{}F}=\widehat{EAD}+\text{\hspace{0.17em}\hspace{0.17em}}\widehat{D\text{}A\text{}F}\\ \\ =\text{\hspace{0.17em}\hspace{0.17em}}\widehat{A_1\text{}}+\widehat{A_2\text{}}+\text{\hspace{0.17em}}\widehat{A_3\text{}}+\text{\hspace{0.17em}}\widehat{A_4}\\ \\ =2(\widehat{A_1\text{}}+\text{\hspace{0.17em}\hspace{0.17em}}\widehat{A_3\text{}})\\ \\ ={2.90}^0={180}^0\end{array}$

⇒ E, A, F thẳng hàng có AE = AF = AD.

Nên A là trung điểm của EF hay điểm E đối xứng với điểm F qua điểm A.

Bài 96 trang 92 SBT Toán 8 Tập 1: Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các cạnh đối AD, BC ở E, F. Chứng minh rằng các điểm E và F đối xứng với nhau qua điểm O.

Lời giải:

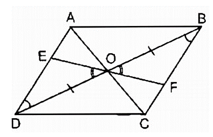
Xét ΔOED và ΔOFB, ta có:

$\widehat{EOD}=\widehat{FOB}$ (đối đỉnh)

OD = OB (tính chất hình bình hành)

$\widehat{ODE}=\widehat{OBF}$ (so le trong)

Do đó: ΔOED = ΔOFB (g.c.g)

⇒ OE = OF.

Vậy O là trung điểm của EF hay điểm E đối xứng với điểm F qua điểm O.

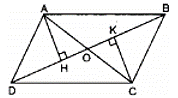
Bài 97 trang 92 SBT Toán 8 Tập 1: Cho hình 15, trong đó ABCD là hình bình hành. Chứng minh H và K đối xứng với nhau qua điểm O.

Lời giải:

Xét hai tam giác vuông AHO và CKO, ta có:

$\widehat{AHO}=\widehat{CKO}$ = 90^o

OA = OC (tính chất hình bình hành)

$\widehat{AOH}=\widehat{COK}$(đối đỉnh)

Suy ra: ΔAHO = ΔCKO (cạnh huyền - góc nhọn).

⇒ OH = OK (hai cạnh tương ứng)

Vậy O là trung điểm của HK hay điểm H đối xứng với điểm K qua điểm O.

Bài 98 trang 92 SBT Toán 8 Tập 1: Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Gọi O là một điểm bất kỳ nằm trong tam giác ABC. Vẽ điểm M đối xứng với O qua D, vẽ điểm N đối xứng với O qua E. Chứng minh rằng MNCB là hình bình hành.

Lời giải:

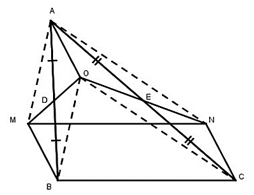
* Xét tứ giác AOBM, ta có:

DA = DB (do D là trung điểm của AB)

DO = DM (định nghĩa đối xứng tâm)

Suy ra: Tứ giác AOBM là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)

⇒ BM // AO và BM = AO (1).

* Xét tứ giác AOCN, ta có:

EA = EC (do E là trung điểm AC)

EO = EN (định nghĩa đối xứng tâm)

Suy ra: Tứ giác AOCN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường).

⇒ CN // AO và CN = AO (2).

Từ (1) và (2) suy ra:

BM // CN và BM = CN.

Vậy tứ giác BMNC là hình bình hành (vì có 1 cặp cạnh đối song song và bằng nhau).

Bài 99 trang 92 SBT Toán 8 Tập 1: Cho tam giác ABC, các đường trung tuyến AD, BE, CF cắt nhau tại G. Gọi H là điểm đối xứng với G qua D, I là điểm đối xứng với G qua E, K là điểm đối xứng với G qua F. Tìm các điểm đối xứng với A, với B, với C qua G.

Lời giải:

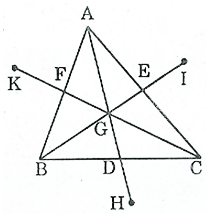
*) Tam giác ABC có ba đường trung tuyến AD, BE, CF cắt nhau tại G nên G là trọng tâm tam giác ABC.

* Ta có: GD = DH (tính chất đối xứng tâm)

⇒ GH = 2GD (l)

GA = 2GD (tính chất đường trung tuyến của tam giác) (2)

Từ (1) và (2) suy ra: GA = GH và A, G, H đều năm trên đường trung tuyến AD

Suy ra điểm đối xứng với điểm A qua G là H.

* Ta có: GE = EI (tính chất đối xứng tâm)

⇒ GI = 2GE (3)

Lại có, GB = 2GE (tính chất đường trung tuyến của tam giác) (4)

Từ (3) và (4) suy ra: GB = GI và G, B, I đều năm trên đường trung tuyến BE

Suy ra điểm đối xứng với điểm B qua G là I.

+) Ta có: GF = FK (tính chất đối xứng tâm)

⇒ GK = 2GF (5)

GC = 2GF (tính chất đường trung tuyến của tam giác) (6)

Từ (5) và (6) suy ra: GC = GK và C; G; K cùng nằm trên đường trung tuyến CF

Suy ra điểm đối xứng với điểm C qua G là điểm K

Bài 100 trang 92 SBT Toán 8 Tập 1: Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Qua O vẽ đường thẳng cắt hai cạnh AB, CD ở E, F. Qua O vẽ đường thẳng cắt hai cạnh AD, BC ở G, H. Chứng minh rằng EGFH là hình bình hành.

Lời giải:

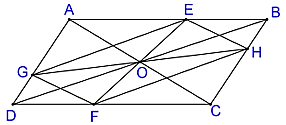
* Xét ΔOAE và ΔOCF, ta có:

OA = OC (tính chất hình bình hành)

$\widehat{AOE}=\widehat{COF}$ (đối đỉnh)

$\widehat{OAE}=\widehat{OCF}$ (so le trong)

Do đó: ΔOAE = ΔOCF (g.c.g)

⇒ OE = OF (l)

* Xét ΔOAG và ΔOCH, ta có:

OA = OC (tính chất hình bình hành)

$\widehat{AOG}=\widehat{COH}$ (đối đỉnh)

$\widehat{OAG}=\widehat{OCH}$ (so le trong).

Do đó: ΔOAG = ΔOCH (g.c.g)

⇒ OG = OH (2)

Từ (1) và (2) suy ra tứ giác EGFH là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường).

Bài 101 trang 92 SBT Toán 8 Tập 1: Cho góc xOy, điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, vẽ điểm C đối xứng với A qua Oy.

a) Chứng minh rằng OB = OC;

b) Tính số đo góc xOy để B đối xứng với C qua O.

Lời giải:

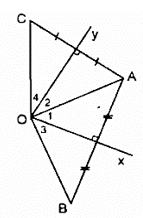
a) Vì B đối xứng với A qua trục Ox nên Ox là đường trung trực của đoạn AB.

⇒ OA = OB (tính chất đường trung trực) (1)

Vì C đối xứng với A qua trục Oy nên Oy là đường trung trực của đoạn AC.

⇒ OA = OC (tính chất đường trung trực) (2)

Từ (l) và (2) suy ra: OB = OC.

b) Vì OB = OC nên để điểm B đối xứng với C qua tâm O cần thêm điều kiện B, O, C thằng hàng

ΔOAB cân tại O có Ox là đường trung trực của AB nên Ox cũng là đường phân giác của $\widehat{AOB}$

 ⇒ $\widehat{O_1}=\widehat{O_3}$ (3)

ΔOAC cân tại O có Oy là đường trung trực của AC nên Oy cũng là đường phân giác của $\widehat{AOC}$

⇒ $\widehat{O_2}=\widehat{O_4}$ (4)

Vì B, O, C thẳng hàng nên:

$\widehat{O_1}+\widehat{O_2}$ $+\widehat{O_3}+\widehat{O_4}$= 180^o (5)

Từ (3),(4) ; (5) ⇒$2\widehat{O_1}+2\widehat{O_2}$ = 180^o

⇒$\widehat{O_1}+\widehat{O_2}$ = 90^o 

⇒ $\widehat{xOy}$ = 90^o

Vậy $\widehat{xOy}$ = 90^o thì B đối xứng với C qua O.

Bài 102 trang 92 SBT Toán 8 Tập 1: Cho tam giác ABC có trực tâm H. Gọi M là trung điểm của BC, K là điểm đối xứng với H qua M. Tính số đo các góc ABK, ACK.

Lời giải:

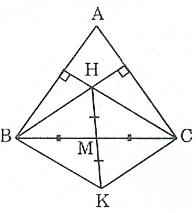
Ta có K là điểm đối xứng của H qua tâm M nên MK = MH.

Xét tứ giác BHCK, ta có:

BM = MC (giả thiết)

MK = MH (chứng minh trên)

Suy ra: Tứ giác BHCK là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường).

Suy ra: KB // CH, KC // BH (tính chất hình bình hành)

Ta có: CH ⊥ AB (giả thiết)

Do đó, KB ⊥ AB nên $\widehat{KBA}$ = 90^o

Ta có: BH ⊥ AC (giả thiết)

Do đó, CK ⊥ AC nên $\widehat{KCA}$ = 90^o

Bài 103 trang 92 SBT Toán 8 Tập 1: Trong các hình sau, hình nào có tâm đối xứng? Với các hình đó, hãy chỉ ra tâm đối xứng của hình.

a) Đoạn thẳng AB.

b) Tam giác đều ABC.

c) Đường tròn tâm O.

Lời giải:

a) Đoạn thẳng AB là hình có tâm đối xứng. Tâm đối xứng của đoạn thẳng AB là trung điểm của nó.

Với C là trung điểm của AB

b) Tam giác đều ABC là hình không có tâm đối xứng.

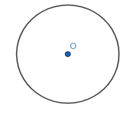
c) Đường tròn tâm O là hình có tâm đối xứng. Tâm đối xứng của (O) là tâm của đường tròn đó.

Bài 104 trang 93 SBT Toán 8 Tập 1: Cho góc xOy và điểm A nằm trong góc đó.

a) Vẽ điểm B đối xứng với O qua A. Qua B vẽ đường thẳng song song với Ox, cắt Oy ở C. Gọi D là giao điểm của CA và Ox. Chứng minh rằng các điểm C và D đối xứng với nhau qua điểm A.

b) Từ đó suy ra cách dựng hình đường thẳng đi qua A, cắt Ox, Oy ở C, D sao cho A là trung điểm của CD.

Lời giải:

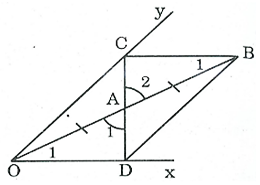
a) Xét ΔOAD và ΔBAC, ta có:

OA = AB (tính chất đối xứng tâm)

$\widehat{A_1}=\widehat{A_2}$(đối đỉnh)

$\widehat{O_1}=\widehat{B_1}$(so le trong)

Do đó: ΔOAD = ΔBAC (g.c.g)

⇒ AD = AC.

Suy ra: C đối xứng với D qua A.

b) Cách dựng:

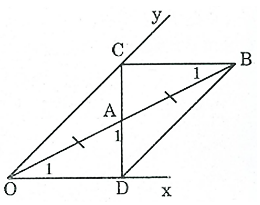
- Dựng B đối xứng với O qua A.

- Qua B dựng đường thẳng song song Ox cắt Oy tại C.

- Dựng tia CA cắt Ox tại D.

Ta có D là điểm cần dựng.

Chứng minh:

Xét ΔOAD và ΔBAC, ta có:

OA = AB (tính chất đối xứng tâm)

$\widehat{A_1}=\widehat{A_2}$(đối đỉnh)

$\widehat{O_1}=\widehat{B_1}$ (so le trong)

Do đó: ΔOAD = ΔBAC (g.c.g)

⇒ AD = AC

Suy ra: C đối xứng với D qua A.

Bài 105 trang 93 SBT Toán 8 Tập 1: Cho tam giác ABC, điểm M nằm trên cạnh BC. Gọi O là trung điểm của AM. Dựng điểm E thuộc cạnh AB, điểm F thuộc cạnh AC sao cho E đối xứng với F qua O.

Lời giải:

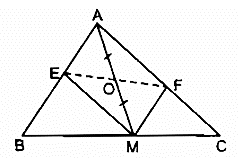
Cách dựng:

- Qua điểm M dựng đường thẳng song song với AC cắt AB tại E.

- Qua điểm M dựng đường thẳng song song với AB cắt AC tại F.

Chứng minh:

Ta có: ME // AC hay ME // AF.

Và MF //AB hay MF // AE

Suy ra: tứ giác AEMF là hình bình hành.

Ta có: O là trung điểm của AM

Suy ra: EF đi qua O (tính chất hình bình hành)

⇒ OE = OF

Vậy E đối xứng với F qua tâm O.

Bài tập bổ sung

Bài 8.1 trang 93 SBT Toán 8 Tập 1: Xét tính đúng – sai của mỗi khẳng định sau: a) Trung điểm của một đoạn thẳng...

Bài 8.2 trang 93 SBT Toán 8 Tập 1: Cho tam giác ABC, đường trung tuyến AM và trọng tâm G. Gọi I là điểm đối xứng với A qua G...

Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:

Bài 9: Hình chữ nhật

Bài 10: Đường thẳng song song với một đường thẳng cho trước

Bài 11: Hình thoi

Bài 12: Hình vuông

Ôn tập chương 1 - Phần Hình học

Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

Trắc nghiệm Đối xứng tâm có đáp án