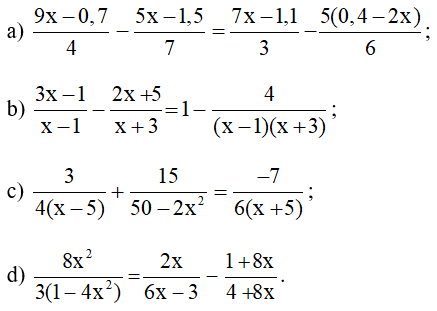SBT Toán 8 Ôn tập chương 3 - Phần Đại số

Mục lục Giải SBT Toán 8 Ôn tập chương 3 - Phần Đại số

Bài 62 trang 16 SBT Toán 8 Tập 2: Cho hai biểu thức $A=\frac{5}{2m+1}$ và $B=\frac{4}{2m-1}$. Hãy tìm các giá trị của m để hai biểu thức ấy có giá trị thỏa mãn hệ thức:

a) 2A + 3B = 0;

b) A.B = A + B.

Lời giải:

Ta có: $A=\frac{5}{2m+1}$ và $B=\frac{4}{2m-1}$

ĐKXĐ: $m\ne \pm \frac{1}{2}$

a) Ta có: 2A + 3B = 0 khi

$\begin{array}{l}2.\frac{5}{2m+1}+\text{\hspace{0.17em}\hspace{0.17em}}3.\frac{4}{2m-1}=0\\ \iff \frac{10}{2m+1}+\frac{12}{2m-1}=0\\ \iff \frac{10(2m-1)}{(2m+1)(2m-1)}+\frac{12(2m+1)}{(2m-1)(2m+1)}=0\end{array}$

 $\Rightarrow$10(2m – 1) + 12(2m + 1) = 0

⇔ 20m – 10 + 24m + 12 = 0

⇔ 44m + 2 = 0

⇔ $m=\frac{-1}{22}$ (thỏa mãn)

Vậy $m=\frac{-1}{22}$ thì 2A + 3B = 0.

b)Để AB =  A+ B thì:

$\begin{array}{l}\frac{5}{2m+1}.\frac{4}{2m-1}=\frac{5}{2m+1}+\frac{4}{2m-1}\\ \iff \frac{20}{(2m+1)(2m-1)}\\ =\frac{5(2m-1)}{(2m-1)(2m+1)}+\frac{4(2m+1)}{(2m-1)(2m+1)}\end{array}$

 $\Rightarrow$20 = 5(2m – 1) + 4(2m + 1)

⇔ 20 = 10m – 5 + 8m + 4

⇔ 18m = 21

⇔ $m=\frac{7}{6}$ (thỏa mãn )

Vậy $m=\frac{7}{6}$ thì A.B = A + B.

Bài 63 trang 16 SBT Toán 8 Tập 2: Tính gần đúng nghiệm của các phương trình sau, làm tròn đến chữ số thập phân thứ hai (dùng máy tính bỏ túi để tính toán).

a) $\left(x\sqrt{13}\text{\hspace{0.17em}}+\text{}\sqrt{5}\right).\left(\sqrt{7}-x\sqrt{3}\right)=0$ ;

b) $\left(x\sqrt{2,7}-1,54\right).\left(\sqrt{1,02}+x\sqrt{3,1}\right)=0$.

Lời giải:

a)

$\begin{array}{l}\left(x\sqrt{13}\text{\hspace{0.17em}}+\text{}\sqrt{5}\right).\left(\sqrt{7}-x\sqrt{3}\right)=0\\ \iff \left[\begin{array}{c}x\sqrt{13}\text{\hspace{0.17em}}+\text{}\sqrt{5}=0\\ \sqrt{7}-x\sqrt{3}=0\end{array}\right.\end{array}$

Nếu

$$\begin{gathered} x\sqrt{13}\text{\hspace{0.17em}}+\text{}\sqrt{5}=0\iff x\sqrt{13}\text{\hspace{0.17em}}=-\text{\hspace{0.17em}}\sqrt{5} \\ \iff x=\frac{-\sqrt{5}}{\sqrt{13}}\approx -0,62 \end{gathered}$$

Nếu $\sqrt{7}-x\sqrt{3}=0\iff x=\frac{\sqrt{7}}{\sqrt{3}}\approx 1,53$

Vậy phương trình có nghiệm x = – 0,62; x = 1,53

b)

$\begin{array}{l}\left(x\sqrt{2,7}-1,54\right).\left(\sqrt{1,02}+x\sqrt{3,1}\right)=0\\ \iff \left[\begin{array}{c}x\sqrt{2,7}-1,54=0\\ \sqrt{1,02}+x\sqrt{3,1}=0\end{array}\right.\end{array}$

Nếu

$$\begin{gathered} \sqrt{1,02}+x\sqrt{3,1}=0 \\ \iff x=\frac{-\sqrt{1,02}}{\sqrt{3,1}}\approx -0,57 \end{gathered}$$

Nếu

$$\begin{gathered} x\sqrt{2,7}-1,54=0 \\ \iff x=\frac{1,54}{\sqrt{2,7}}\approx 0,94 \end{gathered}$$

Vậy phương trình có nghiệm x = 0,94; x = – 0,57.

Bài 64 trang 16 SBT Toán 8 Tập 2: Giải các phương trình sau:

Lời giải:

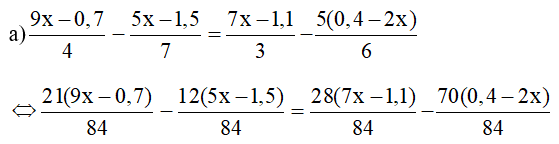
⇔ 21(9x – 0,7) – 12(5x – 1,5)

= 28(7x – 1,1) – 70(0,4 – 2x)

⇔ 189x – 14,7 – 60x + 18

= 196x – 30,8 – 28 + 140x

⇔ 189x – 60x – 196x – 140x

= – 30,8 – 28 + 14,7 – 18

⇔ – 207x = – 62,1 ⇔ x = 0,3

Vậy phương trình có nghiệm x = 0,3.

b) $\frac{3x-1}{x-1}-\frac{2x+\text{}5}{x+3}=1-\frac{4}{(x-1)(x+\text{\hspace{0.17em}}3)}$ 

 (ĐKXĐ: $x\ne 1;x\ne -3$)

$$\begin{gathered} \iff \frac{(3x-1)(x+3)}{(x-1)(x+3)}-\frac{(2x+\text{}5)(x-1)}{(x+3)(x-1)} \\ =\frac{(x+3)(x-1)}{(x+3)(x-1)}-\frac{4}{(x-1)(x+\text{\hspace{0.17em}}3)} \end{gathered}$$

 $\Rightarrow$(3x – 1)(x + 3) – (2x + 5)(x – 1)

= (x – 1)(x + 3) – 4

⇔ 3x² + 9x – x – 3 – 2x² + 2x – 5x + 5

= x² + 3x – x – 3 – 4

⇔ 3x² – 2x² – x² + 9x – x + 2x – 5x – 3x + x = – 3 – 4 + 3 – 5

⇔ 3x = – 9 ⇔ x = – 3 (loại)

Vậy phương trình vô nghiệm.

c) $\frac{3}{4(x-5)}+\text{\hspace{0.17em}\hspace{0.17em}}\frac{15}{50-2x^2}=\frac{-7}{6(x+5)}$   (ĐKXĐ: $x\ne \pm 5$)

$\begin{array}{l}\iff \frac{3}{4(x-5)}-\text{\hspace{0.17em}\hspace{0.17em}}\frac{15}{2(x^2-25)}=\frac{-7}{6(x+5)}\\ \iff \frac{3.3(x+5)}{12(x-5)(x+\text{}5)}-\text{\hspace{0.17em}\hspace{0.17em}}\frac{15.6}{12(x-5)(x+5)}\\ \hspace{0.17em}=\frac{-7.2(x-5)}{12(x+5)(x-5)}\end{array}$

 $\Rightarrow$9(x + 5) – 90 = – 14(x – 5)

⇔ 9x + 45 – 90 = – 14x + 70

⇔ 9x + 14x = 70 – 45 + 90

⇔ 23x = 115 ⇔ x = 5 (loại)

Vậy phương trình vô nghiệm.

d) $\frac{8x^2}{3(1-4x^2)}=\frac{2x}{6x-3}-\frac{1+8x}{4+\text{}8x}$       (ĐKXĐ: $x\ne \pm \frac{1}{2}$)

$\iff \frac{8x^2}{3(1-4x^2)}-\frac{2x}{6x-3}+\frac{1+8x}{4+\text{}8x}=0$

$\iff \frac{8x^2}{3(1-4x^2)}+\frac{2x}{3-6x}+\frac{1+8x}{4+\text{}8x}=0$

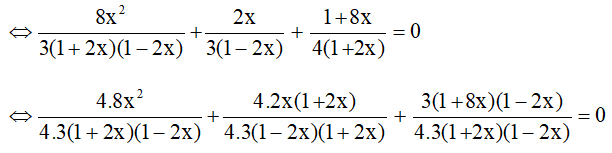
 32x² + 8x(1 + 2x) + 3(1 + 8x)(1 – 2x) = 0

⇔ 32x² + 8x + 16x² + 3 + 18x – 48x² = 0

⇔ 32x² + 16x² – 48x² + 18x + 8x = – 3

⇔ 26x = – 3 ⇔ $x=\frac{-3}{26}$ (thỏa mãn)

Vậy phương trình có nghiệm $x=\frac{-3}{26}$ .

Bài 65 trang 16 SBT Toán 8 Tập 2: Cho phương trình (ẩn x): 4x² – 25 + k² + 4kx = 0.

a) Giải phương trình với k = 0.

b) Giải phương trình với k = – 3.

c) Tìm các giá trị của k sao cho phương trình nhận x = – 2 làm nghiệm.

Lời giải:

a) Khi k = 0 ta có phương trình:

4x² – 25 = 0

⇔ (2x + 5)(2x – 5) = 0

⇔ 2x + 5 = 0 hoặc 2x – 5 = 0

Nếu 2x + 5 = 0 ⇔ $x=\frac{-5}{2}$

Nếu 2x – 5 = 0 ⇔ $x=\frac{5}{2}$

Vậy phương trình có nghiệm

$x=\frac{-5}{2}$ hoặc $x=\frac{5}{2}$.

b) Khi k = – 3 ta có phương trình:

4x² – 25 + (– 3)² + 4.(– 3)x = 0

⇔ 4x² – 25 + 9 – 12x = 0

⇔ 4x² – 12x – 16 = 0

⇔ x² – 3x – 4 = 0

⇔ x² – 4x + x – 4 = 0

⇔ x(x – 4) + (x – 4) = 0

⇔ (x + 1)(x – 4) = 0

⇔ x + 1 = 0 hoặc x – 4 = 0

Nếu x + 1 = 0 ⇔ x = – 1

Nếu x – 4 = 0 ⇔ x = 4

Vậy phương trình có nghiệm

x = – 1; x = 4.

c) Phương trình nhận x = – 2 làm nghiệm nên ta có:

4.(– 2)² – 25 + k² + 4k.(– 2) = 0

⇔ 16 – 25 + k² – 8k = 0

⇔ k² – 8k – 9 = 0

⇔ k² – 9k + k – 9 = 0

⇔ k(k – 9) + (k – 9) = 0

⇔ (k + 1)(k – 9) = 0

⇔ k + 1 = 0 hoặc k – 9 = 0

Nếu k + 1 = 0 ⇔ k = –1

Nếu k – 9 = 0 ⇔ k = 9

Vậy k = – 1 hoặc k = 9 thì

phương trình nhận x = – 2 làm nghiệm.

Bài 66 trang 17 SBT Toán 8 Tập 2: Giải các phương trình sau:

a) (x + 2)(x² – 3x + 5) = (x + 2)x² ;

b) $\frac{-7x^2+4}{x^3+1}=\frac{5}{x^2-x+1}-\frac{1}{x+1}$;

c) 2x² – x = 3 – 6x;

d) $\frac{x-2}{x+2}-\frac{3}{x-2}=\frac{2(x-11)}{x^2-4}$.

Lời giải:

a) (x + 2)(x² – 3x + 5) = (x + 2)x²

⇔ (x + 2)(x² – 3x + 5) – (x + 2)x² = 0

⇔ (x + 2)[(x² – 3x + 5) – x²] = 0

⇔ (x + 2)(x² – 3x + 5 – x²) = 0

⇔ (x + 2)(5 – 3x) = 0

⇔ x + 2 = 0 hoặc 5 – 3x = 0

Nếu x + 2 = 0 ⇔ x = – 2

Nếu 5 – 3x = 0 ⇔ x = $\frac{5}{3}$.

Vậy phương trình có nghiệm

x = – 2; $x=\frac{5}{3}$.

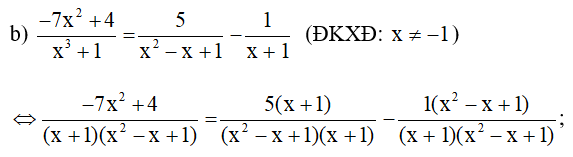
 $\Rightarrow$– 7x² + 4 = 5x + 5 – x² + x – 1

⇔ – 7x² + x² – 5x – x = 5 – 1 – 4

⇔ – 6x² – 6x = 0

⇔ – x² – x = 0

⇔ x(x + 1) = 0

⇔ x = 0 hoặc x + 1 = 0

⇔ x = 0 hoặc x = – 1 (loại vì không thỏa mãn ĐK)

Vậy phương trình có nghiệm x = 0.

c)  2x² – x = 3 – 6x

⇔ 2x² – x + 6x – 3 = 0

⇔ (2x² + 6x) – (x + 3) = 0

⇔ 2x(x + 3) – (x + 3) = 0

⇔ (2x – 1)(x + 3) = 0

⇔ 2x – 1 = 0 hoặc x + 3 = 0

Nếu 2x – 1 = 0 ⇔ $x=\frac{1}{2}$.

Nếu x + 3 = 0 ⇔ x = – 3

Vậy phương trình có nghiệm $x=\frac{1}{2}$; x = – 3.

d) $\frac{x-2}{x+2}-\frac{3}{x-2}=\frac{2(x-11)}{x^2-4}$              (ĐKXĐ: $x\ne \pm 2$)

$$\begin{gathered} \iff \frac{(x-2)(x-2)}{(x+2)(x-2)}-\frac{3(x+2)}{(x-2)(x+\text{}2)} \\ =\frac{2(x-11)}{(x+2)(x-2)} \end{gathered}$$

 $\Rightarrow$(x – 2)(x – 2) – 3(x + 2) = 2x – 22

⇔ x² – 2x – 2x + 4 – 3x – 6 = 2x – 22

⇔ x² – 2x – 2x – 3x – 2x + 4 – 6 + 22 = 0

⇔ x² – 9x + 20 = 0

⇔ x² – 5x – 4x + 20 = 0

⇔ x(x – 5) – 4(x – 5) = 0

⇔ (x – 4)(x – 5) = 0

⇔ x – 4 = 0 hoặc x – 5 = 0

Nếu x – 4 = 0 ⇔ x = 4 (t/m)

Nếu x – 5 = 0 ⇔ x = 5 (t/m)

Vậy phương trình có nghiệm x = 4 hoặc x = 5.

Bài 67 trang 17 SBT Toán 8 Tập 2: Số nhà của Khanh là một số tự nhiên có hai chữ số. Nếu thêm chữ số 5 vào bên trái số đó thì được một số kí hiệu là A. Nếu thêm chữ số 5 vào bên phải số đó thì được một số kí hiệu là B. Tìm số nhà của Khanh, biết rằng A – B = 153.

Lời giải:

Gọi x là, số nhà bạn Khanh.

Điều kiện: x ∈ N* và 9 < x < 100.

Thêm số 5 vào bên trái số nhà bạn Khanh ta được:

$A\text{}=\overline{5x}=500+\text{\hspace{0.17em}}x$ (vì x là số có 2 chữ số).

Thêm số 5 vào bên phải số nhà bạn Khanh ta được:

$B\text{}=\overline{x5}=\overline{x0}+5=10x+5$

Vì hiệu của A – B = 153 nên ta có phương trình:

(500 + x) – (10x + 5) = 153

⇔ 500 + x – 10x – 5 = 153

⇔ – 9x = 153 – 500 + 5

⇔ – 9x = – 342 ⇔ x = 38 (thỏa mãn)

Vậy số nhà bạn Khanh là 38.

Bài 68 trang 17 SBT Toán 8 Tập 2: Một đội thợ mỏ lập kế hoạch khai thác than, theo đó mỗi ngày phải khai thác được 50 tấn than. Khi thực hiện, mỗi ngày đội khai thác được 57 tấn than. Do đó, đội đã hoàn thành kế hoạch trước một ngày và còn vượt mức 13 tấn than. Hỏi theo kế hoạch, đội phải khai thác bao nhiêu tấn than?

Lời giải:

Gọi x (tấn) là khối lượng than khai thác theo kế hoạch. ĐK: x > 0.

Thời gian dự định làm là $\frac{x}{50}$ (ngày)

Khối lượng than thực tế khai thác là x + 13 (tấn)

Thời gian thực tế làm là $\frac{x+13}{57}$ (ngày)

Vì thời gian hoàn thành sớm hơn kế hoạch một ngày nên ta có phương trình:

$$\begin{gathered} \frac{x}{50}-\frac{x+13}{57}=1 \\ \iff \frac{57x}{2850}-\frac{50(x+13)}{2850}=\frac{2850}{2850} \end{gathered}$$

⇔ 57x – 50x – 650 = 2850

⇔ 7x = 2850 + 650

⇔ 7x = 3500

⇔ x = 500 (thỏa mãn)

Vậy theo kế hoạch, đội phải khai thác 500 tấn than.

Bài 69 trang 17 SBT Toán 8 Tập 2: Hai xe ô tô cùng khởi hành từ Lạng Sơn và Hà Nội, quãng đường dài 163km. Trong 43km đầu, hai xe cùng vận tốc. Nhưng sau đó chiếc xe thứ nhất tăng vận tốc lên gấp 1,2 lần vận tốc ban đầu, trong khi đó xe thứ hai vẫn duy trì vận tốc cũ. Do đó xe thứ nhất đến Hà Nội sớm hơn xe thứ hai là 40 phút. Tính vận tốc ban đầu của hai xe.

Lời giải:

Gọi x (km/h) là vận tốc ban đầu của hai xe. Điều kiện: x > 0.

Quãng đường còn lại sau khi xe thứ nhất tăng vận tốc là:

163 – 43 = 120 (km)

Vận tốc xe thứ nhất sau khi tăng tốc là 1,2x (km/h)

Thời gian xe thứ nhất đi hết quãng đường còn lại là $\frac{120}{1,2x}$ (giờ)

Thời gian xe thứ hai đi hết quãng đường còn lại là $\frac{120}{x}$ (giờ)

Vì xe thứ nhất đến sớm hơn xe thứ hai 40 phút = $\frac{2}{3}$ giờ nên ta có phương trình:

$\begin{array}{l}\frac{120}{x}-\frac{120}{1,2x}=\frac{2}{3}\\ \iff \frac{120}{x}-\frac{100}{x}=\frac{2}{3}\\ \iff \frac{360}{3x}-\frac{300}{3x}=\frac{2x}{3x}\end{array}$

$\Rightarrow$ 360 – 300 = 2x

⇔ 2x = 60 ⇔ x = 30 (thỏa mãn )

Vậy vận tốc ban đầu của hai xe là 30km/h.

Bài 70 trang 17 SBT Toán 8 Tập 2: Một đoàn tàu hỏa từ Hà Nội đi thành phố Hồ Chí Minh. 1 giờ 48 phút sau, một tàu hỏa khác khởi hành từ Nam Định đi thành phố Hồ Chí Minh với vận tốc nhỏ hơn vận tốc của đoàn tàu thứ nhất là 5km/h. Hai đoàn tàu gặp nhau (tại một ga nào đó) sau 4 giờ 48 phút kể từ khi đoàn tàu thứ nhất khởi hành. Tính vận tốc của mỗi tàu biết rằng ga Nam Định nằm trên đường từ Hà Nội đi thành phố Hồ Chí Minh và cách Hà Nội 87km.

Lời giải:

Gọi x (km/h) là vận tốc của đoàn tàu thứ hai. Điều kiện: x > 0.

Vận tốc của đoàn tàu thứ nhất là x + 5 (km/h)

Khi gặp nhau thì đoàn tàu thứ nhất đi được 4 giờ 48 phút.

Vì đoàn tàu thứ hai đi sau 1 giờ 48 phút nên đoàn tàu thứ hai đi được 3 giờ

Thời gian đoàn tàu thứ nhất đi được khi hai tàu gặp nhau là:

4 giờ 48 phút = $\frac{24}{5}$ giờ

Quãng đường đoàn tàu thứ hai đi được từ lúc khởi hành đến lúc hai đoàn tàu gặp nhau là 3x (km)

Quãng đường đoàn tàu thứ nhất đi được từ lúc khởi hành đến lúc hai đoàn tàu gặp nhau là $\frac{24}{5}$ (x + 5) (km)

Theo đề bài ta có phương trình:

$\frac{24}{5}(x+\text{}5)=3x+87$

$\begin{array}{l}\iff \frac{24}{5}x+\text{\hspace{0.17em}}24=3x+87\\ \iff \frac{9x}{5}=63\iff x=35\left(tm\right)\end{array}$

Vận tốc của đoàn tàu thứ hai là 35km/h, vận tốc của đoàn tàu thứ nhất là 35 + 5 = 40 (km/h).

Bài 71 trang 17 SBT Toán 8 Tập 2: Lúc 7h sáng, một ca nô xuôi dòng từ bến A đến bến B, cách nhau 36km rồi ngay lập tức quay trở về và đến bến A lúc 11 giờ 30 phút. Tính vận tốc của ca nô khi xuôi dòng, biết rằng vận tốc của nước chảy là 6km/h.

Lời giải:

Gọi x (km/h) là vận tốc thực của ca nô. Điều kiện: x > 6

Vận tốc của ca nô khi xuôi dòng là x + 6 (km/h)

Vận tốc của ca nô khi ngược dòng là x – 6 (km/h)

Thời gian lúc ca nô đi xuôi dòng là $\frac{36}{x+6}$ (giờ)

Thời gian lúc ca nô đi ngược dòng là $\frac{36}{x-6}$ (giờ)

Thời gian ca nô đi và về:

11 giờ 30 phút – 7 giờ = 4 giờ 30 phút = $\frac{9}{2}$ giờ

Theo đề bài, ta có phương trình:

$\begin{array}{l}\frac{36}{x+6}+\frac{36}{x-6}=\frac{9}{2}\\ \iff \frac{36.2(x-6)}{2(x+6)(x-6)}+\frac{36.2(x+\text{}6)}{2(x-6)(x+\text{}6)}\\ =\frac{9(x+\text{}6)(x-6)}{2(x+\text{}6)(x-6)}\end{array}$

 $\Rightarrow$72(x – 6) + 72(x + 6) = 9(x + 6)(x – 6)

⇔ 72x – 432 + 72x + 432 = 9x² – 324

⇔ 9x² – 144x – 324 = 0

⇔ x² – 16x – 36 = 0

⇔ x² + 2x – 18x – 36 = 0

⇔ x(x + 2) – 18(x + 2) = 0

⇔ (x + 2)(x – 18) = 0

⇔ x + 2 = 0 hoặc x – 18 = 0

Nếu  x + 2 = 0 ⇔ x = – 2 < 0 (loại).

Nếu x – 18 = 0 ⇔ x = 18 (thỏa mãn).

Vậy vận tốc thực của ca nô là 18km/h, suy ra vận tốc của ca nô lúc xuôi dòng là 18 + 6 = 24 (km/h).

Bài tập bổ sung

Bài III.1 trang 18 SBT Toán 8 Tập 2: Giải các phương trình sau...

Bài III.2 trang 18 SBT Toán 8 Tập 2: a) Cho ba số a, b và c đôi một phân biệt. Giải phương trình...

Bài III.3 trang 18 SBT Toán 8 Tập 2: Cần phải thêm vào tử và mẫu của phân số $\frac{13}{18}$ với cùng một số tự nhiên nào để được...

Bài III.4 trang 18 SBT Toán 8 Tập 2: Cách đây 10 năm, tuổi của người thứ nhất gấp 3 lần tuổi của người thứ hai...

Xem thêm lời giải sách bài tập Toán học lớp 8 hay, chi tiết khác:

Bài 1: Liên hệ giữa thứ tự và phép cộng

Bài 2: Liên hệ giữa thứ tự và phép nhân

Bài 3: Bất phương trình một ẩn

Bài 4: Bất phương trình bậc nhất một ẩn

Bài 5: Phương trình chứa dấu giá trị tuyệt đối

Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

Lý thuyết Ôn tập chương 3

Trắc nghiệm Bài ôn tập Chương 3 có đáp án