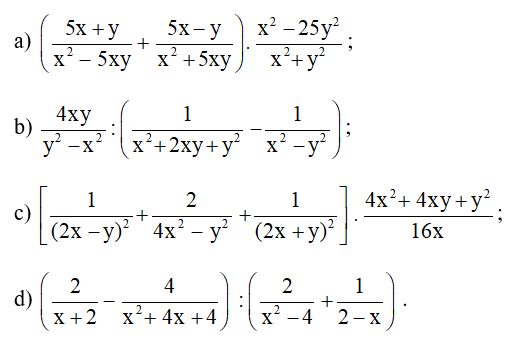SBT Toán 8 Bài 9: Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
Với giải sách bài tập Toán lớp 8 Bài 9: Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức chi tiết được Giáo viên nhiều năm kinh nghiệm biên soạn bám sát nội dung sách bài tập Toán 8 Tập 1 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8.
Mục lục Giải SBT Toán 8 Bài 9: Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
Bài 44 trang 36 SBT Toán 8 Tập 1: Biến đổi các biểu thức sau thành phân thức:
Lời giải:
a) 12 + x1− x x+ 2 = 12 + x x+2− x x+ 2
= 12+ x2x+2 = 12 + x(x+2)2
= 1+x(x+2)2= 1+x2+2x2=(x+1)22
b) x− 1x21+ 1x + 1x2
=(x− 1x2) : (1+ 1x + 1x2)
= x3−1x2 : x2+ x+ 1x2
= x3−1x2. x2x2+ x+ 1= (x3−1)x2x(x2+ x+ 1)2= (x−1)(x2+x+1)x2x(x2+ x+ 1)2 = x−1
c) 1− 2yx + y2x2 1x − 1y
= (1− 2yx + y2x2): (1x − 1y)
= x2−2xy+ y2x2 : y−xxy
= (x−y)2x2. xyy−x = (x−y)2xyx2.[−(x−y)] = (x−y)yx.(−1) = −(x−y)yx=y(y−x)x
d) x4− 1+ 34xx2 − 6x + 12
= (x4− 1+ 34x) : (x2 − 6x + 12)= x2−4x+ 34x : x2−12+ x2x
= x2−4x+ 34x. 2xx2−12+ x= (x2−4x+ 3).2x4x(x2−12+ x) = (x2−x)−(3x−3)2[(x−29)+(x−3)]
= x(x−1)−3(x−1)2[(x+3)(x−3)+ (x−3)] = (x−3)(x−1)2(x+3+1)(x−3)
= (x−3)(x−1)2(x+4)(x−3)= x−12(x+4)
Bài 45 trang 36 SBT Toán 8 Tập 1: Thực hiện các phép tính sau:
Lời giải:
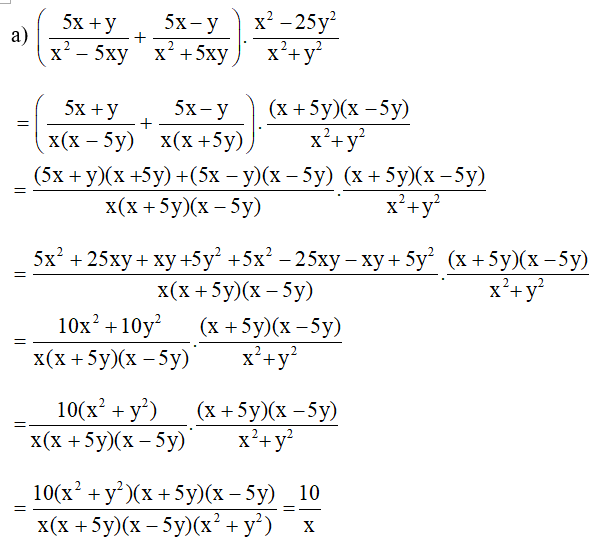
b) 4xyy2− x2: (1x2+ 2xy + y2 − 1x2− y2)
= 4xyy2− x2: (1(x+y)2 − 1(x+y)(x− y))= −4xyx2− y2 : 1(x−y)−1.(x+y)(x+y)2(x−y)
= −4xy(x+y)(x−y) : −2y(x+y)2(x−y)= −4xy(x+y)(x−y). (x+y)2(x−y)−2y
= −4xy.(x+y)2(x−y) (x+y)(x−y)(−2y) = 2x(x+y)
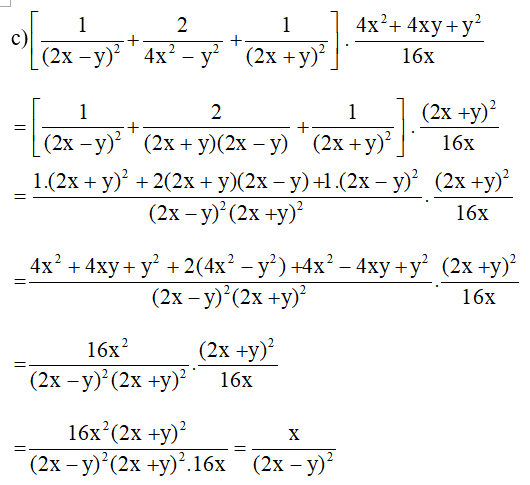
d) (2x+ 2− 4x2+ 4x+ 4) : (2x2− 4 + 12−x)
=(2x+ 2−4(x+2)2): (2(x+2)(x−2)−1x−2)= 2(x+2)− 4(x+2)2 : 2−1.(x+2)(x+2)(x− 2)
= 2x(x+2)2 : −x(x+2)(x− 2)= 2x(x+2)2. (x+2)(x−2)−x
= 2x(x+2)(x−2)(x+2)2(−x) = −2(x−2)x+2=2(2−x)x+2
Bài 46 trang 36 SBT Toán 8 Tập 1: Tìm điều kiện của biến để giá trị của phân thức xác định:
Lời giải:
a) Phân thức: 5x2−4x+ 220 xác định với mọi x∈ℝ (vì 20 ≠ 0).
b) Phân thức: 8x+ 2004 xác định khi
x + 2004 ≠ 0 ⇒ x ≠ - 2004.
c) Phân thức: 4x3x− 7 xác định khi
3x – 7 ≠ 0 ⇒x≠73.
d) Phân thức: x2x+ z xác định khi
Lời giải:
a) 52x− 3x2= 5x(2−3x) xác định khi:
x(2−3x)≠0⇒{x≠02−3x≠0⇒{x≠0x≠23
Vậy phân thức 52x− 3x2 xác định với x ≠ 0 và x≠23.
b) 2x8x3+ 12x2+ 6x+ 1= 2x(2x+ 1)3 xác định khi (2x + 1)3 ≠ 0
Suy ra: 2x + 1 ≠ 0 ⇒x≠−12.
c) −5x216−24x+ 9x2= −5x2(4−3x)2 xác định khi:
(4 – 3x)2 ≠ 0 ⇒ 4 – 3x ≠ 0 ⇒x≠43.
d) 3x2−4y2= 3(x+2y).(x−2y) xác định khi:
(x – 2y)(x + 2y) ≠ 0
⇒{x+ 2y ≠0x−2y ≠0 ⇒{x ≠−2yx≠2y⇒x≠±2y
Bài 48 trang 37 SBT Toán 8 Tập 1: Có bạn nói rằng các phân thức 2x2x−2; 1x2−2x+ 1; 5x3(x−1).(x2+1) có cùng điều kiện biến x. Điều đó đúng hay sai? Vì sao?
Lời giải:
Ta có: 2x2x−2 xác định khi
2x – 2 ≠ 0 ⇒ 2x ≠ 2 ⇒ x ≠ 1
1x2−2x+ 1=1(x−1)2 xác định khi
(x – 1)2 ≠ 0 ⇒ x – 1 ≠ 0 ⇒ x ≠ 1
5x3(x−1).(x2+1) xác định khi
(x – 1)(x2 + 1) ≠ 0 hay x – 1 ≠ 0
(vì với mọi x thì x2 ≥ 0 nên x2 + 1 > 0)
Do đó, phân thức 5x3(x−1).(x2+1) xác định với x ≠ 1.
Vậy các phân thức 2x2x−2; 1x2−2x+ 1; 5x3(x−1).(x2+1) có cùng điều kiện biến x là đúng.
Bài 49 trang 37 SBT Toán 8 Tập 1: a) Tìm một phân thức (một biến) mà giá trị của nó được xác định với mọi giá trị của biến khác các số nguyên lẻ lớn hơn 5 và nhỏ hơn 10.
b) Tìm một phân thức (một biến) mà giá trị của nó được xác định với mọi giá trị của biến khác ±√2.
Lời giải:
a)
+) Tập hợp các số nguyên lẻ lớn hơn 5 và nhỏ hơn 10 là: {7; 9}.
+) Do đó, phân thức cần tìm xác định với x ≠ 7; x ≠ 9 .
Suy ra: x – 7 ≠ 0 và x – 9 ≠ 0
Ta chọn phân thức là 1(x− 7).(x−9).
b) Phân thức một biến mà giá trị của nó được xác định với mọi giá trị của biến khác ±√2 nên x≠√2 và x≠− √2.
Suy ra: x− √2 ≠0 và x+ √2 ≠ 0 ta chọn phân thức:
a(x+ √2).(x−√2)= ax2−2
Bài 50 trang 37 SBT Toán 8 Tập 1: Đố. Đố em tìm được một cặp phân thức của biến x mà khi giá trị của phân thức này bằng 0 thì giá trị của phân thức kia không xác định và ngược lại khi giá trị phân thức kia bằng 0 thì giá trị phân này không xác định. Em tìm được bao nhiêu cặp như thế?
Lời giải:
Ta chỉ cần tìm hai phân thức là nghịch đảo của nhau với tử và mẫu đều chứa biến x và không có giá trị nào của x để tử và mẫu đồng thời bằng 0.
Ví dụ: x+ 2x−5 và x−5x+ 2.
Có vô số cặp phân thức như vậy.
Bài 51 trang 37 SBT Toán 8 Tập 1: Tính giá trị của các biểu thức:
a) 3x2−x9x2−6x+ 1 tại x = – 8;
b) x2+ 3x+ 2x3+ 2x2− x−2 tại x = 1 000 001.
Lời giải:
a) ĐKXĐ: 9x2 – 6x + 1 ≠ 0 ⇒ (3x – 1)2 ≠ 0
⇒x≠13
Ta có x = – 8 ≠13 thỏa mãn ĐKXĐ.
3x2−x9x2−6x+ 1= x(3x−1)(3x−1)2= x3x−1
Thay x = – 8 vào biểu thức, ta có:
−83.(−8)−1= −8−24−1= 825
b) Ta có:
x3 + 2x2 – x – 2 = x2(x + 2) – (x + 2)
= (x2 – 1). (x + 2) = (x + 1).(x – 1)(x + 2)
Do đó, phân thức đã cho xác định khi
x3 + 2x2 – x – 2 ≠ 0 hay
(x + 2)(x – 1)(x + 1) ≠ 0
⇒ x ≠ – 2 và x ≠ ± 1
Ta có: x = 1 000 001 thỏa mãn điều kiện.
x2+ 3x+ 2x3+ 2x2− x−2= x2+ 2x+ x+ 2(x+2)(x−1).(x+ 1)= (x+ 2).(x+ 1)(x+ 2)(x−1)(x+ 1)= 1x−1
Thay x = 1 000 001 vào biểu thức ta được:
Bài 52 trang 37 SBT Toán 8 Tập 1: Tìm điều kiện của các biến trong mỗi phân thức sau đây. Chứng minh rằng khi giá trị của phân thức xác định thì giá trị đó không phụ thuộc vào các biến x và y (nghĩa là chứng tỏ rằng có thể biến đổi phân thức đã cho thành một biểu thức không chứa x và y):
b) 2ax −2x−3y+3ay4ax + 6x +9y+ 6ay
Lời giải:
a) x2− y2(x+ y)(6x−6y) xác định khi:
(x + y)(6x – 6y) ≠ 0 .
Suy ra:
{x+ y≠06x− 6y≠0⇒{x≠−yx− y≠0⇒{x≠−yx≠ y
Điều kiện x ≠ ± y, ta có:
x2− y2(x+ y)(6x−6y)= (x+ y).(x−y)(x+ y).6.(x−y)= 16
Vậy biểu thức không phụ thuộc vào x, y.
b) 2ax −2x−3y+3ay4ax + 6x +9y+ 6ay xác định khi
4ax + 6x + 9y + 6ay ≠ 0
⇒ 2x(2a + 3) + 3y(2a + 3)
= (2a + 3)(2x + 3y) ≠ 0
Suy ra:
{2a+ 3≠02x + 3y≠0 ⇔{a≠−32x≠−3y2.
Điều kiện: x≠−32y và a≠−32
2ax −2x−3y+3ay4ax + 6x +9y+ 6ay= 2x(a−1)+ 3y(a−1)(2a+3).(2x+3y)
= (2x+3y).(a−1)(2a+ 3).(2x+3y)= a−12a+ 3
Vậy biểu thức không phụ thuộc vào x, y.
Lời giải:
Điều kiện: x3 – 2x2 = x2(x – 2) ≠ 0 ⇒ x ≠ 0 và x ≠ 2
Ta có:
4x2− 4x3 + x4x3 −2x2= x2(x2−4x+ 4)x2(x−2)= x2(x−2)2x2(x−2)= x−2
a) Nếu phân thức đã cho bằng – 2 thì biểu thức x – 2 cũng có giá trị bằng – 2.
Suy ra: x – 2 = – 2 ⇒ x = 0 không thỏa mãn điều kiện.
Vậy không có giá trị nào của x để phân thức bằng – 2.
b) Nếu phân thức đã cho bằng 2 thì biểu thức x – 2 cũng có giá trị bằng 2.
Suy ra: x – 2 = 2 ⇒ x = 4.
Với x = 4 thỏa mãn điều kiện.
Vậy khi x = 4 thì phân thức có giá trị bằng 2.
c) Nếu phân thức có giá trị bằng 0 thì biểu thức x – 2 cũng có giá trị bằng 0.
Suy ra: x – 2 = 0 ⇒ x = 2 mà x = 2 không thỏa mãn điều kiện.
Vậy không có giá trị nào của x để phân thức có giá trị bằng 0.
Bài 54 trang 37 SBT Toán 8 Tập 1: Cho biểu thức x2+2x2x+ 10 + x−5x + 50−5x 2x(x + 5).
a) Tìm điều kiện của biến x để giá trị của biểu thức được xác định.
b) Tìm giá trị của x để giá trị của biểu thức bằng 1.
c) Tìm giá trị của x để giá trị của biểu thức bằng -12.
d) Tìm giá trị của x để giá trị của biểu thức bằng – 3.
Lời giải:
a) Biểu thức xác định khi
2x + 10 ≠ 0, x ≠ 0 và 2x(x + 5) ≠ 0
Suy ra điều kiện xác định: x ≠ 0 và x ≠ – 5.
Ta có:
x2+2x2x+ 10 + x−5x + 50−5x 2x(x + 5)
= x(x+ 2)2(x+ 5) + x−5x + 50−5x2x(x+5)
= x2(x+ 2)2x(x+ 5) + (x−5).2(x+5)x.2(x+ 5) + 50−5x2x(x+5)
= x2(x+ 2)+ (x−5).2.(x+ 5)+ 50− 5x2x(x+ 5)
= x3+2x2+2x2−50 + 50−5x2x(x+ 5)
= x3+ 4x2 −5x2x(x+ 5)= x(x2+ 4x− 5)2x(x+ 5)
= x(x−1)(x+ 5)2x(x+ 5)= x− 12
b) Nếu giá trị phân thức bằng 1 thì giá trị của biểu thức x−12 cũng bằng 1.
Suy ra: x−12=1 ⇒ x – 1 = 2 ⇒ x = 3
mà x = 3 thỏa mãn điều kiện.
Vậy x = 3 thì giá trị của phân thức bằng 1.
c) Nếu giá trị phân thức bằng -12 thì giá trị của biểu thức x−12 cũng bằng -12
Suy ra: x−12= −12 ⇒ x – 1 = – 1
⇒ x = 0 mà x = 0 không thỏa mãn điều kiện.
Vậy không có giá trị nào của x để phân thức bằng −12 .
d) Nếu giá trị phân thức bằng – 3 thì giá trị của biểu thức x−12 cũng bằng – 3.
Suy ra: x−12= -3 ⇒ x – 1 = – 6
⇒ x = – 5 mà x = – 5 không thỏa mãn điều kiện.
Vậy không có giá trị nào của x để phân thức bằng – 3.
Bài 55 trang 38 SBT Toán 8 Tập 1: Tìm x, biết:
a) 2x+ 1x2− 2x+ 1− 2x+ 3x2 −1 = 0;
b) 3x− 3 − 6x9−x2 + xx+ 3 =0.
Lời giải:
a) 2x+ 1x2− 2x+ 1− 2x+ 3x2 −1 = 0 (điều kiện )
2x+ 1(x−1)2− 2x+ 3(x+1 )(x−1)= 0(2x+ 1)(x+ 1)−(2x+3)(x−1)(x−1)2(x+ 1)=0
2x2+2x+x+ 1−(2x2−2x+ 3x− 3)(x−1)2(x+1)=0
2x2+2x+x+ 1−2x2+2x− 3x+ 3(x−1)2(x+ 1)=0
2x+ 4(x−1)2.(x+1)=0
Biểu thức bằng 0 khi tử bằng 0 và mẫu khác 0
Ta có: 2x + 4 = 0 nên x = – 2 (thỏa mãn điều kiện)
Vậy với x = – 2 thì giá trị của biểu thức bằng 0.
b) 3x− 3 − 6x9−x2 + xx+ 3 =0 (điều kiện )
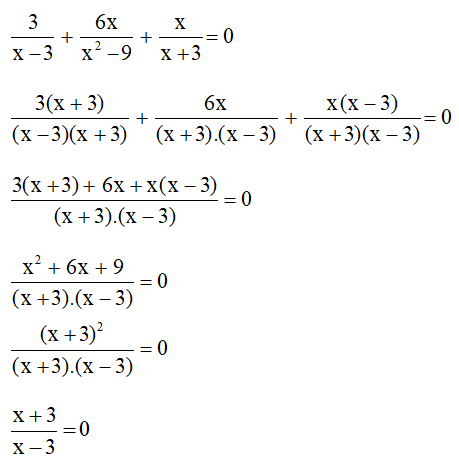
Biểu thức bằng 0 khi tử bằng 0 và mẫu khác 0
Ta có: x + 3 = 0 nên x = – 3 (không thỏa mãn điều kiện)
Vậy không có giá trị nào của x để biểu thức bằng 0.
Bài 56 trang 38 SBT Toán 8 Tập 1: Với giá trị nào của x thì giá trị của mỗi biểu thức sau bằng 0:
Lời giải:
a) Biểu thức xác định khi:
x2 – 4 = (x + 2).(x – 2) ≠ 0
và (x + 2)2 ≠ 0 hay x ≠ ± 2 .
Ta có:
xx2−4 + 3(x+ 2)2= x(x+2).(x−2) + 3(x+ 2)2
= x(x+ 2)+ 3(x−2)(x+ 2)2.(x−2)= x2+ 2x+ 3x−6(x+ 2)2.(x−2)
=x2+ 5x−6(x+ 2)2(x−2)= x2−x+ 6x−6(x+ 2)2(x−2)= x(x−1)+ 6(x−1)(x+ 2)2.(x−2) = (x−1)(x+ 6)(x+ 2)2.(x−2)
Biểu thức bằng 0 khi (x – 1)(x + 6) = 0
và (x – 2)(x + 2)2 ≠ 0
+) Ta có: (x – 1).(x + 6) = 0
khi x – 1= 0 hay x + 6 = 0
x – 1 = 0 khi x = 1 (thỏa mãn điều kiện)
x + 6 = 0 khi x = – 6 (thỏa mãn điều kiện)
Vậy với x = 1 hoặc x = – 6 thì giá trị biểu thức bằng 0.
b) 1x2+ x+ 1 + x−1
= 1+ (x− 1).(x2+ x+ 1)x2+ x+ 1
= 1+ x3−1x2+ x+ 1= x3x2+ x+ 1
Biểu thức bằng 0 khi
x3 = 0 và x2 + x + 1 ≠ 0
Ta có: x3 = 0 ⇒ x = 0;
x2+x+1=x2+ 2.x. 12+ 14 + 34 = (x+ 12)2+ 34 >0 với mọi x
Vậy với x = 0 thì giá trị của biểu thức bằng 0.
Bài 57 trang 38 SBT Toán 8 Tập 1: Tìm giá trị nguyên của biến x để tại đó giá trị của mỗi biểu thức sau là một số nguyên:
Lời giải:
a) Vì 2x−3 là một số nguyên
nên 2 ⁝ (x – 3) và x ≠ 3
Suy ra: x – 3 ∈ Ư(2) = {– 2; – 1; 1; 2}
Ta có: x – 3 = – 2
⇒ x = 1 (t/m x là số nguyên)
x – 3 = – 1 ⇒ x = 2 (t/m)
x – 3 = 1 ⇒ x = 4 (t/m)
x – 3 = 2 ⇒ x = 5 (t/m)
Vậy với x ∈ {1; 2; 4; 5} thì 2x−3 là một số nguyên.
b) Vì 3x+ 2 là một số nguyên
nên 3 ⁝ (x + 2) và x ≠ – 2
Suy ra: x + 2 ∈ Ư(3) = {– 3; – 1; 1; 3}
Ta có: x + 2 = – 3 ⇒ x = – 5;
x + 2= – 1 ⇒ x = – 3;
x + 2 = 1 ⇒ x = – 1;
x + 2 = 3 ⇒ x = 1
Vậy với x ∈ {– 5; – 3; – 1; 1}
thì 3x+ 2 là một số nguyên.
c) Ta có:
3x3−4x2+ x−1x−4
= (3x2+ 8x+ 33)(x−4)+ 131x− 4
=3x2+ 8x+ 33+ 131x−4
Với x là số nguyên ta có:
3x2 + 8x + 33 là số nguyên.
Để biểu thức đã cho là số nguyên thì 131 ⁝ (x – 4) và x ≠ 4
Suy ra: x – 4 ∈ Ư(131)
= {– 131; – 1; 1; 131}
Ta có: x – 4 = – 131 ⇒ x = – 127;
x – 4 = – 1 ⇒ x = 3;
x – 4 = 1 ⇒ x = 5;
x – 4 = 131 ⇒ x = 135
Vậy với x ∈ {– 127; 3; 5; 135}
thì 3x3−4x2+ x−1x−4 là số nguyên.
d) Ta có: 3x2−x+ 13x+ 2
= (3x+ 2).(x−1)+33x+ 2= x−1+ 33x+ 2
(với x≠− 23).
Vì x là số nguyên nên x – 1 là số nguyên.
Để biểu thức đã cho là số nguyên
thì 3 ⁝ (3x + 2) và x≠− 23.
Suy ra: 3x + 2 ∈ Ư(3) = {– 3; – 1; 1; 3}
Ta có: 3x + 2 = – 3 ⇒ x= −53 ∉ℤ(loại)
3x + 2 = – 1 ⇒ x = – 1 (thỏa mãn)
3x + 2 = 1 ⇒ x= −13 ∉ℤ(loại)
3x + 2 = 3 ⇒ x= 13 ∉ℤ (loại)
Vậy với x = – 1 thì 3x2−x+ 13x+ 2 có giá trị nguyên.
Bài tập bổ sung
Bài 9.1 trang 39 SBT Toán 8 Tập 1: Biết rằng...
Xem thêm lời giải sách bài tập Toán học lớp 8 hay, chi tiết khác:
Bài 5: Phép cộng các phân thức đại số
Bài 6: Phép trừ các phân thức đại số
Bài 7: Phép nhân các phân thức đại số
Bài 8: Phép chia các phân thức đại số
Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:
Lý thuyết Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
Trắc nghiệm Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức có đáp án
Xem thêm các chương trình khác:
- Tóm tắt tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 8 (hay nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Soạn văn 8 (ngắn nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Văn mẫu lớp 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Hóa học 8
- Giải sbt Hóa học 8
- Giải vở bài tập Hóa học 8
- Lý thuyết Hóa học 8
- Các dạng bài tập Hóa học lớp 8
- Giải sgk Vật Lí 8
- Giải sbt Vật Lí 8
- Lý thuyết Vật Lí 8
- Giải vở bài tập Vật lí 8
- Giải sgk Tiếng Anh 8 (sách mới) | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2
- Giải sgk Tiếng Anh 8 | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2 (sách mới)
- Giải sbt Tiếng Anh 8 (sách mới) | Sách bài tập Tiếng Anh 8
- Giải sbt Tiếng Anh 8 (thí điểm)
- Giải sgk Tin học 8 | Giải bài tập Tin học 8 Học kì 1, Học kì 2 (sách mới)
- Giải sgk Lịch Sử 8 | Giải bài tập Lịch sử 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Lịch sử 8 (sách mới) | Kiến thức trọng tâm Lịch sử 8
- Giải vở bài tập Lịch sử 8
- Giải Tập bản đồ Lịch sử 8
- Đề thi Lịch Sử 8
- Giải vở bài tập Sinh học 8
- Giải sgk Sinh học 8
- Lý thuyết Sinh học 8
- Giải sgk Giáo dục công dân 8 | Giải bài tập Giáo dục công dân 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Giáo dục công dân 8 (sách mới) | Kiến thức trọng tâm GDCD 8
- Lý thuyết Địa Lí 8 (sách mới) | Kiến thức trọng tâm Địa Lí 8
- Giải sgk Địa Lí 8 | Giải bài tập Địa Lí 8 Học kì 1, Học kì 2 (sách mới)
- Giải Tập bản đồ Địa Lí 8
- Đề thi Địa lí 8