Lý thuyết Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức (mới 2023 + Bài Tập) – Toán 8
Lý thuyết Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức lớp 8 gồm lý thuyết chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm Toán 8 Bài 9: Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức.
A. Lý thuyết
1. Biểu thức hữu tỉ
Mỗi biểu thức là một phân thức hoặc biểu thị một dãy phép toán cộng, trừ, nhân, chia trên những phân thức gọi là biểu thức hữu tỉ.
Ví dụ. Ta có các biểu thức hữu tỉ như: ; …
2. Biến đổi một biểu thức hữu tỉ thành một phân thức
Nhờ các quy tắc của các phép toán cộng, trừ, nhân, chia các phân thức, ta có thể biến đổi các biểu thức hữu tỉ thành một phân thức.
Ví dụ. Biến đổi biểu thức thành một phân thức.
Hướng dẫn giải:
Ta có:
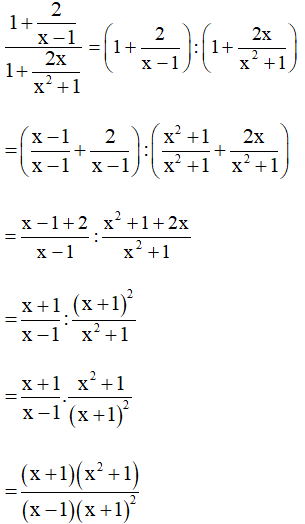
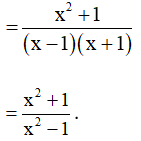
3. Giá trị của phân thức
Khi thực hiện các bài toán liên quan đến giá trị của phân thức:
+ Trước hết, phải tìm điều kiện của biến để giá trị tương ứng của mẫu thức khác 0: Điều kiện của biến để giá trị tương ứng của mẫu thức khác 0 là điều kiện để giá trị của phân thức được xác định.
+ Nếu tại giá trị của biến mà giá trị của phân thức được xác định thì phân thức ấy và phân thức được rút gọn có cùng một giá trị.
Để tính giá trị của phân thức, ta chỉ cần thay giá trị của biến vào phân thức đã được rút gọn rồi thực hiện tính như tính giá trị của biểu thức số.
Ví dụ. Cho phân thức .
a) Tìm điều kiện của x để giá trị của phân thức được xác định.
b) Tính giá trị của phân thức tại x = 2020.
Hướng dẫn giải:
a) Giá trị của phân thức được xác định với điều kiện x(x – 2) ≠ 0.
Mà một tích (của nhiều số) khác 0 khi mọi thừa số đều khác 0, do đó x ≠ 0 và x – 2 ≠ 0 hay chính là x ≠ 0 và x ≠ 2.
Vậy điều kiện để giá trị của phân thức được xác định là: x ≠ 0 và x ≠ 2.
b) Ta có: và x = 2020 thỏa mãn các điều kiện của biến nên có thể tính giá trị của phân thức đã cho bằng cách tính giá trị của phân thức rút gọn .
Vậy giá trị của phân thức đã cho tại x = 2020 bằng .
B. Bài tập tự luyện
Bài 1. Giá trị của phân thức được xác định khi nào?
Hướng dẫn giải:
Ta có: phân thức xác định khi x2 – 4 ≠ 0.
Mà x2 – 4 = (x – 2)(x + 2)
Nên (x – 2)(x + 2) ≠ 0
Mà một tích khác 0 khi mọi thừa số đều khác 0.
Do đó: x – 2 ≠ 0 và x + 2 ≠ 0
Hay x ≠ 2 và x ≠ – 2.
Vậy giá trị của phân thức được xác định khi x ≠ 2 và x ≠ – 2.
Bài 2. Tìm giá trị của x để giá trị phân thức bằng 0.
Hướng dẫn giải:
Điều kiện xác định của phân thức là x3 – 4x ≠ 0.
Mà x3 – 4x = x(x2 – 4) = x. (x – 2).(x + 2)
Nên x.(x – 2) . (x + 2) ≠ 0
Suy ra x ≠ 0, x – 2 ≠ 0 và x + 2 ≠ 0.
Hay x ≠ 0, x ≠ 2 và x ≠ – 2.
Ta có:
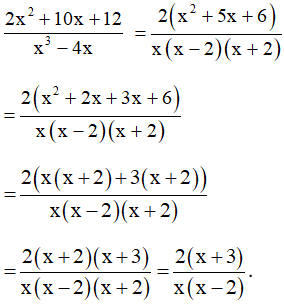
Ta có phân thức bằng 0 khi .
Suy ra 2(x + 3) = 0 ⇒ x = – 3 (thỏa mãn điều kiện).
Vậy x = – 3 thì giá trị phân thức bằng 0.
Bài 3. Biến đổi biểu thức thành phân thức đại số.
Hướng dẫn giải:
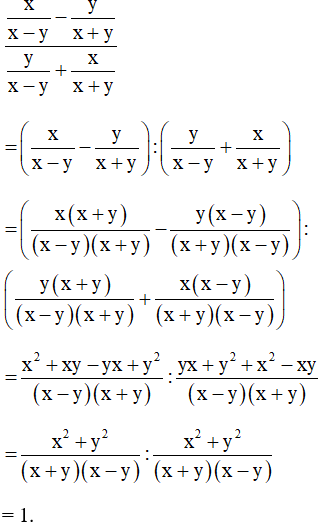
Bài 4. Cho .
a) Rút gọn N;
b) Tính giá trị của N tại x = 15.
Hướng dẫn giải:
a) Ta có: x2 – 7x + 10 = x2 – 2x – 5x + 10 = x(x – 2) – 5(x – 2) = (x – 2)(x – 5)
x2 – 4 = (x + 2)(x – 2)
Do đó điều kiện xác định của biểu thức N là
Hay x – 2 ≠ 0, x + 2 ≠ 0, x – 5 ≠ 0.
Suy ra x ≠ 2, x≠ – 2 và x ≠ 5.
Ta có
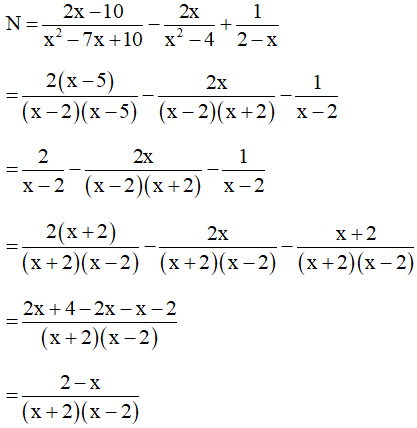
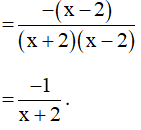
Vậy với x ≠ 2, x≠ – 2 và x ≠ 5.
b) Có x = 15 thỏa mãn các điều kiện của biến x.
Khi đó thay x = 15 vào N ta được:
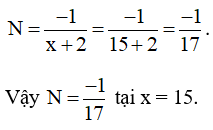
Trắc nghiệm Toán 8 Bài 9: Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
Bài 1: Biến đổi biểu thức thành biểu thức đại số
A.
B. x + 1
C. x – 1
D.
Đáp án: D
Giải thích:
Ta có
=
=
Bài 2: Thực hiện phép tính sau
, ta được kết quả là:
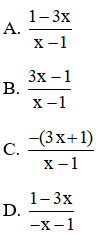
Đáp án: A
Giải thích:
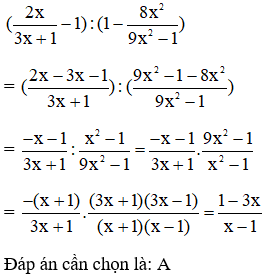
Bài 3: Cho B =.
Số giá trị của x Z để B Z là:
A. 3
B. 0
C. 2
D. -2
Đáp án: C
Giải thích:
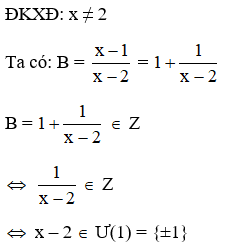
|
x - 2 |
1 |
-1 |
|
x |
3 (t/m) |
1 (t/m) |
Bài 4: Biết A =
Điền biểu thức thích hợp vào ô trống
A.
B. x+ 1
C. x
D. 1
Đáp án: D
Giải thích:
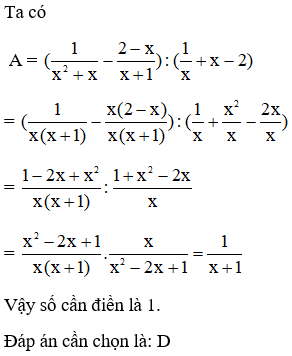
Bài 5: Cho N =
với x là một số nguyên. Chọn câu đúng.
A. Giá trị của N luôn là số nguyên
B. Giá trị của N luôn là số nguyên dương
C. Giá trị của N luôn bằng 0
D. Giá trị của N luôn không âm
Đáp án: A
Giải thích:
ĐK x ≠ 2
Đặt x – 1 = t.
Ta có x = t +1; x – 2 = t – 1
Do đó
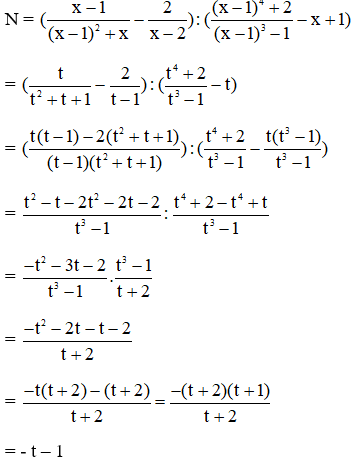
Thay x – 1 = t ta được
N = -(x – 1) – 1 = -x
Vì x là số nguyên nên giá trị của N cũng luôn là số nguyên
Bài 6: Trong trường hợp biểu thức A có nghĩa
thì B =
Điều biểu thức thích hợp vào chỗ trống.
A. -x + 2
B. x – 2
C. -x – 2
D. x + 2
Đáp án: C
Giải thích:
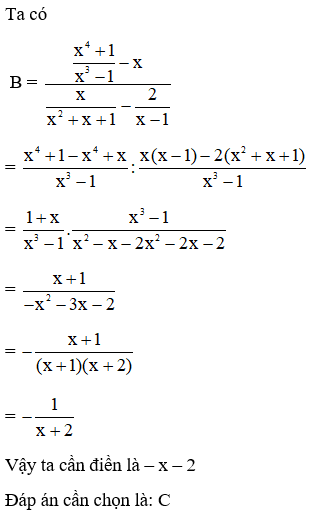
Bài 7: Cho biểu thức B =
Với giá trị nào của x thì B xác định
A. x ≠ {0; 2}
B. x ≠ {-2; 0; 2}
C. x ≠ {-2; 2}
D. x ≠ {0; 2}
Đáp án: B
Giải thích:
Phân thức B =
xác định khi
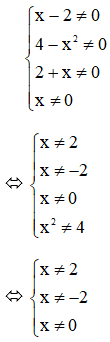
Bài 8: Cho biểu thức B =
Rút gọn B ta được
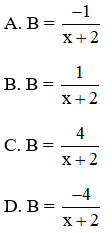
Đáp án: D
Giải thích:
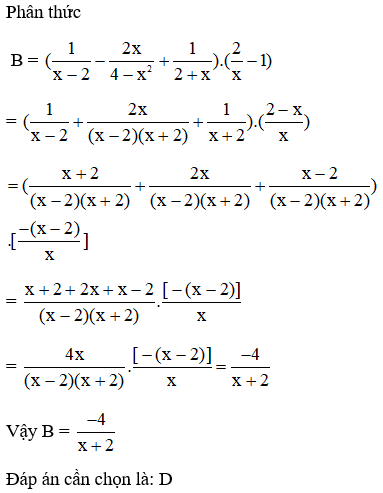
Bài 9: Cho P =
Tìm xZ để P + 1Z
A. x {-23; -5; -3; 15}
B. x{-23; -5; -3}
C. x{5; -5; -3; 15}
D. x{-23; 15}
Đáp án: A
Giải thích:
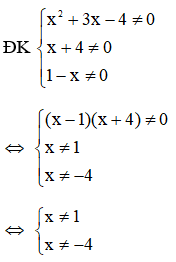
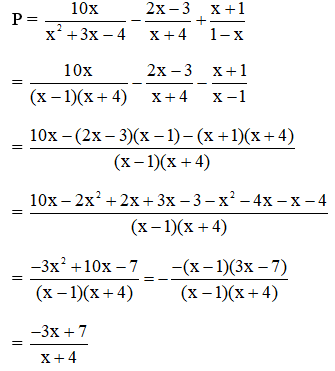
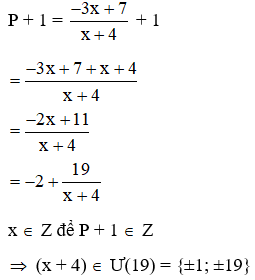
|
x + 4 |
-1 |
1 |
-19 |
19 |
|
x |
-5(tm) |
-3 (tm) |
-23 (tm) |
15(tm) |
|
P + 1 |
-21 |
17 |
-3 |
-1 |
Vậy x {-23; -5; -3; 15} thì P + 1 Z
Bài 10: Cho biểu thức
N =
Rút gọn N ta được
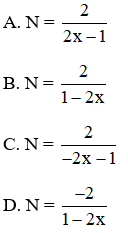
Đáp án: B
Giải thích:
Phân thức
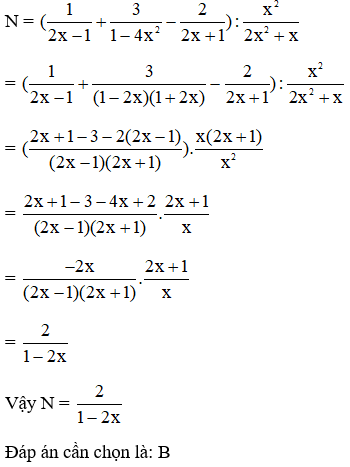
Xem thêm các chương trình khác:
- Tóm tắt tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 8 (hay nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Soạn văn 8 (ngắn nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Văn mẫu lớp 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Hóa học 8
- Giải sbt Hóa học 8
- Giải vở bài tập Hóa học 8
- Lý thuyết Hóa học 8
- Các dạng bài tập Hóa học lớp 8
- Giải sgk Vật Lí 8
- Giải sbt Vật Lí 8
- Lý thuyết Vật Lí 8
- Giải vở bài tập Vật lí 8
- Giải sgk Tiếng Anh 8 (sách mới) | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2
- Giải sgk Tiếng Anh 8 | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2 (sách mới)
- Giải sbt Tiếng Anh 8 (sách mới) | Sách bài tập Tiếng Anh 8
- Giải sbt Tiếng Anh 8 (thí điểm)
- Giải sgk Tin học 8 | Giải bài tập Tin học 8 Học kì 1, Học kì 2 (sách mới)
- Giải sgk Lịch Sử 8 | Giải bài tập Lịch sử 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Lịch sử 8 (sách mới) | Kiến thức trọng tâm Lịch sử 8
- Giải vở bài tập Lịch sử 8
- Giải Tập bản đồ Lịch sử 8
- Đề thi Lịch Sử 8
- Giải vở bài tập Sinh học 8
- Giải sgk Sinh học 8
- Lý thuyết Sinh học 8
- Giải sgk Giáo dục công dân 8 | Giải bài tập Giáo dục công dân 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Giáo dục công dân 8 (sách mới) | Kiến thức trọng tâm GDCD 8
- Lý thuyết Địa Lí 8 (sách mới) | Kiến thức trọng tâm Địa Lí 8
- Giải sgk Địa Lí 8 | Giải bài tập Địa Lí 8 Học kì 1, Học kì 2 (sách mới)
- Giải Tập bản đồ Địa Lí 8
- Đề thi Địa lí 8
