Nội dung bài viết

    Xem thêm

    Lý thuyết Diện tích xung quanh của hình lăng trụ (mới 2023 + Bài Tập) – Toán 8

    Lý thuyết Diện tích xung quanh của hình lăng trụ lớp 8 gồm lý thuyết chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm Toán 8 Bài 5: Diện tích xung quanh của hình lăng trụ.

    1 2,192 25/02/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Lý thuyết Toán 8 Bài 5: Diện tích xung quanh của hình lăng trụ

    Bài giảng Toán 8 Bài 5: Diện tích xung quanh của hình lăng trụ

    A. Lý thuyết

    1. Công thức tính diện tích xung quanh

    Diện tích xung quanh của hình lăng trụ đứng bằng chu vi đáy nhân với chiều cao:

    Sxq = 2p.h    (p: nửa chu vi đáy, h: chiều cao)

    Diện tích toàn phần của hình lăng trụ đứng bằng tổng diện tích xung quanh và diện tích hai đáy.

    Stp = Sxq + S2day     

    Ví dụ 1. Cho hình lăng trụ đứng có đáy là lục giác đều cạnh 6cm, chiều cao lăng trụ là 4cm. Tính diện tích xung quanh của hình lăng trụ?

    Lời giải:

    Do đáy của hình lăng trụ là lục giác đều cạnh 6cm nên chu  vi đáy là:

    P = 6. 6 = 36cm

    Diện tích xung quanh của hình lăng trụ là; 

    Sxq = P.  h = 36.4 = 144 cm2

    B. Bài tập tự luyện

    Bài 1. Cho hình lăng trụ đứng ABCD.MNPQ có đáy ABCD là hình chữ nhật, AB = 6cm; BC = 4cm, chiều cao h = 3cm. Diện tích xung quanh và diện tích toàn phần của hình lăng trụ đứng là?

    Lời giải:

    Ta có nửa chu vi của đáy là:

    p = AB + BC = 6 + 4 = 10 cm

    Diện tích xung quanh của hình lăng trụ đứng là:

    Sxq = 2ph = 2. 10.3 = 60cm2

    Diện tích 1 đáy là: S = AB. BC =6.4 = 24 cm2

    Diện tích toàn phần của hình lăng trụ đứng là:

    Stp = 60 + 2.24 = 108 cm2

    Bài 2. Cho hình lăng trụ đứng đáy là tam giác có độ dài ba cạnh đáy là 4 cm, 6cm  và  8cm. Biết diện tích xung quanh bằng 90cm2. Tính chiều cao của hình lăng trụ?

    Lời giải:

    Chu vi đáy là:  P = 4 + 6+ 8 = 18cm

    Diện tích xung quanh của hình lăng trụ đứng

    Sxq = P.h nên chiều cao:

    h=SxqP=9018=5cm

    Vậy chiều cao của hình trụ là 5cm.

    Bài 3. Tính chiều cao của hình lăng trụ đứng ABCD.EFGH, biết rằng đáy ABCD là hình thoi có các đường chéo AC = 10cm; BD = 24cm và diện tích toàn phần bằng 1280 cm2

    Lời giải:

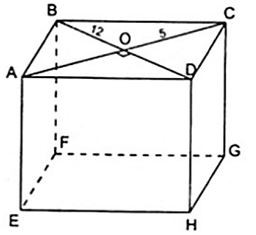
    Lý thuyết Diện tích xung quanh của hình lăng trụ chi tiết – Toán lớp 8 (ảnh 1)

    Diện  tích 1 đáy của hình lăng trụ là:

    S=12AC.BD=120cm2cm2

    Mà Stp = Sxq + S2day

    Nên diện tích xung quanh của hình lăng trụ là:

    Sxq = Stp – S2day = 1280 – 2.120 = 1040 cm2

    Vì đáy ABCD là hình thoi nên AC vuông góc với BD tại trung điểm O (tính chất về đường chéo của hình thoi).

    Ta có BO=12BD=12cm; OC=12AC=5cm.

    Áp dụng định lý Py – ta – go vào tam giác BOC vuông tại O ta được:

    BC2 = BO2 + OC2 = 122 + 52 = 169 nên BC = 13cm

    Chu vi đáy là P = 4.13 = 52cm

    Áp dụng công thức

    Sxq=2p.h⇒h=Sxq2p=104052=20cm

    Chiều cao của hình đã cho là 20 cm.

    Trắc nghiệm Toán 8 Bài 5: Diện tích xung quanh hình lăng trụ

    Bài 1: Cho hình lăng trụ tam giác đều ABC. A’B’C’ có chiều cao bằng 2 cm,  = 450. Tính diện tích xung quanh của hình lăng trụ.

    A. 15 cm2

    B. 6 cm2 

    C. 12 cm2

    D. 16 cm2

    Đáp án: C

    Giải thích:

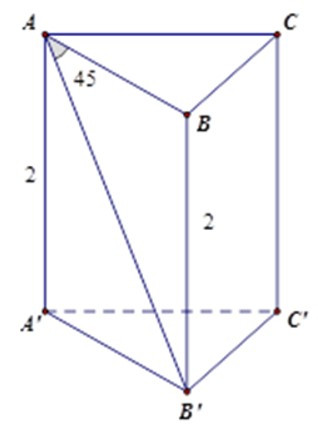
    Trắc nghiệm Diện tích xung quanh hình lăng trụ đứng có đáp án - Toán lớp 8 (ảnh 2)

    Tam giác vuông ABB’ có BAB'^ = 450 nên là tam giác vuông cân tại B

    nên AB = BB’ = 2 cm.

    Vì tam giác ABC đều nên chu vi bằng 3AB = 3.2 = 6 cm

    Diện tích xung quanh bằng 6.2 = 12 (cm2)

    Bài 2: Một hình lăng trụ đứng có đáy là hình chữ nhật có các kích thước 3 cm, 8 cm. Chiều cao của hình lăng trụ đứng là 2 cm. Người ta bọc hình hộp chữ nhật đó bằng giấy. Tính diện tích giấy cần bọc đủ cái hộp ( biết độ dài của đáy không đáng kể)

    A. 44cm2

    B. 48cm2

    C. 96cm2

    D. 68cm2

    Đáp án: C

    Giải thích:

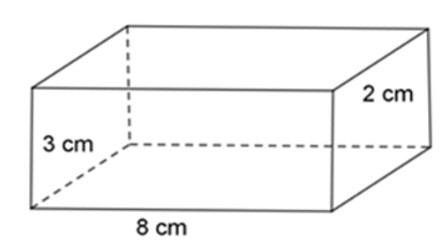
    Trắc nghiệm Diện tích xung quanh hình lăng trụ đứng có đáp án - Toán lớp 8 (ảnh 4)

    Diện tích xung quanh của hình hộp là:

    Diện tích hai đáy là:

    Diện tích giấy cần để bọc cái hộp:

    Bài 3: Tính diện tích xung quanh của hình lăng trụ đứng ngũ giác với các kích thước được đo bằng mét.

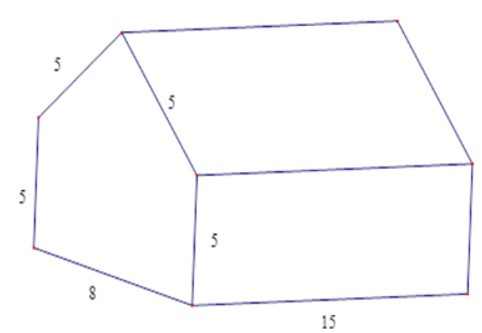
    Trắc nghiệm Diện tích xung quanh hình lăng trụ đứng có đáp án - Toán lớp 8 (ảnh 5)

    A. 375m2

    B. 420m2

    C. 475m2

    D. 320m2

    Đáp án: B

    Giải thích:

    Diện tích xung quanh của hình lăng trụ ngũ giác là:

    5.15.4+8.15=420 m2

    Bài 4: Một nhà kho có dạng hình lăng trụ đứng ngũ giác với các kích thước được đo bằng mét. Hãy tính chiều cao của hình lăng trụ, biết diện tích xung quanh của hình đó bằng

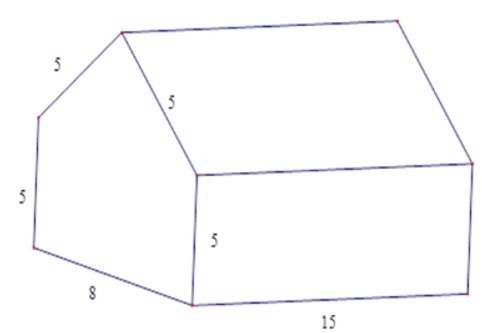
    Trắc nghiệm Diện tích xung quanh hình lăng trụ đứng có đáp án - Toán lớp 8 (ảnh 7)

    A. 15m

    B. 20m

    C. 30m           

    D. 25m

    Đáp án: B

    Giải thích:

    Gọi chiều cao của hình lăng trụ là x (m) điều kiện x>0.

    Diện tích xung quanh của hình lăng trụ là:

    5.4.x +8.x =20x +8x = 28x (m2)

    Mà diện tích xung quanh của hình lăng trụ bằng

    Do đó ta có: 28.x= 560

    Vậy chiều cao của hình lăng trụ trên là 20m

    Bài 5: Một hộp gỗ hình hộp chữ nhật không nắp có các kích thước đáy lần lượt là 50cm, 80cm và chiều cao là 40cm. Người ta sơn hết tất cả các mặt của thùng gỗ (biết bề dày sơn không đáng kể). Tính diện tích cần sơn.

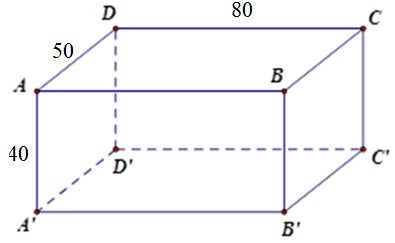
    Trắc nghiệm Diện tích xung quanh hình lăng trụ đứng có đáp án - Toán lớp 8 (ảnh 8)

    A. 10400 (cm2)

    B. 14400 (cm2)

    C. 4000 (cm2)

    D. 18400 (cm2)

    Đáp án: B

    Giải thích:

    Diện tích xung quanh bằng:

    2 (50+80).40=10400 (cm2)

    Diện tích một đáy bằng:

    50.80 = 4000 (cm2)

    Diện tích hình cần sơn là:

    10400 + 4000 = 14400 (cm2)

    Bài 6: Cho hình lăng trụ đứng ABC. A’B’C’ có đáy tam giác ABC vuông tại A, AB = 6 cm, AC = 8 cm, AA’ = 12 cm. Diện tích toàn phần của hình lăng trụ đó bằng

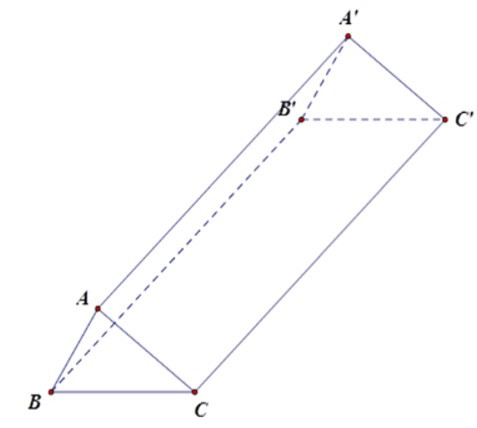
    Trắc nghiệm Diện tích xung quanh hình lăng trụ đứng có đáp án - Toán lớp 8 (ảnh 10)

    A. 288 cm2

    B. 360 cm2

    C. 456 cm2

    D. 336 cm2

    Đáp án: D

    Giải thích:

    Áp dụng định lý Pytago cho tam giác ABC ta được

    BC2 = AB2+AC2 

    = 62+82 = 10 cm

    Ta có chu vi đáy

    PABC = AB + AC + BC

    = 6 + 8 +10 = 24 cm

    Diện tích đáy SABC = AB.AC2 

    = 6.82 = 24 cm2

    Diện tích xung quanh của lăng trụ đứng

    Sxq = 24.12 = 288 cm2.

    Diện tích toàn phần Stp = 360 + 2.24 = 336 cm2.

    Bài 7: Cho hình lăng trụ đứng ABC.DEF, đáy là tam giác ABC có AB = 6 cm, BC = 8 cm, AC = 10 cm và chiều cao của lăng trụ là 12 cm. Diện tích toàn phần của hình lăng trụ đứng ABC.DEF là

    A. 240cm2

    B. 288cm2

    C. 480cm2

    D. 336cm2

    Đáp án: D

    Giải thích:

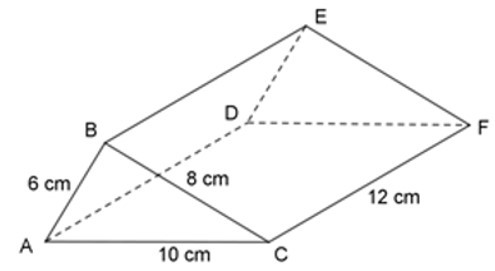
    Trắc nghiệm Diện tích xung quanh hình lăng trụ đứng có đáp án - Toán lớp 8 (ảnh 13)

    Ta có:

    AB2 + BC2 = 62 + 82 = 100

    AC2 = 102 = 100

    => AB2 + BC2 = AC2

    Áp dụng định lý đảo của định lý Pitago ta có tam giác ABC là tam giác vuông tại B

    Khi đó diện tích tam giác ABC:

    SΔABC=12AB.AC=12.6.8=24cm2

    Diện tích xung quanh của hình lăng trụ là:

    Diện tích toàn phần của hình lăng trụ là:

    Bài 8: Cho hình lăng trụ đứng tam giác ABC. A’B’C’ có chiều cao bằng 2 cm, có đáy là tam giác ABC vuông cân tại A và BAB'^ = 450. Tính diện tích toàn phần của hình lăng trụ đó.

    A. 8+42cm2

    B. 4 cm2

    C.12+42cm2

    D. 12 cm2

    Đáp án: C

    Giải thích:

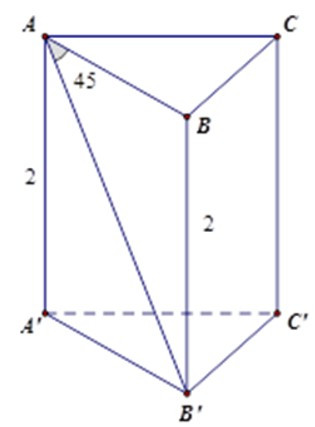
    Trắc nghiệm Diện tích xung quanh hình lăng trụ đứng có đáp án - Toán lớp 8 (ảnh 14)

    Tam giác vuông ABB’ có BAB'^ = 450 nên là tam giác vuông cân tại B nên AB = BB’ = 2 cm.

    Vì tam giác ABC vuông cân tại A nên AB = AC = 2cm

    ⇒BC=AB2+AC2=22cm

    Diện tích hai đáy là:

    2SΔABC=2.12AB.AC=2.12.2.2=4cm2

    Diện tích xung quanh bằng:

    2.2+2.2+2.22=8+42cm2

    Diện tích toàn phần của hình lăng trụ là:

    8+42+4=12+42cm2

    Bài 9: Cho hình lăng trụ ngũ giác đều ABCDE.A’B’C’D’E’, đáy là một ngũ giác đều có cạnh bằng 5cm, chiều cao của hình lăng trụ là 12cm. Tính diện tích xung quanh của hình lăng trụ ABCDE.A’B’C’D’E’.

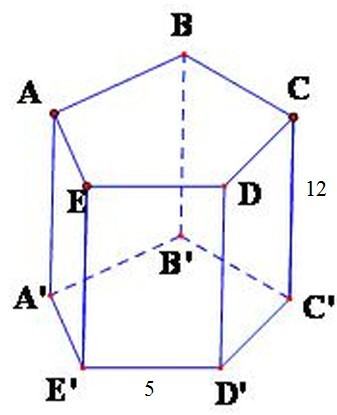
    Trắc nghiệm Diện tích xung quanh hình lăng trụ đứng có đáp án - Toán lớp 8 (ảnh 15)

    A. 240cm2

    B. 300cm2

    C. 250cm2

    D. 360cm2

    Đáp án: B

    Giải thích:

    Chu vi của đáy là: 5.5 = 25 cm

    Diện tích xung quanh của hình lăng trụ ABCDE.A’B’C’D’E’ là:

    Bài 10: Cho hình lăng trụ đứng ABC. A’B’C’ (hình vẽ) có BAC^ = 900, AB = 6 cm, AC = 8 cm,

    AA’ = 15 cm. Diện tích toàn phần của hình lăng trụ đứng bằng

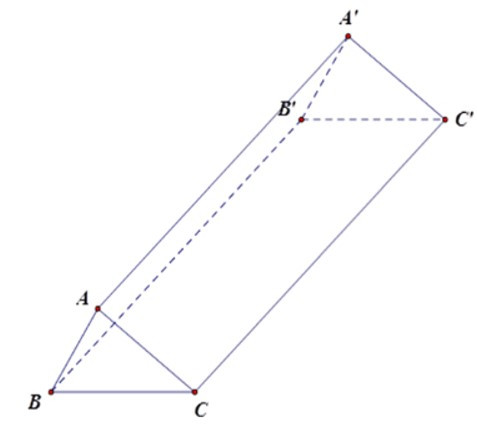
    Trắc nghiệm Diện tích xung quanh hình lăng trụ đứng có đáp án - Toán lớp 8 (ảnh 17)

    A. 258 cm2

    B. 360 cm2

    C. 456 cm2

    D. 408 cm2

    Đáp án: D

    Giải thích:

    Áp dụng định lý Pytago cho tam giác ABC ta được

    BC2 =AB2+AC2 

    = 62+82 = 10 cm

    Ta có chu vi đáy

    PABC = AB + AC + BC

    = 6 + 8 +10 = 24 cm

    Diện tích đáy SABC = AB.AC2 

    = 6.82 = 24 cm2

    Diện tích xung quanh của lăng trụ đứng

    Sxq = 24.15 = 360 cm2.

    Diện tích toàn phần

    Stp = 360 + 2.24 = 408 cm2.

    Xem thêm các bài tổng hợp lý thuyết Toán lớp 8 đầy đủ, chi tiết khác:

    Lý thuyết Thể tích của hình lăng trụ

    Lý thuyết Hình chóp đều và hình chóp cụt đều

    Lý thuyết Diện tích xung quanh của hình chóp đều

    Lý thuyết Thể tích của hình chóp đều

    Lý thuyết Ôn tập chương 4

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 2,192 25/02/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: