Lý thuyết Ôn tập chương 3 Tam giác đồng dạng (mới 2023 + Bài Tập) – Toán 8

Lý thuyết Toán 8 Ôn tập chương 3

Bài giảng Toán 8 Ôn tập chương 3

A. Lý thuyết

1. Định lí Ta- let trong tam giác

1.1. Tỉ số của hai đường thẳng

- Định nghĩa

Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.

Tỉ số của hai đoạn thẳng AB và CD được kí hiệu là $\frac{\mathrm{AB}}{\mathrm{CD}}$.

- Chú ý: Tỉ số của hai đoạn thẳng không phụ thuộc vào cách chọn đơn vị đo

Ví dụ 1.

- Cho AB = 10 cm; CD = 30 cm thì $\frac{\mathrm{AB}}{\mathrm{CD}}=\frac{10}{30}=\frac{1}{3}$

- Cho AB = 1 dm; CD = 3 dm thì $\frac{\mathrm{AB}}{\mathrm{CD}}=\frac{1}{3}$

1.2. Đoạn thẳng tỉ lệ

- Định nghĩa:

Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức $\frac{\mathrm{AB}}{\mathrm{CD}}=\frac{\mathrm{A}\text{'}\mathrm{B}\text{'}}{\mathrm{C}\text{'}\mathrm{D}\text{'}}$ hay $\frac{\mathrm{AB}}{\mathrm{A}\text{'}\mathrm{B}\text{'}}=\frac{\mathrm{CD}}{\mathrm{C}\text{'}\mathrm{D}\text{'}}$.

1.3. Định lý Ta – lét trong tam giác

- Định lý Ta – lét:

Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lai thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.

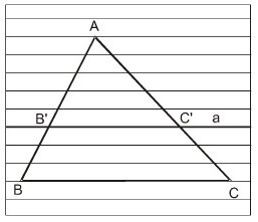
Tổng quát: $△\mathrm{ABC}, \mathrm{B}\text{'}\mathrm{C}\text{'}\parallel \mathrm{BC}; \mathrm{B}\text{'}\in \mathrm{AB}, \mathrm{C}\text{'}\in \mathrm{AC}$

Ta có: $\frac{\mathrm{AB}\text{'}}{\mathrm{AB}}=\frac{\mathrm{AC}\text{'}}{\mathrm{AC}}; \frac{\mathrm{AB}\text{'}}{\mathrm{BB}\text{'}}=\frac{\mathrm{AC}\text{'}}{\mathrm{C}\text{'}\mathrm{C}}; \frac{\mathrm{BB}\text{'}}{\mathrm{AB}}=\frac{\mathrm{CC}\text{'}}{\mathrm{AC}}$

Ví dụ 2. Tính độ dài cạnh AN trong hình vẽ sau, biết MN// BC

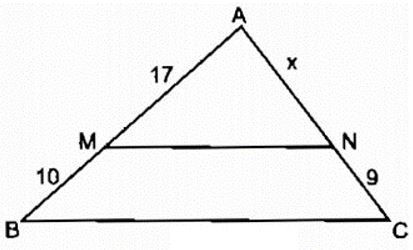
Lời giải:

Ta có MN// BC, áp dụng định lý Ta – lét ta có:

$\frac{\mathrm{AM}}{\mathrm{MB}}=\frac{\mathrm{AN}}{\mathrm{NC}}$ hay $\frac{17}{10}=\frac{\mathrm{x}}{9}$

$\Rightarrow \mathrm{x}=\frac{17.9}{10}=15,3$

Vậy AN = 15,3.

2. Định lí đảo và hệ quả của định lí Ta – lét

2.1. Định lý đảo

- Nếu một đường thẳng cắt hai cạnh một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

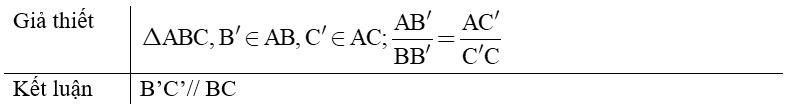
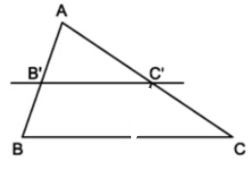
Ví dụ 3. Trong tam giác ABC có AB = 10cm; AC = 15cm. Lấy trên cạnh AB điểm B’, trên cạnh AC lấy điểm  C’ sao cho AB’ = 4cm; AC’ = 6cm. Chứng minh B’C’// BC.

Lời giải:

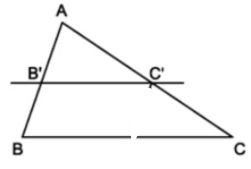
Ta có: B’B = AB – AB’ = 10 – 4 = 6cm,

Và CC’ = AC – AC’ = 15 – 6 = 9 cm

Ta có:

$$\begin{gathered} \frac{\mathrm{AB}\text{'}}{\mathrm{BB}\text{'}}=\frac{4}{6}=\frac{2}{3}; \frac{\mathrm{AC}\text{'}}{\mathrm{CC}\text{'}}=\frac{6}{9}=\frac{2}{3} \\ \Rightarrow \frac{\mathrm{AB}\text{'}}{\mathrm{BB}\text{'}}=\frac{\mathrm{AC}\text{'}}{\mathrm{CC}\text{'}} \end{gathered}$$

Theo định lí ta – lét đảo, suy ra: B’C’ // BC.

2.2. Hệ quả của định lý Ta – lét

- Nếu một đường thẳng cắt hai cạnh còn lại của một của một tam giác và song song với các cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh còn lại của tam giác đã cho.

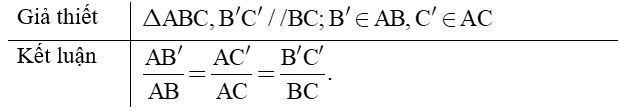
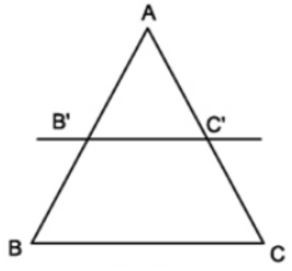
- Chú ý: Hệ quả trên vẫn đúng cho trường hợp đường thẳng song song với một cạnh và cắt phần kéo dài của hai cạnh còn lại.

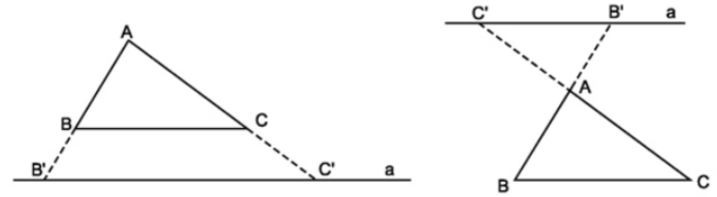
Ví dụ 4. Trong tam giác ABC có AB = 6cm và B’C’// BC . Lấy trên cạnh AB điểm B’, trên cạnh AC lấy điểm C’ sao cho AB’ = 4cm; AC’ = 3cm. Tính độ dài cạnh AC.

Lời giải:

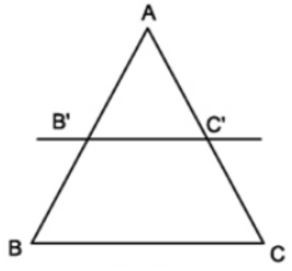
Áp dụng hệ quả trên ta có:

$\frac{\mathrm{AB}\text{'}}{\mathrm{AB}}=\frac{\mathrm{AC}\text{'}}{\mathrm{AC}}=\frac{\mathrm{B}\text{'}\mathrm{C}\text{'}}{\mathrm{BC}}$

Khi đó ta có:

$$\begin{gathered} \frac{\mathrm{AB}\text{'}}{\mathrm{AB}}=\frac{\mathrm{AC}\text{'}}{\mathrm{AC}}\iff \frac{4}{6}=\frac{3}{\mathrm{AC}} \\ \Rightarrow \mathrm{AC}=\frac{6.3}{4}=\frac{9}{2}\left(\mathrm{cm}\right) \end{gathered}$$

3. Tính chất đường phân giác của tam giác

3.1. Định lý

Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy.

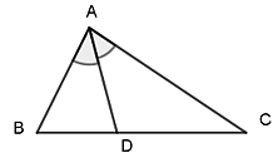
Ví dụ 5. Cho tam giác ABC có AD là đường phân giác của góc $\widehat{\mathrm{BAC}}$ sao cho DB = 4cm, AB = 6cm; AC = 8cm. Tính độ dài cạnh DC.

Lời giải:

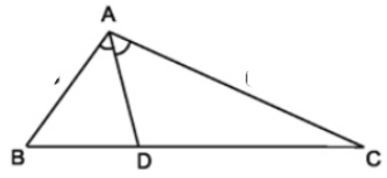
Áp dụng định lí trên ta có:

$\frac{\mathrm{DB}}{\mathrm{DC}}=\frac{\mathrm{AB}}{\mathrm{AC}}$

Hay $\frac{4}{\mathrm{DC}}=\frac{6}{8}\Rightarrow \mathrm{DC}=\frac{4.8}{6}=\frac{16}{3}\mathrm{cm}$

3.2. Chú ý

Định lí vẫn đúng với đường phân giác của góc ngoài của tam giác

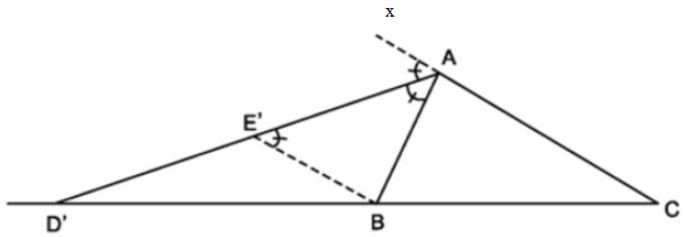
Nếu AE’ là phân giác của góc $\widehat{\mathrm{BAx}}$

Ta có: $\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{DB}\text{'}}{\mathrm{D}\text{'}\mathrm{C}}$.

4. Khái niệm tam giác đồng dạng

4.1.Tam giác đồng dạng

a) Định nghĩa

Tam giác A’B’C’ gọi là đồng dạng với tam giác ABC nếu:

$\hat{\mathrm{A}}=\widehat{\mathrm{A}\text{'}}; \hat{\mathrm{B}}=\widehat{\mathrm{B}\text{'}}; \hat{\mathrm{C}}=\widehat{\mathrm{C}\text{'}}$ và $\frac{\mathrm{A}\text{'}\mathrm{B}\text{'}}{\mathrm{AB}}=\frac{\mathrm{A}\text{'}\mathrm{C}\text{'}}{\mathrm{AC}}=\frac{\mathrm{B}\text{'}\mathrm{C}\text{'}}{\mathrm{BC}}$

Tam giác A’B’C’ đồng dạng với tam giác ABC được kí hiệu là ∆A’B’C’ $\infty$ ∆ABC.

Tỉ số các cạnh tương ứng $\frac{\mathrm{A}\text{'}\mathrm{B}\text{'}}{\mathrm{AB}}=\frac{\mathrm{A}\text{'}\mathrm{C}\text{'}}{\mathrm{AC}}=\frac{\mathrm{B}\text{'}\mathrm{C}\text{'}}{\mathrm{BC}}=\mathrm{k}$ được gọi là tỉ số đồng dạng

b) Tính chất

Các tính chất của hai tam giác đồng dạng:

Tính chất 1. Mỗi tam giác đồng dạng với chính nó.

Tính chất 2. Nếu  ∆ABC $\infty$ ∆ A’B’C’ thì ∆A’B’C’ $\infty$ ∆ ABC.

Tính chất 3. Nếu  ∆A’B’C’ $\infty$ ∆ A”B”C” và ∆A”B”C $\infty$ ∆ ABC thì ∆A’B’C’ $\infty$ ∆ ABC.

Ví dụ 6. Cho ∆A’B’C’∆ ABC như hình vẽ. Tính tỉ số đồng dạng ?

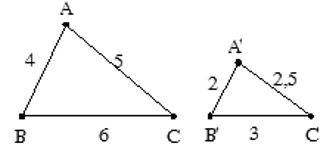
Lời giải:

Ta có ∆A’B’C’ $\infty$ ∆ ABC. Khi đó tỉ số đồng dạng là

$\frac{\mathrm{A}\text{'}\mathrm{B}\text{'}}{\mathrm{AB}}=\frac{\mathrm{A}\text{'}\mathrm{C}\text{'}}{\mathrm{AC}}=\frac{\mathrm{B}\text{'}\mathrm{C}\text{'}}{\mathrm{BC}}=\frac{2}{4}=\frac{2,5}{5}=\frac{3}{6}=\frac{1}{2}$

4.2. Định lý

Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.

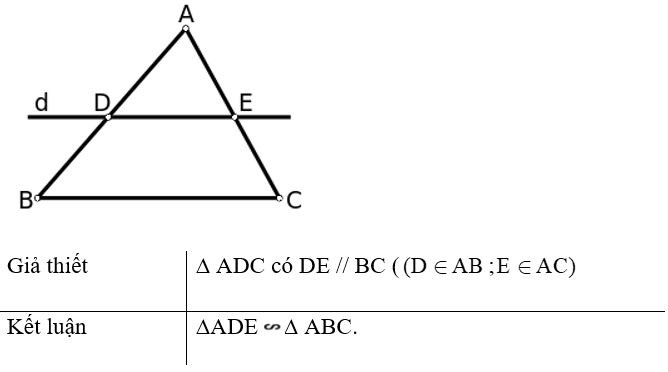
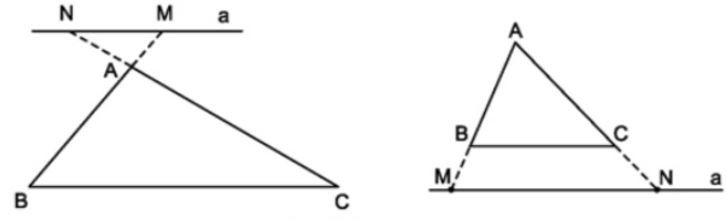
- Chú ý: Định lí cũng đúng cho trường hợp đường thẳng d cắt phần kéo dài của hai tam giác song song với cạnh còn lại.

5. Trường hợp đồng dạng thứ nhất.

5.1. Định lí

- Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.

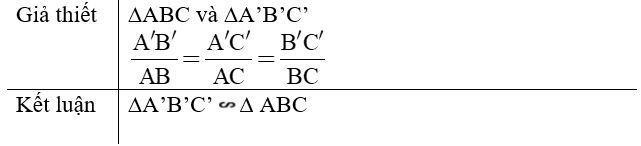
- Ví dụ 7. Cho ∆ABC và ∆A’B’C’ có độ dài các cạnh như hình vẽ.

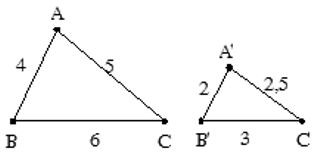
Ta có:

$\frac{\mathrm{A}\text{'}\mathrm{B}\text{'}}{\mathrm{AB}}=\frac{\mathrm{A}\text{'}\mathrm{C}\text{'}}{\mathrm{AC}}=\frac{\mathrm{B}\text{'}\mathrm{C}\text{'}}{\mathrm{BC}}$

$\left(\frac{2}{4}=\frac{2,5}{5}=\frac{3}{6}=\frac{1}{2}\right)$

Do đó, ∆A’B’C’ $\infty$ ∆ ABC.

6. Trường hợp đồng dạng thứ hai

6.1. Định lí.

- Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng

- Ví dụ 8. Cho tam giác ABC có AB = 15cm; AC = 20cm. Trên hai cạnh AB, AC lần lượt lấy 2 điểm E, D sao cho AD = 8cm; AE = 6cm.

Chứng minh ∆AED $\infty$ ∆ABC.

Lời giải:

            

Xét ∆AED và ∆ABC có:

$\left\{\begin{array}{l}\hat{\mathrm{A}} \mathrm{chung}\\ \frac{\mathrm{AE}}{\mathrm{AB}}=\frac{\mathrm{AD}}{\mathrm{AC}}\left(\frac{6}{15}=\frac{8}{20}=\frac{2}{5}\right)\end{array}\right.$

Suy ra: ∆AED $\infty$ ∆ABC.

7. Trường hợp đồng dạng thứ ba

7.1. Định lí

- Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.

- Ví dụ 9. Cho tam giác ABC và các đường cao BH, CK. Chứng minh ∆ABH $\infty$ ∆ ACK.  

Lời giải:

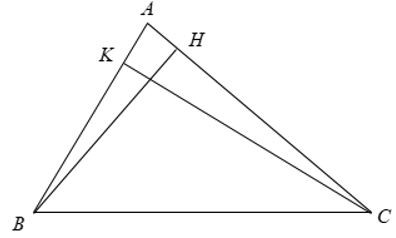
Xét ∆ABH và ∆ACK có:

$\left\{\begin{array}{l}\hat{\mathrm{A}} \mathrm{chung}\\ \widehat{\mathrm{AHB}}=\widehat{\mathrm{AKC}}=90°\end{array}\right.$

Suy ra: ∆ABH $\infty$ ∆ACK.

8. Các trường hợp đồng dạng của tam giác vuông

8.1. Áp dụng các trường hợp đồng dạng của tam giác vào tam giác vuông

Hai tam giác vuông đồng dạng với nhau nếu:

+ Tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia.

+ Tam giác vuông này có hai cạnh góc vuông tỉ lệ với hai cạnh góc vuông của tam giác vuông kia.

8.2. Dấu hiệu đặc biệt nhận biết hai tam vuông đồng dạng

- Định lý 1: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

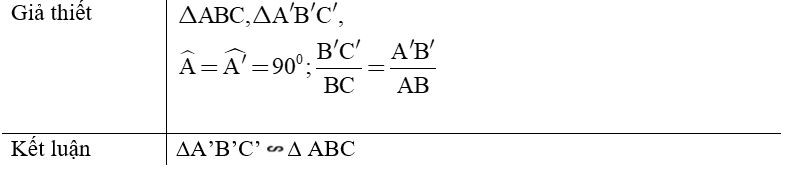
8.3. Tỉ số hai đường cao, tỉ số diện tích của hai tam giác đồng dạng

- Định lý 2: Tỉ số hai đường cao tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.

Cho hai tam giác ABC và A’B’C’ với tỉ số đồng dạng là $\mathrm{k}=\frac{\mathrm{A}\text{'}\mathrm{B}\text{'}}{\mathrm{AB}}$, hai đường cao tương ứng là AH và A’H’.

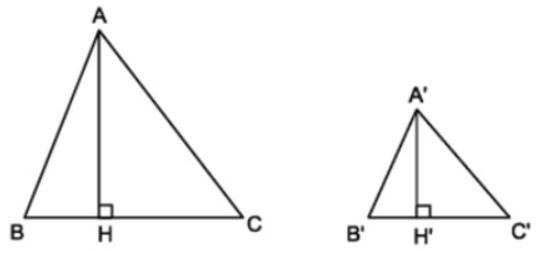
Khi đó, ta có tỉ số hai đường cao là: $\frac{{\mathrm{h}}_{∆\mathrm{A}\text{'}\mathrm{B}\text{'}\mathrm{C}\text{'}}}{{\mathrm{h}}_{∆\mathrm{ABC}}}=\mathrm{k}$.

- Định lý 3: Tỉ số diện tích hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng.

Ví dụ 10. Cho tam giác ABC đồng dạng với tam giác MNP theo tỉ số $\mathrm{k}=\frac{2}{3}$. Biết đường cao xuất phát từ A của tam giác ABC là AH = 12cm. Tính đường cao xuất phát từ M của tam giác MNP?

Lời giải:

Gọi đường cao xuất phát từ M của tam giác MNP là MK.

Vì tam giác ABC đồng dạng với tam giác MNP theo tỉ số $\mathrm{k}=\frac{2}{3}$ nên

$\frac{\mathrm{AH}}{\mathrm{MK}}=\mathrm{k}\Rightarrow \frac{12}{\mathrm{MK}}=\frac{2}{3}\Rightarrow \mathrm{MK}=\frac{12.3}{2}=18$

Vậy MK = 18 cm.

B. Bài tập tự luyện

Bài 1. Viết tỉ số của các cặp đoạn thẳng có độ dài như sau:

a) AB = 6 cm; CD = 10 cm.

b) AB = 2dm; MN = 4cm.

c) MN = 12 cm; PQ = 2dm

Lời giải:

Tỉ số của các cặp đoạn thẳng đã cho là:

a) $\frac{\mathrm{AB}}{\mathrm{CD}}=\frac{6}{10}=\frac{3}{5}$

b) Đổi AB = 2 dm = 20 cm

$\frac{\mathrm{AB}}{\mathrm{MN}}=\frac{20}{4}=5$

c) Đổi PQ = 2dm = 20 cm

$\frac{\mathrm{MN}}{\mathrm{PQ}}=\frac{12}{20}=0,6$

Bài 2. Tìm độ dài x cho hình vẽ sau biết MN// BC

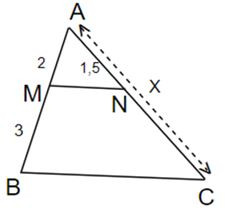
Lời giải:

Ta có: MN// BC. Áp dụng định lí Ta – lét ta có:

$$\begin{gathered} \frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AC}}\iff \frac{2}{5}=\frac{1,5}{\mathrm{x}} \\ \Rightarrow \mathrm{x}=\frac{5.1,5}{2}=3,75 \end{gathered}$$

Vậy x = 3,75.

Bài 3. Cho các đoạn thẳng AB = 4 cm; CD = 8cm; MN = 20cm; PQ = x cm. Tìm x để  AB và CD tỉ lệ với MN và PQ?

Lời giải:

Để AB và CD tỉ lệ với MN và PQ thì:

$$\begin{gathered} \frac{\mathrm{AB}}{\mathrm{CD}}=\frac{\mathrm{MN}}{\mathrm{PQ}}\iff \frac{4}{8}=\frac{20}{\mathrm{x}} \\ \iff \mathrm{x}=\frac{8.20}{4}=40\mathrm{cm} \end{gathered}$$

Bài 4. Cho đoạn thẳng AB = 15cm. Trên đoạn thẳng AB lấy điểm C sao cho $\frac{\mathrm{CA}}{\mathrm{CB}}=\frac{3}{2}$. Tính độ dài đoạn CB.

Lời giải:

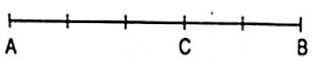
Từ giả thiết

$\frac{\mathrm{CA}}{\mathrm{CB}}=\frac{3}{2}\Rightarrow \frac{\mathrm{CA}}{3}=\frac{\mathrm{CB}}{2}$

Đặt $\frac{\mathrm{CA}}{3}=\frac{\mathrm{CB}}{2}=\mathrm{t} \left(\mathrm{t}>0\right)$

$\Rightarrow \left\{\begin{array}{l}\mathrm{CA}=3\mathrm{t}\\ \mathrm{CB}=2\mathrm{t}\end{array}\right.$

Ta có: AB = AC + CB

Thay số: 15 = 3t + 2t

Do đó, 15 = 5t nên t = 3.

Khi đó; CB = 2t = 2.3 = 6 cm.

Vậy CB = 6cm.

Bài 5. Tính x trong hình vẽ sau, biết FG// HT

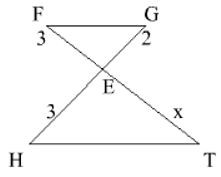
Lời giải:

Áp dụng hệ quả của định lí Ta – lét với FG// HT ta có:

$\frac{\mathrm{EF}}{\mathrm{ET}}=\frac{\mathrm{EG}}{\mathrm{HE}}\iff \mathrm{ET}=\frac{\mathrm{EF}.\mathrm{HE}}{\mathrm{EG}}=\frac{3.3}{2}=4,5$

Vậy x = 4,5.

Bài 6. Tính độ dài x, y trong các hình sau biết DE // BC

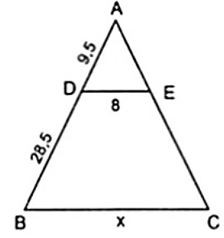
Lời giải:

a) Áp dụng hệ quả của định lí Ta – lét ta có:

$\frac{\mathrm{BC}}{\mathrm{DE}}=\frac{\mathrm{AB}}{\mathrm{AD}}$ hay $\frac{\mathrm{x}}{8}=\frac{28,5+9,5}{9,5}=\frac{38}{9,5}$

$\iff \mathrm{x}=\frac{8.38}{9,5}=32$

b) Ta có: A’B’// AB vì cùng vuông góc AA’.

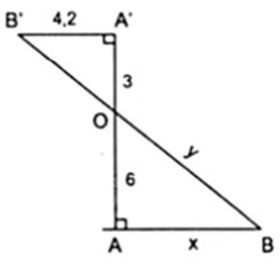
Áp dụng hệ quả của định lí Ta – lét ta có:

$\mathrm{A}\text{'}\mathrm{B}\text{'}\parallel \mathrm{AB}\Rightarrow \frac{\mathrm{AB}}{\mathrm{A}\text{'}\mathrm{B}\text{'}}=\frac{\mathrm{AO}}{\mathrm{A}\text{'}\mathrm{O}\text{'}}$

hay $\frac{\mathrm{x}}{4,2}=\frac{6}{3}\iff \mathrm{x}=8,4$

Áp dụng định lí Py – ta – go với tam giác OAB ta có:

${\mathrm{OB}}^2={\mathrm{AB}}^2+{\mathrm{OA}}^2\Rightarrow \mathrm{y}=\sqrt{8,4^2+6^2}\approx 10,32$

Vậy x = 8,4 và $\mathrm{y}\approx 10,32$.

Bài 7. Cho tam giác ABC, một đường thẳng d cắt 2 cạnh  AB và AC tại M và N  sao cho AM =  4cm, MB = 5cm, AN = 6 cm và  AC = 13,5cm; BC = 12 cm. Tính MN?

Lời giải:

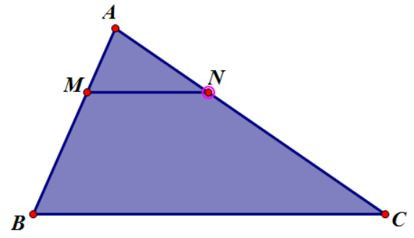
Do N nằm giữa A và C nên:

NC = AC-  AN =  13,5 -  6 = 7,5cm

Ta có: $\frac{\mathrm{AM}}{\mathrm{MB}}=\frac{\mathrm{AN}}{\mathrm{NC}} \left(\frac{4}{5}=\frac{6}{7,5}\right)$

Suy ra: MN // BC (định lí Ta let đảo)

Theo hệ quả định lí ta let ta có;

$\frac{\mathrm{AN}}{\mathrm{AC}}=\frac{\mathrm{MN}}{\mathrm{BC}}\Rightarrow \mathrm{MN}=\frac{\mathrm{AN}.\mathrm{BC}}{\mathrm{AC}}=\frac{6.12}{13,5}=\frac{16}{3}\mathrm{cm}$

Vậy MN = $\frac{16}{3}\mathrm{cm}$.

Bài 8. Cho tam giác ABC, đường thẳng d song song với BC cắt 2 cạnh  AB  và AC lần lượt tại M và N.  Biết rằng $\frac{\mathrm{AM}}{\mathrm{MB}}=\frac{1}{2}$. Tỉnh tỉ số chu vi tam giác AMN và ABC ?

Lời giải:

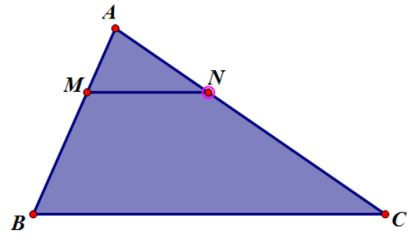
Ta có: $\frac{\mathrm{AM}}{\mathrm{MB}}=\frac{1}{2}\Rightarrow \frac{\mathrm{AM}}{\mathrm{MB}+\mathrm{AM}}=\frac{1}{2+1}\Rightarrow \frac{\mathrm{AM}}{\mathrm{AB}}=\frac{1}{3}$

Vì MN// BC nên theo hệ quả định lí Ta let ta có:

$\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AC}}=\frac{\mathrm{MN}}{\mathrm{BC}}=\frac{1}{3}$

Áp dụng tính chất của dãy tỉ số bằng nhau ta có: 

$\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AC}}=\frac{\mathrm{MN}}{\mathrm{BC}}=\frac{\mathrm{AM}+\mathrm{AN}+\mathrm{MN}}{\mathrm{AB}+\mathrm{AC}+\mathrm{BC}}=\frac{1}{3}$

Do đó, tỉ số chu vi tam giác AMN  và ABC là $\frac{1}{3}$.

Bài 9. Cho tam giác ABC vuông tại A có AB = 6cm; BC = 10cm, AD là đường phân giác của tam giác. Tính BD; CD

Lời giải:

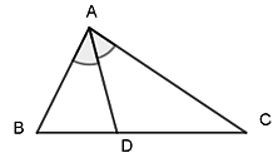
Áp dụng định lý Py – ta – go vào tam giác vuông ABC ta có:

AC² = BC² – AB²

nên $\mathrm{AC}=\sqrt{{\mathrm{BC}}^2-{\mathrm{AB}}^2}=\sqrt{{10}^2-6^2}=8\left(\mathrm{cm}\right)$

Tam  giác ABC có AD là đường phân giác của góc $\widehat{\mathrm{BAC}}$

Ta có: $\frac{\mathrm{DB}}{\mathrm{DC}}=\frac{\mathrm{AB}}{\mathrm{AC}}$.

Khi đó ta có: $\frac{\mathrm{DB}}{\mathrm{DC}}=\frac{\mathrm{AB}}{\mathrm{AC}}\Rightarrow \frac{\mathrm{DB}}{\mathrm{DB}+\mathrm{DC}}=\frac{\mathrm{AB}}{\mathrm{AB}+\mathrm{AC}}$ ( tính chất tỉ lệ thức)

Hay

$$\begin{gathered} \frac{\mathrm{DB}}{10}=\frac{6}{6+8}\Rightarrow \mathrm{DB}=\frac{30}{7}\mathrm{cm}; \\ \mathrm{DC}=\mathrm{BC}-\mathrm{DB}=\frac{40}{7}\mathrm{cm} \end{gathered}$$

Vậy $\mathrm{DB}=\frac{30}{7}\mathrm{cm}$ và $\mathrm{DC}=\frac{40}{7}\mathrm{cm}$

Bài 10. Cho tam giác ABC vuông tại A, đường phân giác BD. Tính AB, BC biết AD = 4 cm và DC = 5cm.

Lời giải:

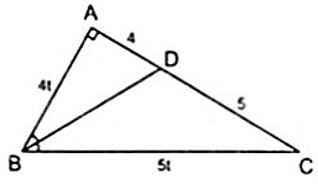
Áp dụng tính chất đường phân giác BD của tam giác ABC, ta có:

$\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{DA}}{\mathrm{DC}}=\frac{4}{5}\Rightarrow \frac{\mathrm{AB}}{4}=\frac{\mathrm{BC}}{5}$

Đặt $\frac{\mathrm{AB}}{4}=\frac{\mathrm{BC}}{5}$= t ( t > 0)

$\Rightarrow \left\{\begin{array}{l}\mathrm{AB}=4\mathrm{t}\\ \mathrm{BC}=5\mathrm{t}\end{array}\right.$

Áp dụng định lý Py – ta – go vào tam giác ABC ta có:

BC² = AC² + AB² hay ( 5t)²  = 9²  + (4t)²

9t²  = 81.t² = 9 nên t = 3  ( vì t > 0)

Khi đó: AB = 4.3 = 12 cm;  BC = 5.3 = 15 cm.

Vậy AB = 12cm, BC = 15cm.

Bài 11. Cho tam giác ABC, các đường phân giác BD và CE. Biết $\frac{\mathrm{AD}}{\mathrm{DC}}=\frac{2}{3}$, $\frac{\mathrm{EA}}{\mathrm{EB}}=\frac{5}{6}$. Tính các cạnh của tam giác ABC, biết chu vi của tam giác là 45cm.

Lời giải:

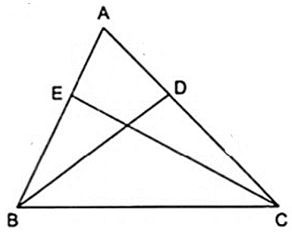
Áp dụng tính chất của các đường phân giác BD và CE của tam giác ABC ta được:

$$\begin{gathered} \frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{AD}}{\mathrm{DC}}=\frac{2}{3}=\frac{4}{6} \\ \Rightarrow \frac{\mathrm{AB}}{4}=\frac{\mathrm{BC}}{6}=\mathrm{t}\Rightarrow \left\{\begin{array}{l}\mathrm{AB}=4\mathrm{t}\\ \mathrm{BC}=6\mathrm{t}\end{array}\right. \\ \frac{\mathrm{AC}}{\mathrm{BC}}=\frac{\mathrm{AE}}{\mathrm{EB}}=\frac{5}{6} \\ \Rightarrow \frac{\mathrm{AC}}{5}=\frac{\mathrm{BC}}{6}=\mathrm{t}\Rightarrow \left\{\begin{array}{l}\mathrm{AC}=5\mathrm{t}\\ \mathrm{BC}=6\mathrm{t}\end{array}\right. \end{gathered}$$

Theo giả thiết ta có, chu vi tam giác ABC là 45 nên:

AB + BC + AC = 15t = 45 nên t = 3.

Vậy AB = 12 cm; BC = 18cm; AC = 15cm .

Bài 12. Cho tam giác ABC có đường trung tuyến AM  và đường phân giác AD của góc $\widehat{\mathrm{BAC}}$. Biết AB = 12 cm;  AC = 8cm  và BC = 15cm. Tính tỉ số $\frac{\mathrm{BM}}{\mathrm{BD}}$.

Lời giải:

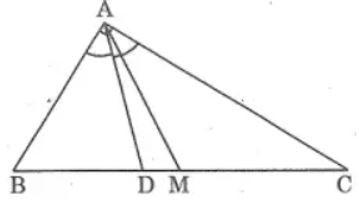
Do M là  trung điểm của BC nên:

$\mathrm{BM}=\mathrm{MC}=\frac{1}{2}\mathrm{BC}=\frac{1}{2}.15=7,5\mathrm{cm}$

Theo tính chất tia phân giác của góc ta có: $\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{DB}}{\mathrm{DC}}$

Suy ra: $\frac{\mathrm{AB}}{\mathrm{DB}}=\frac{\mathrm{AC}}{\mathrm{DC}}$

Theo tính chất của dãy tỉ số bằng  nhau ta có:

$\frac{\mathrm{AB}}{\mathrm{DB}}=\frac{\mathrm{AC}}{\mathrm{DC}}=\frac{\mathrm{AB}+\mathrm{AC}}{\mathrm{DB}+\mathrm{DC}}=\frac{12+8}{15}=\frac{4}{3}$

Suy ra: 

$\frac{\mathrm{AB}}{\mathrm{BD}}=\frac{4}{3}\Rightarrow \mathrm{BD}=\frac{3.\mathrm{AB}}{4}=\frac{3.12}{4}=9\mathrm{cm}$

Do đó: $\frac{\mathrm{BM}}{\mathrm{BD}}=\frac{7,5}{9}=\frac{5}{6}$

Vậy $\frac{\mathrm{BM}}{\mathrm{BD}}=\frac{5}{6}$

Bài 13. Cho ∆A’B’C’ $\infty$ ∆ ABC có $\frac{\mathrm{AB}}{\mathrm{A}\text{'}\mathrm{B}\text{'}}=\frac{3}{7}$. Biết hiệu số chu vi của ∆A’B’C’ và ∆ABC là 40cm. Tính chu vi của hai tam giác ABC và A’B’C’

Lời giải:

Ta có: ∆A’B’C’∆ ABC nên:

$\frac{\mathrm{AB}}{\mathrm{A}\text{'}\mathrm{B}\text{'}}=\frac{\mathrm{AC}}{\mathrm{A}\text{'}\mathrm{C}\text{'}}=\frac{\mathrm{BC}}{\mathrm{B}\text{'}\mathrm{C}\text{'}}=\frac{3}{7}$

Theo tính chất của dãy tỉ số bằng nhau ta có:

$\frac{\mathrm{AB}}{\mathrm{A}\text{'}\mathrm{B}\text{'}}=\frac{\mathrm{AC}}{\mathrm{A}\text{'}\mathrm{C}\text{'}}=\frac{\mathrm{BC}}{\mathrm{B}\text{'}\mathrm{C}\text{'}}=\frac{3}{7}=\frac{\mathrm{AB}+\mathrm{AC}+\mathrm{BC}}{\mathrm{A}\text{'}\mathrm{B}\text{'}+\mathrm{A}\text{'}\mathrm{C}\text{'}+\mathrm{B}\text{'}\mathrm{C}\text{'}}$

Khi đó $\frac{{\mathrm{P}}_{\mathrm{ABC}}}{{\mathrm{P}}_{\mathrm{A}\text{'}\mathrm{B}\text{'}\mathrm{C}\text{'}}}=\frac{3}{7}\Rightarrow {\mathrm{P}}_{\mathrm{ABC}}=\frac{3}{7}{\mathrm{P}}_{\mathrm{A}\text{'}\mathrm{B}\text{'}\mathrm{C}}$

Mà P_A’B’C’ – P_ABC = 40cm

Nên: ${\mathrm{P}}_{\mathrm{A}\text{'}\mathrm{B}\text{'}\mathrm{C}\text{'}}-\frac{3}{7}{\mathrm{P}}_{\mathrm{A}\text{'}\mathrm{B}\text{'}\mathrm{C}\text{'}}=40\iff \frac{4}{7}{\mathrm{P}}_{\mathrm{A}\text{'}\mathrm{B}\text{'}\mathrm{C}\text{'}}=40$

Nên P_A’B’C’ = 70cm và P_ABC = 30 cm.

Vậy chu vi của ∆ ABC là 30cm, chu vi của ∆A’B’C’ là 70cm.

Bài 14. Cho ∆ MNP có MN = 4cm; NP = 6cm; PQ = 8cm. Tam giác M’N’P’ đồng dạng với tam giác MNP có độ dài cạnh lớn nhất là 16 cm. Tính độ dài các cạnh còn lại của ∆M’N’P’?

Lời giải:

Tam giác MNP có cạnh PQ dài nhất.

Mà ∆M’N’P’ $\infty$ ∆ MNP nên cạnh P’Q’ là cạnh dài nhất trong tam giác M’N’P’

Ta có: ∆M’N’P’ $\infty$ ∆ MNP

$$\begin{gathered} \Rightarrow \frac{\mathrm{M}\text{'}\mathrm{N}\text{'}}{\mathrm{MN}}=\frac{\mathrm{N}\text{'}\mathrm{P}\text{'}}{\mathrm{NP}}=\frac{\mathrm{M}\text{'}\mathrm{P}\text{'}}{\mathrm{MP}} \\ \Rightarrow \frac{\mathrm{M}\text{'}\mathrm{N}\text{'}}{4}=\frac{\mathrm{N}\text{'}\mathrm{P}\text{'}}{6}=\frac{16}{8}=2 \end{gathered}$$

Suy ra: M’N’ = 2.4 = 8 cm

N’P’ = 6.2 = 12 cm.

Bài 15. Cho ∆ ABC ∆ MNP có tỉ số đồng dạng là $\mathrm{k}=\frac{2}{7}$, chu vi của ∆ABC  bằng 12cm. Chu vi của ∆MNP là?

Lời giải:
Ta có: ∆ ABC $\infty$ ∆MNP nên:

$\frac{\mathrm{AB}}{\mathrm{MN}}=\frac{\mathrm{BC}}{\mathrm{NP}}=\frac{\mathrm{AC}}{\mathrm{MP}}=\frac{2}{7}$

Theo tính chất của dãy tỉ số bằng nhau ta có:

$\frac{\mathrm{AB}}{\mathrm{MN}}=\frac{\mathrm{BC}}{\mathrm{NP}}=\frac{\mathrm{AC}}{\mathrm{MP}}=\frac{\mathrm{AB}+\mathrm{BC}+\mathrm{AC}}{\mathrm{MN}+\mathrm{NP}+\mathrm{MP}}=\frac{{\mathrm{P}}_{\mathrm{ABC}}}{{\mathrm{P}}_{\mathrm{MNP}}}=\frac{2}{7}$

Mà P_ABC = 12cm nên P_MNP = 42 cm.

Bài 16. Cho các tam giác có độ dài các cạnh lần lượt như sau. Hỏi hai tam giác có đồng dạng không?

a) 3cm; 4 cm; 5cm và 6cm; 8cm; 10cm

b) 3cm; 5cm; 7cm và 6cm; 12cm; 14cm

c) 4cm; 10cm; 8cm và 7cm; 12cm; 14cm

Lời giải:

a) Ta có:

$\frac{3}{6}=\frac{4}{8}=\frac{5}{10}=\left(=\frac{1}{2}\right)$ nên hai tam giác này có đồng dạng với nhau.

b) Ta có:

$\frac{3}{6}=\frac{7}{14}\ne \frac{5}{12}$ nên hai tam giác này không đồng dạng với nhau.

c) Sắp xếp độ dài các cạnh của hai tam giác theo thứ tự tăng dần:

4cm; 8cm; 10 cm và 7cm; 12cm; 14cm

Ta có: $\frac{4}{7}\ne \frac{8}{12}\ne \frac{10}{14}$ nên hai tam giác này không đồng dạng với nhau.

Bài 17. Tứ giác ABCD có AB = 2cm; BC = 6cm; CD = 8cm; DA = 3cm và BD = 4 cm.

Chứng minh rằng:

a) ∆BAD $\infty$ ∆ DBC.

b) ABCD là hình thang

Lời giải:

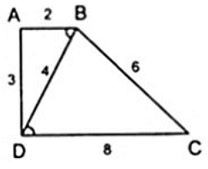
a) Ta có: $\frac{\mathrm{BA}}{\mathrm{BD}}=\frac{\mathrm{AD}}{\mathrm{BC}}=\frac{\mathrm{BD}}{\mathrm{CD}}=\frac{1}{2}$

Suy ra: ∆BAD $\infty$ ∆DBC (c.c.c)

b) Theo a ta có: ∆BAD $\infty$ ∆DBC

$\Rightarrow \widehat{\mathrm{ABD}}=\widehat{\mathrm{BDC}}$ nên AB // CD.

Suy ra, ABCD là hình thang.

Bài 18. Cho tam giác ABC có độ dài các cạnh AB = 4cm; BC = 7cm và AC = 8cm. Biết tam giác A’B’C’ đồng dạng với tam giác ABC và chu vi tam giác A’B’C’ là 38cm. Tính độ dài các cạnh của tam giác A’B’C’.

Lời giải:

Chu vi của tam giác ABC là: P_ABC = AB + BC + CA = 19 cm

Vì ∆A’B’C’ $\infty$ ∆ABC nên ta có:

$\frac{\mathrm{A}\text{'}\mathrm{B}\text{'}}{\mathrm{AB}}=\frac{\mathrm{B}\text{'}\mathrm{C}\text{'}}{\mathrm{BC}}=\frac{\mathrm{A}\text{'}\mathrm{C}\text{'}}{\mathrm{AC}}$

Theo tính chất của dãy tỉ số bằng nhau ta có:

$\frac{\mathrm{A}\text{'}\mathrm{B}\text{'}}{\mathrm{AB}}=\frac{\mathrm{B}\text{'}\mathrm{C}\text{'}}{\mathrm{BC}}=\frac{\mathrm{A}\text{'}\mathrm{C}\text{'}}{\mathrm{AC}}=\frac{\mathrm{A}\text{'}\mathrm{B}\text{'}+\mathrm{B}\text{'}\mathrm{C}\text{'}+\mathrm{C}\text{'}\mathrm{A}\text{'}}{\mathrm{AB}+\mathrm{BC}+\mathrm{CA}}=\frac{{\mathrm{P}}_{\mathrm{A}\text{'}\mathrm{B}\text{'}\mathrm{C}\text{'}}}{{\mathrm{P}}_{\mathrm{ABC}}}=\frac{38}{19}=2$

Suy ra: A’B’ = 2AB = 2.4 = 8cm

B’C’ = 2BC = 2.7 = 14 cm

Và A’C’ = 2AC = 2.8 = 16cm

Bài 19. Cho góc $\widehat{\mathrm{xOy}}\ne 180°$. Trên tia Ox lấy 2 điểm A và C sao cho OA = 4cm; OC = 10cm. Trên tia Oy lấy hai điểm B và D sao cho OB = 5cm; OD = 8cm

Chứng minh ∆OBC $\infty$ ∆OAD.

Lời giải:

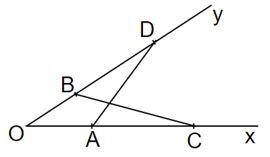
Xét ∆OBC và ∆ OAD có:

$\hat{\mathrm{O}}$ chung.

$\frac{\mathrm{OB}}{\mathrm{OA}}=\frac{\mathrm{OC}}{\mathrm{OD}}\left(\frac{5}{4}=\frac{10}{8}\right)$

Suy ra: ∆OBC $\infty$ ∆OAD (đpcm).

Bài 20. Cho tam giác ABC có AC = 12cm; BC = 8cm. Trên cạnh  AC lấy điểm E sao cho AE = 7cm. Trên cạnh BC lấy điểm D sao cho DC = 4,5. Chứng minh; $\widehat{\mathrm{EDC}}=\widehat{\mathrm{BAC}}$.

Lời giải:

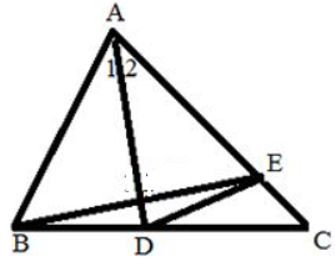
Ta có: CE = AC – AE = 10 – 7 = 3cm

Xét  ∆CED và ∆ CBA có:

$\hat{\mathrm{C}}$ chung.

$\frac{\mathrm{CE}}{\mathrm{CB}}=\frac{\mathrm{CD}}{\mathrm{CA}}\left(\frac{3}{8}=\frac{4,5}{12}\right)$

Suy ra: ∆CED $\infty$ ∆CBA (c.g.c)

Do đó: $\widehat{\mathrm{EDC}}=\widehat{\mathrm{BAC}}$ (2 góc tương ứng) (đpcm).

Bài 21. Chỉ ra các tam giác đồng dạng với nhau trong hình vẽ sau?

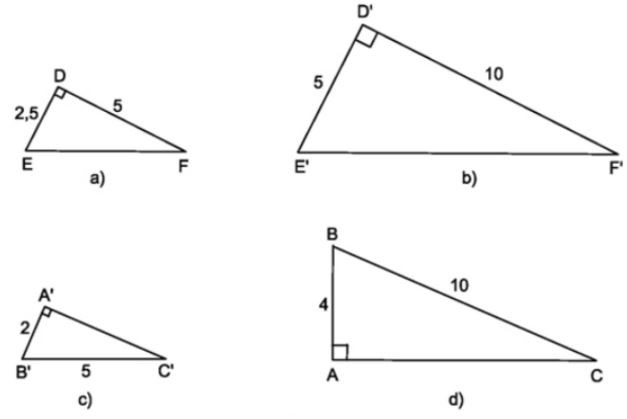
Lời giải:

+ Xét ∆DEF và ∆ D’E’F’ có:

$$\begin{gathered} \hat{\mathrm{D}}=\widehat{\mathrm{D}\text{'}}=90° \\ \frac{\mathrm{DE}}{\mathrm{D}\text{'}\mathrm{E}\text{'}}=\frac{\mathrm{DF}}{\mathrm{D}\text{'}\mathrm{F}\text{'}}=\frac{1}{2} \end{gathered}$$

Suy ra: ∆DEF $\infty$ ∆D’E’F’.

+ Áp dụng định lí py tago ta có:

$$\begin{gathered} \mathrm{A}\text{'}\mathrm{C}\text{'}=\sqrt{\mathrm{B}\text{'}\mathrm{C}{\text{'}}^2-\mathrm{A}\text{'}\mathrm{B}{\text{'}}^2}=\sqrt{21} \\ \mathrm{AC}=\sqrt{{\mathrm{BC}}^2-{\mathrm{AB}}^2}=\sqrt{84}=2\sqrt{21} \end{gathered}$$

Xét ∆ABC và ∆ A’B’C’ có:

$$\begin{gathered} \hat{\mathrm{A}}=\widehat{\mathrm{A}\text{'}}=90° \\ \frac{\mathrm{AB}}{\mathrm{A}\text{'}\mathrm{B}\text{'}}=\frac{\mathrm{AC}}{\mathrm{A}\text{'}\mathrm{C}\text{'}}=2 \end{gathered}$$

Suy ra: ∆ABC $\infty$ ∆A’B’C’.

Bài 22. Cho hình bên, ABCD là hình thang (AB// CD) có AB = 12 cm ; CD = 27cm và $\widehat{\mathrm{DAB}}=\widehat{\mathrm{DBC}}$. Tính độ dài đoạn BD gần nhất bằng bao nhiêu?

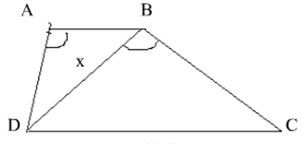
Lời giải:

Xét ∆ABD và ∆BDC có:

$\left\{\begin{array}{l}\widehat{\mathrm{BAD}}=\widehat{\mathrm{DBC}}\\ \widehat{\mathrm{ABD}}=\widehat{\mathrm{BDC}}\end{array}\right.$

Suy ra: ∆ABD $\infty$ ∆BDC (g.g). 

$\Rightarrow \frac{\mathrm{AB}}{\mathrm{BD}}=\frac{\mathrm{AD}}{\mathrm{BC}}=\frac{\mathrm{BD}}{\mathrm{DC}}$ hay

$\frac{12}{\mathrm{x}}=\frac{\mathrm{x}}{27}\Rightarrow {\mathrm{x}}^2=12.27=324$

$\iff \mathrm{x}=18$

Bài 23. Cho góc xOy khác góc bẹt. Trên tia Ox lấy 2 điểm A và B sao cho:  OA = 5cm; OB = 16cm. Trên tia Oy, lấy hai điểm C và D sao cho OC = 8cm; OD =10cm.

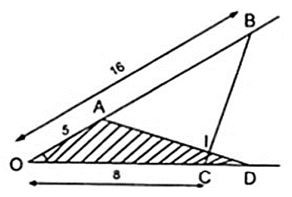
a) Chứng minh ∆OCB $\infty$ ∆OAD.

b) Gọi I là giao điểm của các cạnh AD và BC. Chứng minh rằng ∆IBA ∆ IDC

Lời giải:

a) Xét ∆OCB và ∆ OAD có

$\left\{\begin{array}{l}\hat{\mathrm{O}} \mathrm{chung}\\ \frac{\mathrm{OC}}{\mathrm{OA}}=\frac{\mathrm{OB}}{\mathrm{OD}}\left(\frac{8}{5}=\frac{16}{10}\right)\end{array}\right.$

Suy ra: ∆OCB $\infty$ ∆OAD (c.g.c)

b)  Theo a ta có: ∆OCB $\infty$ ∆OAD

$\Rightarrow \widehat{\mathrm{ADO}}=\widehat{\mathrm{CBO}}$ hay $\widehat{\mathrm{IDC}}=\widehat{\mathrm{IBA}}$ (1)

Mà $\widehat{\mathrm{CID}}=\widehat{\mathrm{AIB}}$ (vì đối đỉnh)  (2)

Từ (1) và (2) suy ra: ∆IBA $\infty$ ∆IDC (g.g)

Bài 24. Tìm x , y trong hình vẽ sau:

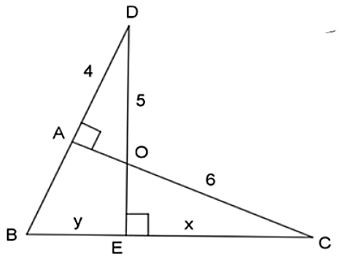
Lời giải:

Xét ∆OAD và ∆OEC có:

$\widehat{\mathrm{AOD}}=\widehat{\mathrm{COE}}$ (hai góc đối đỉnh).

$\widehat{\mathrm{OAD}}=\widehat{\mathrm{OEC}}=90°$

Suy ra: ∆OAD $\infty$ ∆OEC (g.g)

$\Rightarrow \frac{\mathrm{OD}}{\mathrm{OC}}=\frac{\mathrm{AD}}{\mathrm{EC}}\Rightarrow \frac{5}{6}=\frac{4}{\mathrm{x}}\Rightarrow \mathrm{x}=\frac{4.6}{5}=\frac{24}{5}$

Áp dụng định lý py ta go vào tam giác ADO có:

AO² = OD² – DA² = 9 nên AO = 3.

Khi đó; AC = AO + OC = 3 + 6 = 9

Xét ∆OAD và ∆BAC có:

$\widehat{\mathrm{ADO}}=\widehat{\mathrm{ACB}}$ (cùng phụ với góc $\hat{\mathrm{B}}$).

$\widehat{\mathrm{OAD}}=\widehat{\mathrm{BAC}}=90°$

Suy ra: ∆OAD $\infty$ ∆BAC (g.g)

$$\begin{gathered} \Rightarrow \frac{\mathrm{AD}}{\mathrm{AC}}=\frac{\mathrm{OD}}{\mathrm{BC}} \\ \iff \frac{4}{9}=\frac{5}{\mathrm{BC}}\Rightarrow \mathrm{BC}=\frac{45}{4} \end{gathered}$$

Suy ra: $\mathrm{x}+\mathrm{y}=\frac{45}{4}\iff \frac{24}{5}+\mathrm{y}=\frac{45}{4}\Rightarrow \mathrm{y}=\frac{129}{20}$

Vậy $\mathrm{x}=\frac{24}{5}$ và $\mathrm{y}=\frac{129}{20}$

Bài 25. Cho tam giác ABC vuông tại A có chân đường cao AH chia cạnh huyền BC thành hai đoạn thẳng có độ dài lần lượt là HB = 16 cm và HC = 25 cm. Tính diện tích của tam giác ABC?

Lời giải:

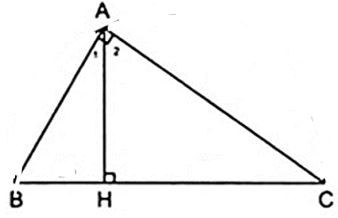
Xét tam giác AHB và tam giác CHA có:

$\widehat{\mathrm{AHB}}=\widehat{\mathrm{AHC}}=90°$

$\widehat{{\mathrm{A}}_1}=\hat{\mathrm{C}}$ (cùng phụ $\widehat{{\mathrm{A}}_2}$)

Suy ra: ∆AHB $\infty$ ∆CHA (g.g).

$\Rightarrow \frac{\mathrm{AH}}{\mathrm{HC}}=\frac{\mathrm{HB}}{\mathrm{HA}}$

Hay $\frac{\mathrm{HA}}{25}=\frac{16}{\mathrm{HA}}\iff {\mathrm{HA}}^2=400\Rightarrow \mathrm{HA}=20\left(\mathrm{cm}\right)$

Ta có: ${\mathrm{S}}_{\mathrm{ABC}}=\frac{1}{2}\mathrm{AH}.\mathrm{BC}=\frac{1}{2}.20.41=410\left({\mathrm{cm}}^2\right)$

Vậy diện tích tam giác ABC là 410 cm².

Bài 26. Cho tam giác ABC vuông tại A. Gọi H là hình chiếu vuông góc của A lên BC. Biết AB = 5cm; AC = 12cm.

a) Tính BH?

b) Chứng minh ∆AHB $\infty$ ∆CHA

Lời giải:

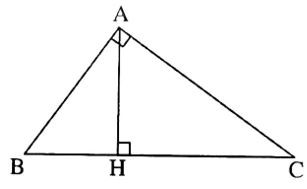
a) Áp dụng định lí Pyata go vào tam giác vuông ABC có:

BC² = AB² + AC² = 25 + 144= 169 nên BC = 13cm

Xét ∆ABC và ∆ HBA có:

$\widehat{\mathrm{BAC}}=\widehat{\mathrm{AHB}}=90°$

$\hat{\mathrm{B}}$ chung

Suy ra: ∆ABC $\infty$ ∆HBA (g.g)

$\Rightarrow \frac{\mathrm{AB}}{\mathrm{HB}}=\frac{\mathrm{BC}}{\mathrm{BA}}\Rightarrow \mathrm{HB}=\frac{{\mathrm{AB}}^2}{\mathrm{BC}}=\frac{5^2}{13}=\frac{25}{13}\mathrm{cm}$

b) Xét ∆AHB và ∆CHA có:

$\widehat{\mathrm{AHB}}=\widehat{\mathrm{AHC}}=90°$

$\widehat{\mathrm{BAH}}=\widehat{\mathrm{ACH}}$ (cùng phụ với góc $\widehat{\mathrm{HAC}}$)

Suy ra: ∆AHB $\infty$ ∆CHA (g.g).

Bài 27. Cho tam giác ABC vuông tại A. Dựng hai đường phân giác trong BH; CN của góc B và góc C. Hai đường này cắt nhau tại I. Gọi K là hình chiếu vuông góc của I lên BC. Chứng minh:

a) ∆IKC $\infty$ ∆NAC

b) ∆IKB $\infty$ ∆HAB.

Lời giải:

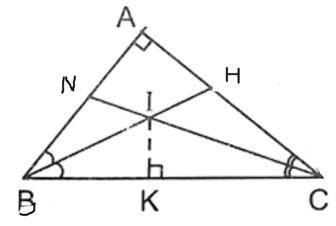
a) Xét ∆IKC và ∆NAC có:

$\widehat{\mathrm{IKC}}=\widehat{\mathrm{CAN}}=90°$

$\widehat{\mathrm{ICK}}=\widehat{\mathrm{NCA}}$ (vì CN là tia phân giác của $\widehat{\mathrm{ACB}}$)

Suy ra: ∆IKC $\infty$ ∆NAC (g.g) ( đpcm)

b) Xét ∆IKB và ∆HAB có:

$\widehat{\mathrm{IKB}}=\widehat{\mathrm{BAH}}=90°$

$\widehat{\mathrm{KBI}}=\widehat{\mathrm{ABH}}$ (vì BH là tia phân giác của $\widehat{\mathrm{ABC}}$)

Suy ra: ∆IKB $\infty$ ∆HAB (g.g) (đpcm)

Trắc nghiêm Toán 8 Bài 8: Ôn tập Chương 3

Bài 1: Cho biết $\frac{AB}{CD}=\frac{5}{7}$ và đoạn thẳng AB ngắn hơn đoạn thẳng CD là 10cm. Tính độ dài các đoạn thẳng AB, CD?

A. AB = 35cm, CD = 25cm

B. AB = 20cm, CD = 30cm

C. AB = 25cm, CD = 35cm

D. AB = 30cm, CD = 20cm

Hiển thị đáp án  

Đáp án: C

Giải thích:

Theo bài ra, ta có:$\frac{AB}{CD}=\frac{5}{7}$

 => AB =$\frac{5}{7}$ CD

Mà đoạn thẳng AB ngắn hơn đoạn thẳng CD là 10cm, suy ra: CD - AB = 10.

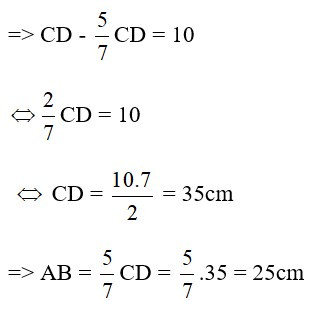
Bài 2: Cho ΔA’B’C’ ~ ΔABC. Biết S_A’B’C’ =$\frac{25}{49}$ S_ABC và hiệu 2 chu vi của 2 tam giác là 16m. Tính chu vi mỗi tam giác?

A. C_A’B’C’ = 30m, C_ABC = 46m

B. C_A’B’C’ = 56m, C_ABC = 40m

B. C_A’B’C’ = 24m, C_ABC = 40m

D. C_A’B’C’ = 40m, C_ABC = 56m

Hiển thị đáp án  

Đáp án: D

Giải thích:

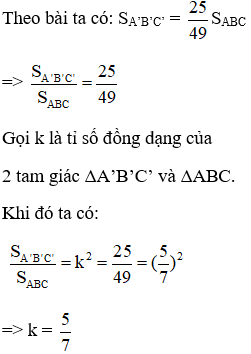
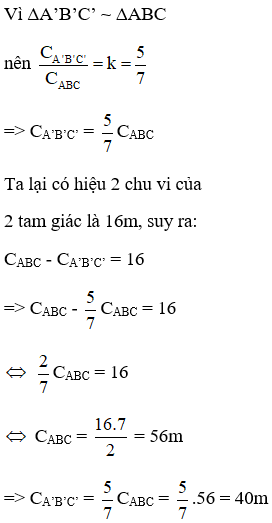
Vậy C_A’B’C’ = 40m, C_ABC = 56m

Bài 3: Cho hình vẽ biết DE // BC. Khẳng định nào sau đây là đúng?

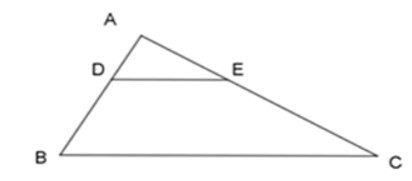
A. $\frac{AD}{AB}=\frac{AE}{AC}$

B. AD.AE = AB.AC

C. $\frac{AD}{DB}=\frac{DE}{BC}$

D. DE.AD = AB.BC

Hiển thị đáp án  

Đáp án: A

Giải thích:

Áp dụng hệ quả định lý Ta-lét,

ta có: $\frac{AD}{AB}=\frac{AE}{AC}=\frac{DE}{BC}$

=> Đáp án A đúng.

+ Vì $\frac{AD}{AB}=\frac{AE}{AC}$ nên AD.AC = AB.AE

=> Đáp án B sai.

+ Ta có: $\frac{DE}{BC}=\frac{AD}{AB}\ne \frac{AD}{DB}$ (hệ quả định lý Ta-lét)

=> Đáp án C sai.

+ Ta có: $\frac{AD}{DB}=\frac{DE}{BC}$ => AD.BC = AB.DE

=> Đáp án D sai.

Bài 4: Cho ΔABC vuông tại A, đường cao AH. Gọi I và K lần lượt là hình chiếu của H lên AB và AC. Tam giác AIK đồng dạng với tam giác nào dưới đây?

A. ACB

B. ABC

C. CAB

D. BAC

Hiển thị đáp án  

Đáp án: A

Giải thích:

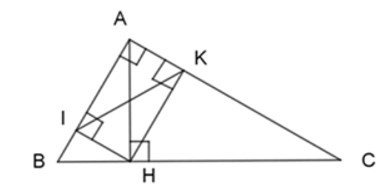
Gọi I, K lần lượt là hình chiếu của H lên AB và AC.

=>  $\widehat{HIA}=\widehat{HKA}=90°$

Xét tứ giác AIHK có: $\widehat{IAK}=\widehat{HIA}=\widehat{HKA}=90°$

 => Tứ giác AIHK là hình chữ nhật (dhnb)

+) Xét ΔAIK và ΔIAH ta có:

AI chung

AK = IH (theo tính chất của hình chữ nhật)

AH = IK (theo tính chất của hình chữ nhật)

=> ΔAIK = ΔIAH (c - c - c) (1)

Xét 2 tam giác vuông ΔIAH và ΔHAB có:

$\widehat{AIH}=\widehat{AHB}=90°$

Góc A chung

=> ΔIAH ~ ΔHAB (g - g) (2)

Xét 2 tam giác vuông ΔHAB và ΔACB có:

$\widehat{AHB}=\widehat{BAC}=90°$

Góc B chung

=> ΔHAB ~ ΔACB (g - g) (3)

Từ (1), (2) và (3) ta có: ΔAIK ~ ΔACB

Bài 5: Chỉ ra 1 tỉ số sai nếu áp dụng định lý Talet, biết ABCD là hình bình hành:

Hiển thị đáp án  

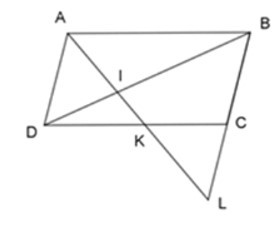
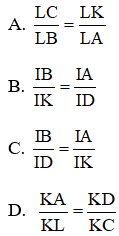
Đáp án: B

Giải thích:

Có CD // AB (vì ABCD là hình bình hành)

Suy ra: CK // AB; KD // AB; CL // AD

Vì CK // AB nên áp dụng định lý Talet

ta có: $\frac{LC}{LB}=\frac{LK}{LA}$

Vì KD // AB nên áp dụng định lý Talet ta có:

Có BC // AD (vì ABCD là hình bình hành)

Suy ra: CL // AD

Vì CL // AD nên áp dụng định lý Talet

ta có: $\frac{KA}{KL}=\frac{KD}{KC}$

Vậy $\frac{IB}{IK}=\frac{IA}{ID}$ sai

Bài 6: Cho biết ABCD là hình chữ nhật. Tìm x.

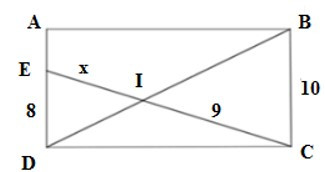
A. 7,2

B. 3,6

C. 14,4

D. 1,8

Hiển thị đáp án  

Đáp án: A

Giải thích:

Xét tam giác BCI và tam giác DEI có:

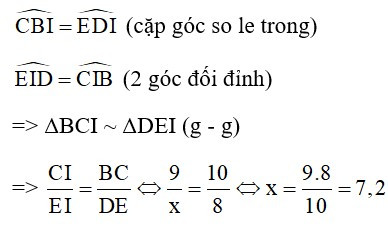
Vậy x = 7,2.

Bài 7: Cho hai tam giác MNP và QRS đồng dạng với nhau theo tỉ số k. Tỷ số diện tích của 2 tam giác MNP và QRS là:

A. k

B.$\frac{1}{k}$

C. k²

D. 2k

Hiển thị đáp án  

Đáp án: C

Giải thích:

Giả sử ΔMNP ~ ΔQRS theo tỉ số diện tích$\frac{S_{MNP}}{S_{QRS}}=k^2$

Bài 8: Cho ΔMNP ~ ΔHGK có tỉ số chu vi: $\frac{P_{MNP}}{P_{HGK}}=\frac{2}{7}$ khi đó:

Hiển thị đáp án  

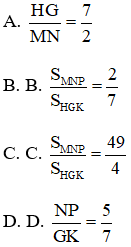
Đáp án: A

Giải thích:

Gọi k là tỉ số đồng dạng của 2 tam giác MNP và HGK

Theo bài ra ta có ΔMNP ~ ΔHGK 

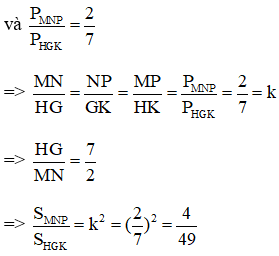
Bài 9: Chỉ ra câu sai?

A. ΔABC = ΔA’B’C’ => ΔABC ~ ΔA’B’C’

B. $\widehat{A}=\widehat{A\text{'}},\widehat{B}=\widehat{B\text{'}}$ => ΔABC ~ ΔA’B’C’

C. $\frac{AB}{A\text{'}B\text{'}}=\frac{BC}{B\text{'}C\text{'}}$ => ΔABC ~ ΔA’B’C’

D. ΔABC = ΔA’B’C’ => S_ABC = S_A’B’C’

Hiển thị đáp án  

Đáp án: C

Giải thích:

Giả sử ta có: ΔABC = ΔA’B’C’

=> $\widehat{A}=\widehat{A\text{'}},\widehat{B}=\widehat{B\text{'}}$ (các cặp góc tương ứng bằng nhau)

=> ΔABC ~ ΔA’B’C’ (g - g)

=> Đáp án A, B đúng

+ Giả sử xét 2 tam giác ABC và tam giác A’B’C’ có: $\frac{AB}{A\text{'}B\text{'}}=\frac{BC}{B\text{'}C\text{'}}$

Điều kiện trên chưa đủ để chứng minh ΔABC ~ ΔA’B’C’.

=> Đáp án C sai.

+ Vì hai tam giác bằng nhau thì có diện tích bằng nhau => Đáp án D đúng.

Bài 10: Cho ΔABC có AB = 4cm, BC = 6cm, AC = 5cm.

ΔMNP có MN = 3cm, NP = 2,5cm, PM = 2cm

thì tỉ lệ $\frac{S_{MNP}}{S_{ABC}}$ bằng bao nhiều?

A. $\frac{1}{3}$

B. $\frac{1}{4}$

C. $\frac{1}{8}$

D. 1

Hiển thị đáp án  

Đáp án: B

Giải thích:

Ta có:

Xem thêm các bài tổng hợp lý thuyết Toán lớp 8 đầy đủ, chi tiết khác:

Lý thuyết Hình hộp chữ nhật

Lý thuyết Hình hộp chữ nhật (tiếp)

Lý thuyết Thể tích của hình hộp chữ nhật

Lý thuyết Hình lăng trụ đứng

Lý thuyết Diện tích xung quanh của hình lăng trụ