Nội dung bài viết

    Xem thêm

    Lý thuyết Trường hợp đồng dạng thứ ba (mới 2023 + Bài Tập) – Toán 8

    Lý thuyết Trường hợp đồng dạng thứ ba lớp 8 gồm lý thuyết chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm Toán 8 Bài 7: Trường hợp đồng dạng thứ ba.

    1 1,404 25/02/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Lý thuyết Toán 8 Bài 7: Trường hợp đồng dạng thứ ba

    Bài giảng Toán 8 Bài 7: Trường hợp đồng dạng thứ ba

    A. Lý thuyết

    1. Định lí

    - Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.

    - Ví dụ 1. Cho tam giác ABC và các đường cao BH, CK. Chứng minh ∆ABH ∞ ∆ ACK.  

    Lời giải:

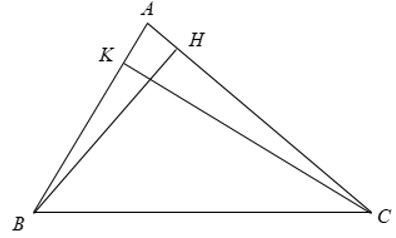
    Lý thuyết Trường hợp đồng dạng thứ ba chi tiết – Toán lớp 8 (ảnh 1)

    Xét ∆ABH và ∆ACK có:

    A^ chungAHB^=AKC^=90°

    Suy ra: ∆ABH ∞ ∆ACK.

    B. Bài tập tự luyện

    Bài 1. Cho hình bên, ABCD là hình thang (AB// CD) có AB = 12 cm; CD = 27cm DAB^=DBC^. Tính độ dài đoạn BD gần nhất bằng bao nhiêu?

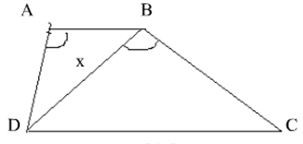
    Lý thuyết Trường hợp đồng dạng thứ ba chi tiết – Toán lớp 8 (ảnh 1)

    Lời giải:

    Xét ∆ABD và ∆BDC có:

    BAD^=DBC^ABD^=BDC^

    Suy ra: ∆ABD ∞ ∆BDC (g.g). 

    ⇒ABBD=ADBC=BDDChay

    12x=x27⇒x2=12.27=324

    ⇔x=18

    Vậy BD = 18cm.

    Bài 2. Cho góc xOy khác góc bẹt. Trên tia Ox lấy 2 điểm A và B sao cho: OA = 5cm; OB = 16cm. Trên tia Oy, lấy hai điểm C và D sao cho OC = 8cm; OD =10cm.

    a) Chứng minh ∆OCB ∞ ∆OAD.

    b) Gọi I là giao điểm của các cạnh AD và BC. Chứng minh rằng ∆IBA ∞∆ IDC

    Lời giải:

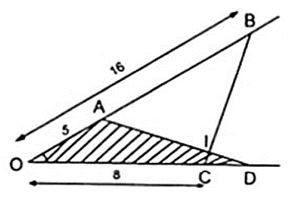
    Lý thuyết Trường hợp đồng dạng thứ ba chi tiết – Toán lớp 8 (ảnh 1)

    a) Xét ∆OCB và ∆ OAD có

    O^ chungOCOA=OBOD85=1610

    Suy ra: ∆OCB ∞∆OAD (c.g.c)

    b)  Theo a ta có: ∆OCB ∞∆OAD

    ⇒ADO^=CBO^ hay IDC^=IBA^ (1)

    Mà CID^=AIB^ (vì đối đỉnh) (2)

    Từ (1) và (2) suy ra: ∆IBA ∞ ∆IDC (g.g)

    Bài 3. Tìm x, y trong hình vẽ sau:

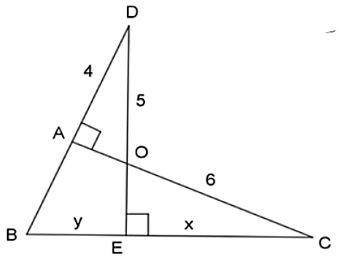
    Lý thuyết Trường hợp đồng dạng thứ ba chi tiết – Toán lớp 8 (ảnh 1)

    Lời giải:

    Xét ∆OAD và ∆OEC có:

    AOD^=COE^ (hai góc đối đỉnh).

    OAD^=OEC^=90°

    Suy ra: ∆OAD ∞ ∆OEC (g.g)

    ⇒ODOC=ADEC⇒56=4x⇒x=4.65=245

    Áp dụng định lý py ta go vào tam giác ADO có:

    AO2 = OD2 – DA2 = 9 nên AO = 3.

    Khi đó; AC = AO + OC = 3 + 6 = 9

    Xét ∆OAD và ∆BAC có:

    ADO^=ACB^ (cùng phụ với góc B^).

    OAD^=BAC^=90°

    Suy ra: ∆OAD ∞ ∆BAC (g.g)

    ⇒ADAC=ODBC⇔49=5BC⇒BC=454

    Suy ra: x+y=454⇔245+y=454⇒y=12920

    Trắc nghiệm Toán 8 Bài 7: Trường hợp đồng dạng thứ ba của tam giác

    Bài 1: Tam giác ABC có A ^=2B^, AC = 16cm, BC = 20cm. Tính độ dài cạnh AB.

    A. 18cm

    B. 20cm

    C. 15cm

    D. 9cm

    Đáp án: D

    Giải thích:

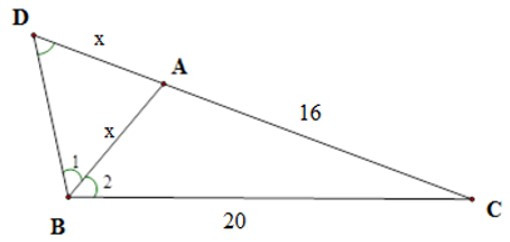
    Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 2)

    Trên tia đối của tia AC lấy điểm D sao cho AD = AB.

    Tam giác ABD cân tại A 

    Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 3)

    Bài 2: Cho tam giác ABC vuông tại A có: AB = 5, AC = 12. Trên cạnh BC lấy điểm M

    sao cho BM = 513 BC. Qua M kẻ đường thẳng vuông góc với AC tại N. Độ dài MN là:

    A. 1213

    B. 4513

    C. 4013

    D. 12

    Đáp án: C

    Giải thích:

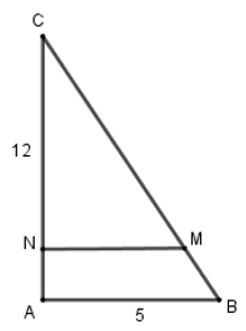
    Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 5)

    Tam giác ABC vuông tại A, theo định lí Pi-ta-go ta có:

    BC2 = AB2 + AC2

    => BC2 = 52 + 122 = 169

    => BC = 13

    BM = BC = .13 = 5

    => CM = 13 - 5 = 8.

    Xét ΔCMN và ΔCBA có:

    N = A = 900 (gt)

    Góc C chung

    => ΔCMN ~ ΔCBA (g - g)

    Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 6)

    Bài 3: Cho hình thang vuông ABCD (A ^=D ^=900)

    có BC  BD, AB = 4cm, CD = 9cm. Độ dài BD là:

    A. 8cm

    B. 12cm

    C. 9cm

    D. 6cm

    Đáp án: D

    Giải thích:

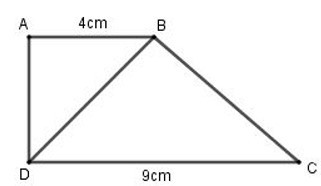
    Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 7)

    Xét tam giác ABD và BDC có:

    Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 8)

    => BD2 = AB.CD = 4.9 = 36

    => BD = 6.

    Bài 4: Cho hai tam giác ABC và FED có A ^=F^, cần thêm điều kiện gì dưới đây để hai tam giác (thứ tự đỉnh như vậy) đồng dạng theo trường hợp góc - góc?

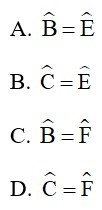
    Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 9)

    Đáp án: A

    Giải thích:

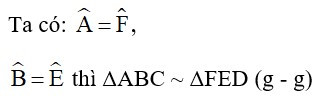
    Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 10)

    Bài 5: Tính giá trị của x trong hình dưới đây:

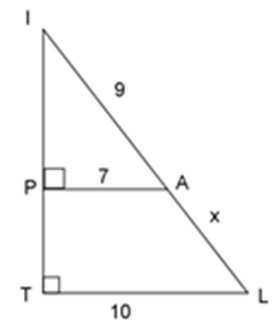
    Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 11)

    A. x = 3

    B.x = 277

    C. x = 4

    D. x =275

    Đáp án: B

    Giải thích:

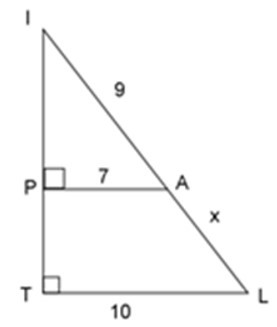
    Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 12)

    Xét ΔIPA và ΔITL ta có:

    +) IPA = ITL = 900

    +) Góc TIL chung

    => ΔIPA ~ ΔITL (g - g)

    =>PATL=IAIL⇔PATL=IAIA+AL

    ⇔710=99+x

    ⇔x=277

    Bài 6: Tam giác ABC có A ^=2B^, AB = 11cm, AC = 25cm. Tính độ dài cạnh BC.

    A. 30cm

    B. 20cm

    C. 25cm

    D. 15cm

    Đáp án: A

    Giải thích:

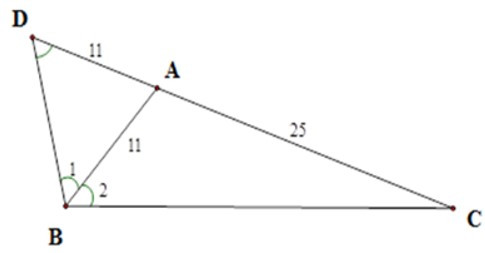
    Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 14)

    Trên tia đối của tia AC lấy điểm D sao cho AD = AB.

    Tam giác ABD cân tại A 

    Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 15)

    Từ đó BC2 = 25.36 suy ra BC = 5.6 = 30(cm)

    Bài 7: Nếu 2 tam giác ABC và DEF có A^=70°,C^=60°,E^=50°,F^=70° thì chứng minh được:

    A.ΔABC ~ ΔFED

    B. ΔACB ~ ΔFED

    C. ΔABC ~ ΔDEF

    D. ΔABC ~ ΔDFE

    Đáp án: A

    Giải thích:

    Xét ΔABC có:  

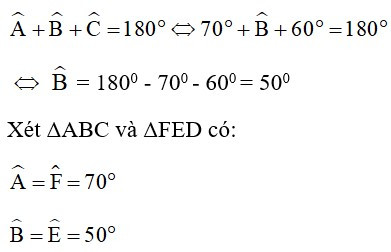
    Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 16)

     => ΔABC ~ ΔFED (g - g)

    Bài 8: Cho tam giác ABC cân tại A. Trên cạnh AC lấy điểm M, trên đoạn thẳng BM lấy điểm K sao cho góc BCK^=ABM^ .

    1. Tam giác MBC đồng dạng với tam giác

    A. MCK

    B. MKC

    C. KMC

    D. CMK

    Đáp án: A

    Giải thích:

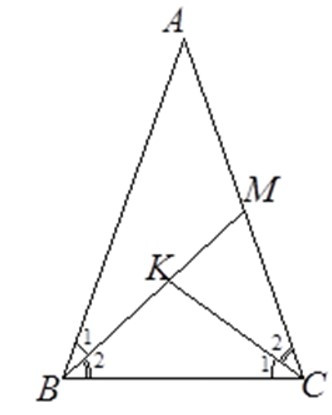
    Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 17)

    Tam giác ABC cân tại A 

    Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 18)

    Do đó ΔMBC ~ ΔMCK (g.g).

    2. Tính MB.MK bằng

    A. 2MC2

    B. CA2

    C. MC2

    D. BC2

    Đáp án: C

    Giải thích:

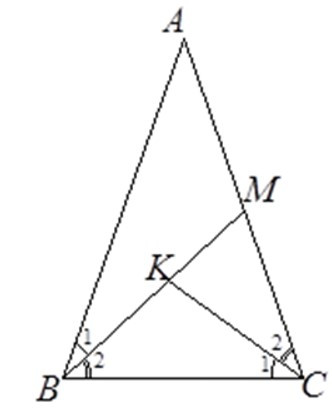
    Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 19)

    Vì ΔMBC ~ ΔMCK nên MCMK=MBMC (hai cạnh tương ứng tỉ lệ)

    Suy ra MC2 = MB.MK

    Bài 9: Cho hình thang ABCD (AB // CD) có góc ADB^=BCD^, AB = 2cm, BD = 5cmm, ta có:

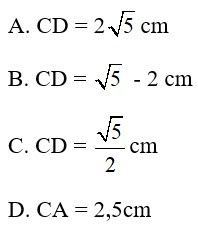
    Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 20)

    Đáp án: D

    Giải thích:

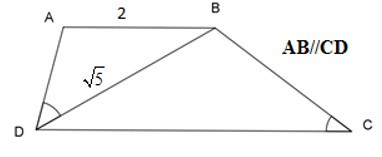
    Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 21)

    Vì AB // CD nên: ABD^=BDC^ (cặp góc so le trong)

    Xét ΔADB và ΔBCD ta có:

    ABD^=BDC^ (chứng minh trên)

    ADB^=BCD^ (theo gt)

    => ΔADB ~ ΔBCD (g - g)

    => ABBD=DBCD⇔25=5CD

    ⇔CD=5.52=52 = 2,5 cm

    Bài 10: Cho ΔABC có các đường cao BD và CE cắt nhau tại H. Gọi M là giao của AH với BC.

    1. Chọn câu đúng.

    A. ΔHBE ~ ΔHCD

    B. ΔABD ~ ΔACE

    C. Cả A, B đều đúng

    D. Cả A, B đều sai

    Đáp án: C

    Giải thích:

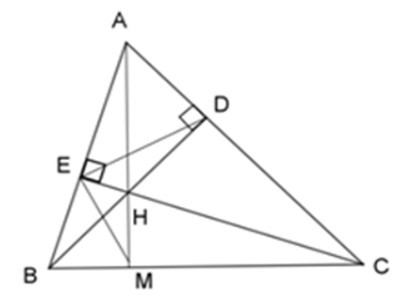
    Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 23)

    Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 1)

    2. Chọn khẳng định sai.

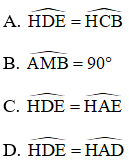
    Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 1)

    Đáp án: D

    Giải thích:

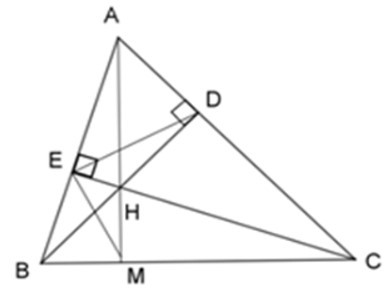
    Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 26)

    Theo cmt ta có: ΔHBE ~ ΔHCD

    Xét ΔHED và ΔHBC ta có:

    Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 27)

    Từ (1) và (2) ta có: HDE^=HAE^ nên A, B, C đúng, D sai.

    Xem thêm các bài tổng hợp lý thuyết Toán lớp 8 đầy đủ, chi tiết khác:

    Lý thuyết Các trường hợp đồng dạng của tam giác vuông

    Lý thuyết Ôn tập chương 3

    Lý thuyết Hình hộp chữ nhật

    Lý thuyết Hình hộp chữ nhật (tiếp)

    Lý thuyết Thể tích của hình hộp chữ nhật

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,404 25/02/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: