Lý thuyết Diện tích xung quanh của hình chóp đều (mới 2023 + Bài Tập) – Toán 8
Lý thuyết Diện tích xung quanh của hình chóp đều lớp 8 gồm lý thuyết chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm Toán 8 Bài 8: Diện tích xung quanh của hình chóp đều.
Lý thuyết Toán 8 Bài 8: Diện tích xung quanh của hình chóp đều
Bài giảng Toán 8 Bài 8: Diện tích xung quanh của hình chóp đều
A. Lý thuyết.
1. Công thức tính diện tích xung quanh của hình chóp đều
- Diện tích xung quanh của hình chóp đều bằng tích của nửa chu vi đáy với trung đoạn:
Sxq = p.d (trong đó p: nửa chu vi đáy, d: trung đoạn)
- Diện tích toàn phần của hình chóp
Diện tích toàn phần của hình chóp bằng tổng của diện tích xung quanh và diện tích đáy:
Stp = Sxq + S (trong đó S: diện tích đáy)
- Ví dụ 1. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông, cạnh đáy là 3cm, chiều cao 5cm.
a) Tính diện tích xung quanh của hình chóp.
b) Tính diện tích toàn phần của hình chóp.
Lời giải:
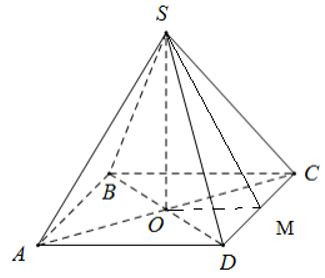
a) Ta có ABCD là hình vuông, khi đó nửa chu vi bằng: .
Kẻ SM vuông góc với CD.
Do tam giác SCD cân tại S nên SM cũng là đường trung tuyến
Suy ra M là trung điểm của CD.
Xét tam giác ACD, có:
O là trung điểm của AC
M là trung điểm của CD
Suy ra OM là đường trung bình của tam giác ACD
Xét tam giác SOM vuông tại O, có:
Diện tích xung quanh của hình chóp đều là:
b) Diện tích đáy là: S = 32 = 9 cm2
+ Diện tích toàn phần của hình chóp đều là
B. Bài tập tự luyện
Bài 1. Cho hình chóp tứ giác đều có các mặt bên là tam giác đều cạnh 6cm. Tính diện tích toàn phần của hình chóp?
Lời giải:
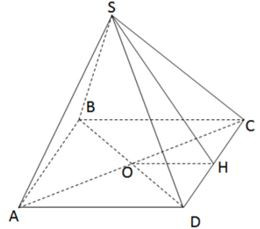
Do mặt bên của hình chóp là tam giác đều cạnh 6cm nên đáy là hình vuông cạnh 6cm.
Nửa chu vi đáy là
Các mặt bên là tam giác đều cạnh 6cm nên độ dài trung đoạn là
Diện tích xung quanh là
Diện tích đáy là: 62 = 36cm2
Diện tích toàn phần là:
Bài 2. Một hình chóp tứ giác đều S.ABCD có độ dài cạnh bên là 5cm và đáy là hình vuông cạnh 8cm.Tính diện tích xung quanh của hình chóp?
Lời giải:
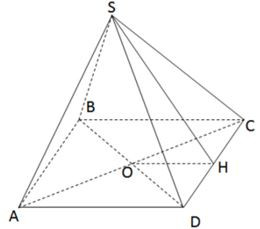
Nửa chu vi đáy là:
Gọi H là trung điểm của CD, suy ra: CH = DH = 4cm
Áp dụng định lí Pytago vào tam giác vuông SHC có:
SH2 = SC2 – CH2 = 52 – 42 = 9 nên SH = 3cm
Diện tích xung quanh của hình chóp là;
Sxq= p. SH = 16. 3 = 48 cm2
Bài 3. Một hình chóp đều có độ dài cạnh bên là 13cm, đáy là tam giác đều ABC. Biết độ dài trung đoạn bằng 12 cm. Tính diện tích xung quanh của hình chóp.
Lời giải:
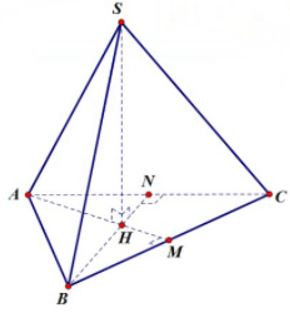
Gọi M là trung điểm của BC.
Theo giả thiết ta có: SM = 12 cm; SC = 13cm
Áp dụng định lí Pytago vào tam giác vuông SMC có:
MC2 = SC2 – SM2 = 132 – 122 = 25
Suy ra: MC = 5cm.
Vì M là trung điểm BC nên BC = 2MC = 10cm.
Vì đáy là tam giác đều nên AB = BC= CA = 10cm
Nửa chu vi đáy là
Diện tích xung quanh là: Sxq = p.d = 15. 12 = 180cm2.
Trắc nghiệm Toán 8 Bài 8: Diện tích xung quanh hình chóp đều
Bài 1: Tính diện tích xung quanh của hình chóp cụt tứ giác đều có các cạnh đáy bằng 10cm và 15cm, chiều cao của mặt bên bằng 12cm.
A. 300cm2
B. 1200cm2
C. 150cm2
D. 600cm2
Đáp án: D
Giải thích:
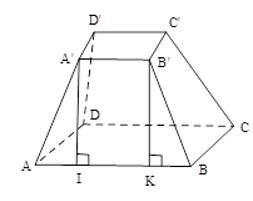
Mặt bên hình chóp cụt tứ giác đều là hình thang cân nên diện tích một mặt bên
bằng = 150 (cm2)
Hình chóp cụt tứ giác đều có 4 mặt bên bằng nhau nên diện tích xung quanh bằng
150.4 = 600 (cm2)
Bài 2: Diện tích xung quanh hình chóp đều được tính theo công thức:
A. Tích nửa diện tích đáy và chiều cao
B. Tích nửa chu vi đáy và trung đoạn
C. Tích chu vi đáy và chiều cao
D. Tổng chu vi đáy và trung đoạn
Đáp án: B
Giải thích:
Diện tích xung quanh hình chóp đều bằng tích của nửa chu vi đáy và trung đoạn.
Bài 3: Cho hình chóp tứ giác đều SABCD, có đáy là hình vuông cạnh 2cm. Các mặt bên là các tam giác cân có đường cao bằng 7cm. Tính diện tích toàn phần của hình chóp SABCD.

Đáp án: B
Giải thích:
Diện tích đáy là diện tích hình vuông nên ta có:
Diện tích xung quanh là:
Diện tích toàn phần là:
Bài 4: Tính diện tích xung quanh của hình chóp cụt tứ giác đều có các cạnh đáy bằng 6cm và 8cm, chiều cao của mặt bên bằng 5cm.
A. 120cm2
B. 70cm2
C. 150cm2
D. 140cm2
Đáp án: D
Giải thích:
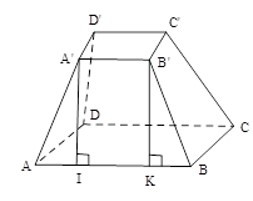
Mặt bên hình chóp cụt tứ giác đều là hình thang cân nên diện tích một mặt bên bằng
= 35(cm2)
Hình chóp cụt tứ giác đều có 4 mặt bên bằng nhau nên diện tích xung quanh bằng
35.4 = 140 (cm2)
Bài 5: Diện tích xung quanh của hình chóp đều bằng
A. Tích nửa chu vi đáy và đường cao của hình chóp
B. Tích nửa chu vi đáy và trung đoạn
C. Tích chu vi đáy và trung đoạn
D. Tổng chu vi đáy và trung đoạn
Đáp án: B
Giải thích:
Diện tích xung quanh của hình chóp đều bằng tích của nửa chu vi đáy và trung đoạn.
Bài 6: Cho hình chóp tam giác đều S.ABC có các mặt là các tam giác đều. Biết diện tích của mặt đáy bằng . Tính diện tích xung quanh hình chóp
A. 60 (cm2)
B. 20 (cm2)
C. 30(cm2)
D. 40 (cm2)
Đáp án: A
Giải thích:
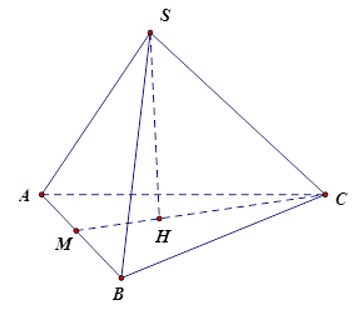
Do SABC là hình chóp tam giác đều nên hình chóp có tất cả các mặt bằng nhau nên diện tích bằng nhau cùng bằng
Diện tích xung quanh là:
Bài 7: Một kim tự tháp có dạng là một hình chóp tứ giác đều có diện tích xung quanh bằng 320m2, các mặt bên là các tam giác đều. Biết đường cao của một mặt bên là 20m. Hãy tính cạnh của đáy.
A. 8m
B. 16m
C. 32m
D. 48m
Đáp án: A
Giải thích:
Gọi độ dài cạnh đáy là x
Do tất cả các mặt bên là tam giác đều nên cạnh của các mặt bên cũng bằng x
Diện tích một mặt bên là:
Khi đó diện tích xung quanh là:
Theo đầu bài ta có:
Bài 8: Cho hình chóp tam giác đều S.ABC có các mặt là các tam giác đều. Gọi SH là đường cao của hình chóp, HC = cm. Tính diện tích xung quanh hình chóp
Đáp án: C
Giải thích:
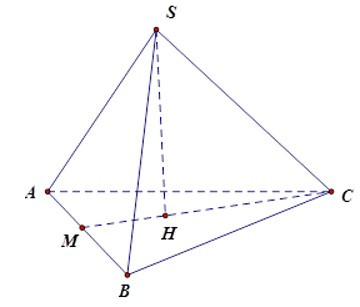
Gọi M là giao điểm của CH và AB ta có CM AB và AM = BM. Vì H là trọng tâm ΔABC
nên CM = CH
= (cm)
Đặt AB = BC = x,
ta có BC2 - MB2 = CM2 (định lý Pytago cho ΔMBC)
nên hay
Suy ra x = 6. Vậy BA = 6cm.
Bài 9: Cho hình chóp tam giác đều S.ABC có các mặt là các tam giác đều. Gọi SH là đường cao của hình chóp, HC = cm.
1. Độ dài cạnh hình chóp là:
A. 9cm
B. 3cm
C. 6cm
D. 12cm
Đáp án: A
Giải thích:
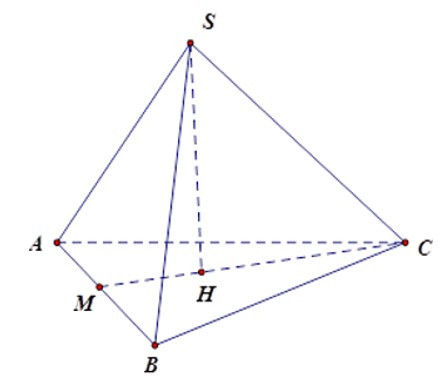
Gọi M là giao điểm của CH và AB ta có CM AB và AM = BM. Vì H là trọng tâm ΔABC
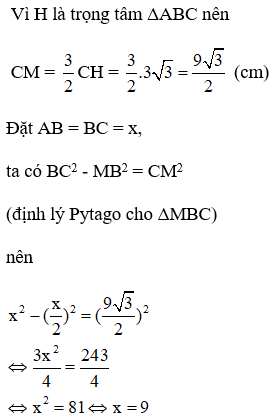
Vậy các cạnh của hình chóp có độ dài là 9cm.
2. Tính diện tích xung quanh hình chóp (làm tròn đến một chữ số thập phân)
A. 105(cm2)
B. 105,2(cm2)
C. 210,4(cm2)
D. 108(cm2)
Đáp án: B
Giải thích:
Xét tam giác SAB và CAB là hai tam giác đều có cạnh bằng nhau nên SM = CM
=> SM = CM = cm
Sxq == pd = (cm2)
Bài 10: Tính thể tích của hình chóp tam giác đều có tất cả các cạnh đều bằng 6cm (làm tròn đến chữ số thập phân thứ hai).
A. 24,64cm3
B. 25,46cm3
C. 26,46cm3
D. 26,64cm3
Đáp án: B
Giải thích:
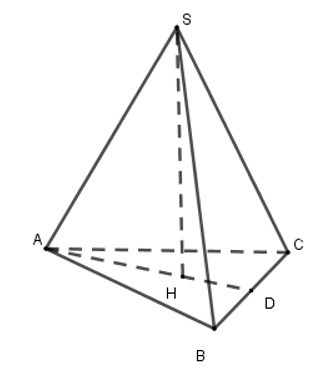
Chóp tam giác đều S.ABC có SH (ABC) nên H là trọng tâm tam giác ABC và D là trung điểm BC.
Áp dụng định lý Pytago cho tam giác ABD vuông tại D ta có


Xem thêm các bài tổng hợp lý thuyết Toán lớp 8 đầy đủ, chi tiết khác:
Lý thuyết Thể tích của hình lăng trụ
Lý thuyết Hình chóp đều và hình chóp cụt đều
Lý thuyết Diện tích xung quanh của hình chóp đều
Xem thêm các chương trình khác:
- Tóm tắt tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 8 (hay nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Soạn văn 8 (ngắn nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Văn mẫu lớp 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Hóa học 8
- Giải sbt Hóa học 8
- Giải vở bài tập Hóa học 8
- Lý thuyết Hóa học 8
- Các dạng bài tập Hóa học lớp 8
- Giải sgk Vật Lí 8
- Giải sbt Vật Lí 8
- Lý thuyết Vật Lí 8
- Giải vở bài tập Vật lí 8
- Giải sgk Tiếng Anh 8 (sách mới) | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2
- Giải sgk Tiếng Anh 8 | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2 (sách mới)
- Giải sbt Tiếng Anh 8 (sách mới) | Sách bài tập Tiếng Anh 8
- Giải sbt Tiếng Anh 8 (thí điểm)
- Giải sgk Tin học 8 | Giải bài tập Tin học 8 Học kì 1, Học kì 2 (sách mới)
- Giải sgk Lịch Sử 8 | Giải bài tập Lịch sử 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Lịch sử 8 (sách mới) | Kiến thức trọng tâm Lịch sử 8
- Giải vở bài tập Lịch sử 8
- Giải Tập bản đồ Lịch sử 8
- Đề thi Lịch Sử 8
- Giải vở bài tập Sinh học 8
- Giải sgk Sinh học 8
- Lý thuyết Sinh học 8
- Giải sgk Giáo dục công dân 8 | Giải bài tập Giáo dục công dân 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Giáo dục công dân 8 (sách mới) | Kiến thức trọng tâm GDCD 8
- Lý thuyết Địa Lí 8 (sách mới) | Kiến thức trọng tâm Địa Lí 8
- Giải sgk Địa Lí 8 | Giải bài tập Địa Lí 8 Học kì 1, Học kì 2 (sách mới)
- Giải Tập bản đồ Địa Lí 8
- Đề thi Địa lí 8
