Nội dung bài viết

    Xem thêm

    Lý thuyết Bất phương trình một ẩn (mới 2023 + Bài Tập) – Toán 8

    Lý thuyết Bất phương trình một ẩn lớp 8 gồm lý thuyết chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm Toán 8 Bài 3: Bất phương trình một ẩn.

    1 5,452 25/02/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Lý thuyết Toán 8 Bài 3: Bất phương trình một ẩn

    Bài giảng Toán 8 Bài 3: Bất phương trình một ẩn

    A. Lý thuyết

    1. Bất phương trình một ẩn

    - Định nghĩa bất phương trình một ẩn: Bất phương trình ẩn x là hệ thức A (x) > B (x) hoặc A (x) < B (x) hoặc A (x) ≥ B (x) hoặc A (x) ≤ B (x).

    Trong đó: A (x) gọi là vế trái; B(x) gọi là vế phải.

    Ví dụ 1.

    7x – 1 > 3x là bất phương trình với ẩn x;

    2 – 6y = 3(y + 2) – 1 là bất phương trình với ẩn y;

    2t – 9 = 2 + 5(t + 6) là bất phương trình với ẩn t.

    - Nghiệm của bất phương trình là giá trị của ẩn để khi thay vào bất phương trình ta được một khẳng định đúng.

    Ví dụ 2. Cho bất phương trình 4 + 3x > 2(x + 1) – 7  (1).

    Với x = 1, ta có:

    VT(1) = 4 + 3 . 1 = 7;

    VP(1) = 2 . (1 + 1) – 7 = 2 . 2 – 7 = – 3.

    Nhận thấy x = 1 thỏa mãn bất phương trình (1) nên x = 1 là nghiệm (hay nghiệm đúng) của bất phương trình (1).

    2. Tập nghiệm của bất phương trình

    - Tập hợp tất cả các nghiệm của một bất phương trình được gọi là tập nghiệm của bất phương trình đó.

    - Giải bất phương trình là tìm tất cả các nghiệm của bất phương trình đó.

    Ví dụ 3. Tập nghiệm của bất phương trình x < −3 là tập hợp các số nhỏ hơn −3, tức là tập hợp {x | x < −3}.

    Ta biểu diễn tập hợp này trên trục số như hình vẽ:

    Lý thuyết Bất phương trình một ẩn chi tiết – Toán lớp 8 (ảnh 1)

    Ví dụ 4. Tập nghiệm của bất phương trình x ≥ 5 là tập hợp các số lớn hơn hoặc bằng 5 tức là tập hợp {x | x ≥ 5}.

    Ta biểu diễn tập hợp này trên trục số như hình vẽ:

    Lý thuyết Bất phương trình một ẩn chi tiết – Toán lớp 8 (ảnh 1)

    3. Bất phương trình tương đương

    - Hai bất phương trình tương đương nếu chúng có cùng một tập nghiệm.

    - Để chỉ hai phương trình tương đương, ta dùng kí hiệu “” (đọc là tương đương).

    Ví dụ 5. Hai phương trình x – 4 > 0 và x > 4 được gọi là tương đương với nhau vì chúng có cùng tập nghiệm là {x | x > 4}. Khi đó ta viết: x – 4 > 0⇔x > 4. 

    B. Bài tập tự luyện

    Bài 1. Kiểm tra xem giá trị x = 2 là nghiệm của bất phương trình nào trong các bất phương trình sau:

    a) 2x – 5 < 10

    b) −4x > 3x + 7

    c) 5 – 2x > 4x – 6

    Lời giải:

    Thay x = 2 lần lượt vào từng vế của mỗi bất phương trình, ta được:

    a) 2x – 5 = 2 . 2 – 5 = –1 < 10.

    Vậy x = 2 là nghiệm của bất phương trình 2x + 3 < 9.

    b) – 4x = – 4 . 2 = – 8;

    3x + 7 = 3 . 2 + 7 = 13

    Vì – 8 < 13 nên x = 2 không phải nghiệm của bất phương trình −4x > 3x + 7.

    c) 5 – 2x > 4x – 6

    5 – 2x = 5 – 2 . 2 = 1;

    4x – 6 = 4 . 2 – 6 = 2.

    Vì 1 < 2 nên x = 2 không phải là nghiệm của bất phương trình 5 – x > 3x – 12.

    Bài 2. Viết và biểu diễn tập nghiệm trên trục số bất phương trình x ≤ −6.

    Lời giải:

    Tập nghiệm của bất phương trình x ≤ −6 là tập hợp các số nhỏ hơn hoặc bằng −6, tức là tập hợp {x | x ≤ −6}.

    Ta biểu diễn tập hợp này trên trục số như hình vẽ:

    Lý thuyết Bất phương trình một ẩn chi tiết – Toán lớp 8 (ảnh 1)

    Bài 3. Hình vẽ sau đây biểu diễn tập nghiệm của bất phương trình nào? (Chỉ nêu một bất phương trình).

    a) 

    Lý thuyết Bất phương trình một ẩn chi tiết – Toán lớp 8 (ảnh 1)

    b)

    Lý thuyết Bất phương trình một ẩn chi tiết – Toán lớp 8 (ảnh 1)

    c)

    Lý thuyết Bất phương trình một ẩn chi tiết – Toán lớp 8 (ảnh 1)

    Lời giải:

    a) Hình a) biểu diễn tập nghiệm của bất phương trình x > 4;

    b) Hình b) biểu diễn tập nghiệm của bất phương trình x < −5;

    c) Hình c) biểu diễn tập nghiệm của bất phương trình x ≥ 2.

    Trắc nghiệm Toán 8 Bài 3: Bất phương trình một ẩn

    Bài 1: Với điều kiện nào của x thì biểu thức

    B =2x−43−x  nhận giá trị âm?

    A. x < -2

    B. x < 2 hoặc x > 3

    C. x > 2

    D. 2 < x < 3

    Đáp án: A

    Giải thích:

    Ta có: B = 2x−43−x < 0

    ⇔2x−4>03−x<02x−4<03−x>0⇔x>2x>3x<2x<3⇔x<2x>3

    Vậy với x<2x>3 thì B âm.

    Đáp án cần chọn là: B

    Bài 2: Bất phương trình x - 2 > 4, phép biến đổi nào sau đây là đúng?

    A. x > 4 - 2

    B. x > -4 + 2

    C. x > -4 -2

    D. x > 4 + 2

    Đáp án: D

    Giải thích:

    Ta có x - 2 > 4, chuyển -2 từ vế trái sang

    vế phải ta được x > 4 + 2.

    Bài 3: Hãy chọn câu đúng,

    x = -3 là một nghiệm của bất phương trình?

    A. 2x + 1 > 5

    B. 7 - 2x < 10 - x

    C. 2 + x < 2 + 2x

    D. -3x > 4x + 3

    Đáp án: D

    Giải thích:

    + Thay x = -3 vào bất phương trình 2x + 1 > 5 ta được

    2. (-3) + 1 > 5 ⇔ -5 > 5 (vô lý)

    nên x = -3 không là nghiệm của bất phương trình 2x + 1 > 5.

    + Thay x = -3 vào bất phương trình 7 - 2x < 10 - x ta được

    7 - 2. (-3) < 10 - (-3)

    ⇔ 13 < 13 (vô lý) nên x = -3

    không là nghiệm của bất phương trình 7 - 2x < 10 - x.

    + Thay x = -3 vào bất phương trình 2 + x < 2 + 2x ta được

    2 + (-3) < 2 + 2. (-3)

    ⇔ -1 < -4 (vô lý) nên x = -3

    không là nghiệm của bất phương trình 2 + x < 2 + 2x.

    + Thay x = -3 vào bất phương trình -3x > 4x + 3 ta được

    -3. (-3) > 4. (-3) + 3

    ⇔ 9 > -9 (luôn đúng) nên x = -3

    là nghiệm của bất phương trình -3x > 4x + 3.

    Bài 4: Biểu diễn tập nghiệm của

    bất phương trình x ≥ 8 trên trục số, ta được?

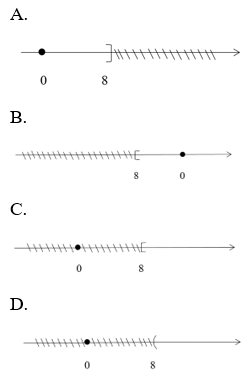
    Trắc nghiệm Bất phương trình một ẩn có đáp án - Toán lớp 8 (ảnh 1)

    Đáp án: C

    Giải thích:

    Ta biểu diễn x ≥ 8 trên trục số như sau:

    Trắc nghiệm Bất phương trình một ẩn có đáp án - Toán lớp 8 (ảnh 4)

    Bài 5: Bất phương trình (x + 2)2 < x + x2 - 3 có nghiệm là?

    A. x >-73

    B. x > 73

    C. x < -73

    D. x >73

    Đáp án: C

    Giải thích:

    (x + 2)2 < x + x2 - 3

    ⇔ x2 + 4x + 4 < x + x2 - 3

    ⇔ (x2 - x2) + (4x - x) + 4 + 3 < 0

    ⇔ 3x + 7 < 0

    ⇔ x <73

    Vậy x < -73 .

    Bài 6: Hãy chọn câu đúng, x = -3 không là nghiệm của bất phương trình nào dưới đây?

    A. 2x + 1 > -5

    B. 7 - 2x ≤ 10 - x

    C. 3x - 2 ≤ 6 - 2x

    D. -3x > 4x + 3

    Đáp án: A

    Giải thích:

    Thay x = -3 vào từng bất phương trình ta được:

    Đáp án A: 2. (-3) + 1 = -5 > -5 (vô lí)

    nên x = -3 không là nghiệm của bất phương trình.

    Đáp án B: VT = 7 - 2. (-3) = 13, VP = 10 - (-3) = 13

    nên 13 ≤ 13 (đúng) nên x = -3 là nghiệm của bất phương trình.

    Đáp án C: VT = 3. (-3) - 2 = -11, VP = 6 - 2. (-3) = 12

    nên -11 ≤ 12 (đúng) nên x = -3 là nghiệm của bất phương trình.

    Đáp án D: VT = -3. (-3) = 9, VP = 4. (-3) + 3 = -9

    nên 9 > -9 (đúng) nên x = -3 là nghiệm của bất phương trình.

    Bài 7: Bất phương trình -x - 2 > 4, phép biến đổi nào sau đây là đúng?

    A. x < 4 - 2

    B. x < -4 + 2

    C. x < -4 - 2

    D. x > 4 + 2

    Đáp án: C

    Giải thích:

    Ta có: -x - 2 > 4, chuyển -2 từ vế trái sang vế phải

    ta được: -x > 4 + 2

    Nhân cả hai vế với -1 ta được: x < -4 - 2.

    Bài 8: Kết luận nào sau đây là đúng khi nói về nghiệm của bất phương trình (x + 3)(x + 4) > (x - 2)(x + 9) + 25?

    A. Bất phương trình vô nghiệm

    B. Bất phương trình vô số nghiệm x ∈ R

    C. Bất phương trình có tập nghiệm S = x>0

    D. Bất phương trình có tập nghiệm S = x<0

    Đáp án: B

    Giải thích:

    Ta có (x + 3)(x + 4) > (x - 2)(x + 9) + 25

    ⇔ x2 + 7x + 12 > x2 + 7x - 18 + 25

    ⇔ x2 + 7x + 12 - x2 - 7x + 18 - 25 > 0

    ⇔ 5 > 0

    Vì 5 > 0 (luôn đúng) nên bất phương trình có vô số nghiệm x ∈ R.

    Bài 9: Bất phương trình x - 2 < 1 tương đương với bất phương trình sau?

    A. x > 3

    B. x ≤ 3

    C. x - 1 > 2

    D. x - 1 < 2

    Đáp án: D

    Giải thích:

    Ta có x - 2 < 1

    ⇔ x - 2 + 1 < 1 + 1

    ⇔ x - 1 < 2

    Chuyển vế -2 từ vế trái sang vế phải thì phải đổi dấu ta được

    Bpt ⇔ x < 1 + 2

    ⇔ x < 3 nên loại đáp án A và B.

    Bài 10: Nghiệm của bất phương trình

    (x + 3) (x + 4) > (x - 2)(x + 9) + 25 là?

    A. x > 0

    B. Mọi x

    C. x < 0

    D. x < 1

    Đáp án: B

    Giải thích:

    Ta có: (x + 3)(x + 4) > (x - 2)(x + 9) + 25

    ⇔ x2 + 7x + 12 > x2 + 7x - 18 + 25

    ⇔ x2 + 7x + 12 - x2 - 7x + 18 - 25 > 0

    ⇔ 5 > 0

    Vì 5 > 0 (luôn đúng) nên bất phương trình vô số nghiệm x ∈ R.

    Xem thêm các bài tổng hợp lý thuyết Toán lớp 8 đầy đủ, chi tiết khác:

    Lý thuyết Bất phương trình bậc nhất một ẩn

    Lý thuyết Phương trình chứa dấu giá trị tuyệt đối

    Lý thuyết Ôn tập chương 4

    Lý thuyết Mở đầu về phương trình

    Lý thuyết Phương trình bậc nhất một ẩn và cách giải

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 5,452 25/02/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: