Lý thuyết Trường hợp đồng dạng thứ hai (mới 2023 + Bài Tập) – Toán 8
Lý thuyết Trường hợp đồng dạng thứ hai lớp 8 gồm lý thuyết chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm Toán 8 Bài 6: Trường hợp đồng dạng thứ hai.
Lý thuyết Toán 8 Bài 6: Trường hợp đồng dạng thứ hai
Bài giảng Toán 8 Bài 6: Trường hợp đồng dạng thứ hai
A. Lý thuyết
1. Định lí
- Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng
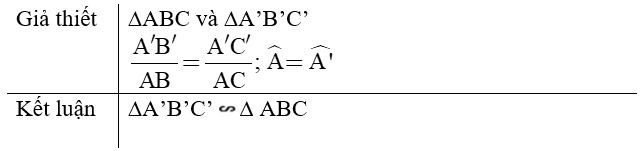
- Ví dụ 1. Cho tam giác ABC có AB = 15cm; AC = 20cm. Trên hai cạnh AB, AC lần lượt lấy 2 điểm E, D sao cho AD = 8cm; AE = 6cm.
Chứng minh ∆AED∆ ABC.
Lời giải:
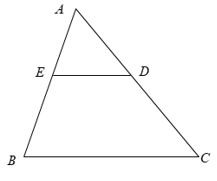
Xét ∆AED và ∆ABC có:
Suy ra: ∆AED∆ ABC (c – g – c).
B. Bài tập tự luyện
Bài 1. Cho góc . Trên tia Ox lấy 2 điểm A và C sao cho OA = 4cm; OC = 10cm. Trên tia Oy lấy hai điểm B và D sao cho OB = 5cm; OD = 8cm
Chứng minh ∆OBC∆OAD.
Lời giải:
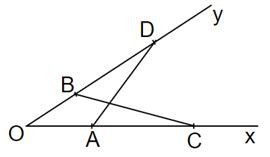
Xét ∆OBC và ∆ OAD có:
chung.
Suy ra: ∆OBC ∆ OAD (c – g – c) (đpcm).
Bài 2. Cho tam giác ABC có AC = 12cm; BC = 8cm. Trên cạnh AC lấy điểm E sao cho AE = 7cm. Trên cạnh BC lấy điểm D sao cho DC = 4,5. Chứng minh; .
Lời giải:
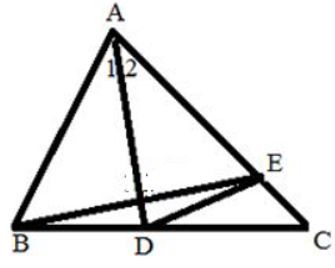
Ta có: CE = AC – AE = 10 – 7 = 3cm
Xét ∆CED và ∆ CBA có:
chung.
Suy ra: ∆CED∆CBA (c.g.c)
Do đó: (2 góc tương ứng) (đpcm).
Bài 3. Chỉ ra các tam giác đồng dạng với nhau trong hình vẽ sau?
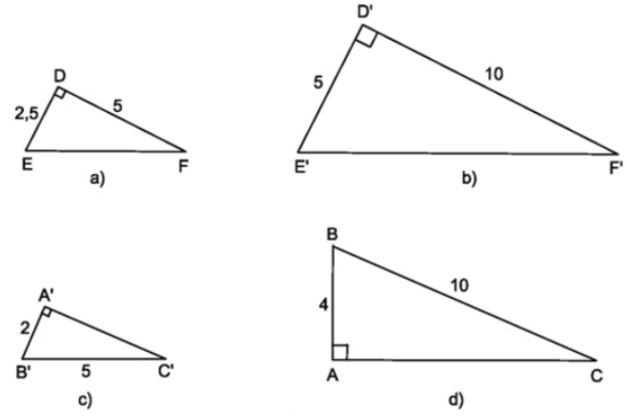Lời giải:
+ Xét ∆DEF và ∆ D’E’F’ có:
Suy ra: ∆DEF∆D’E’F’.
+ Áp dụng định lí py tago ta có:
Xét ∆ABC và ∆ A’B’C’ có:
Suy ra: ∆ABC∆A’B’C’.
Trắc nghiệm Toán 8 Bài 6: Trường hợp đồng dạng thứ hai của tam giác
Bài 1: Để hai tam giác ABC và EDF đồng dạng thì số đo góc D trong hình vẽ dưới bằng:
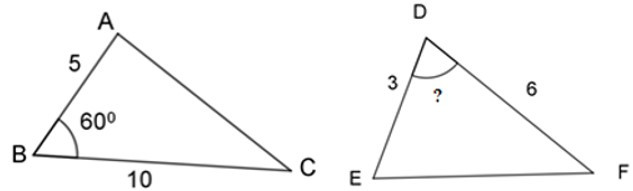
A. 500
B. 600
C. 300
D. 700
Đáp án: B
Giải thích:
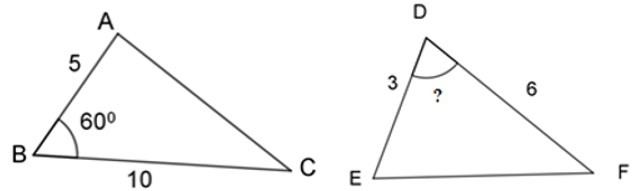
Có:
Để hai tam giác đã cho đồng dạng thì góc ABC = EDF = 600.
Bài 2: Với AB // CD thì giá trị của x trong hình vẽ dưới đây là
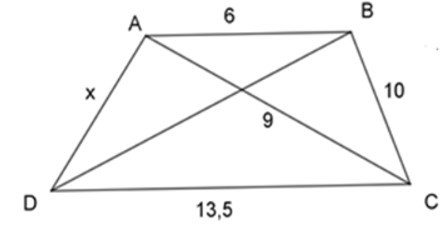
A. x = 15
B. x = 16
C. x = 7
D. x = 8
Đáp án: A
Giải thích:
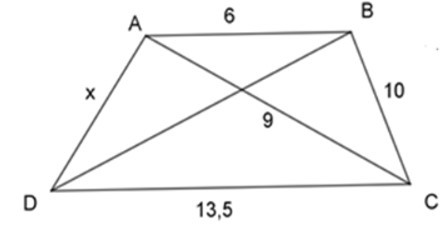
Ta có:
Bài 3: Cho hình vẽ dưới đây, tính giá trị của x?
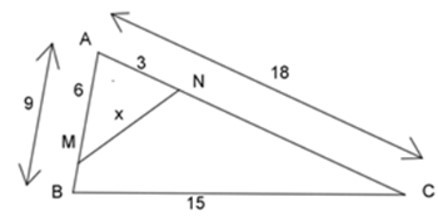
A. x = 6
B. x = 5
C. x = 8
D. x = 9
Đáp án: B
Giải thích:
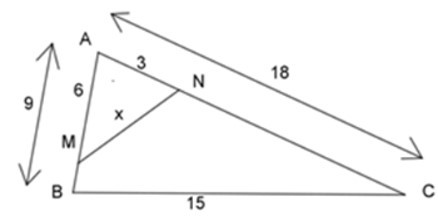
Ta có:
Bài 4: Cho tam giác ABC có AB = 8cm, AC = 16cm.
Điểm D thuộc cạnh AB sao cho BD = 2cm.
Điểm E thuộc cạnh AC sao cho CE = 13cm.
1. Chọn câu đúng.
A. ΔEDA ~ ΔABC
B. ΔADE ~ ΔABC
C. ΔAED ~ ΔABC
D. ΔDEA ~ ΔABC
Đáp án: C
Giải thích:
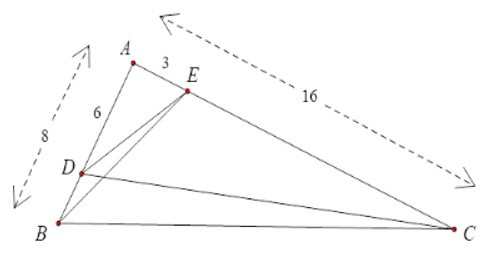
Ta có:
Xét ΔAED và ΔABC có A chung
và (cmt)
Nên ΔAED ~ ΔABC (c.g.c)
2. Chọn câu sai.
A.
B. AE.CD = AD. BC
C. AE.CD = AD.BE
D. AE.AC = AD.AB
Đáp án: B
Giải thích:
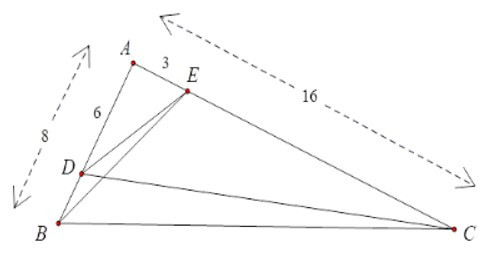
+ Xét ΔABE và ΔACD có A chung
và nên
ΔABE ~ ΔACD (c - g - c)
suy ra góc (hai góc tương ứng)
và
=> AE.CD = AD.BE
+ ΔAED ~ ΔABC (cmt)
nên
AE.AC = AB.AD
Nên A, C, D đúng, B sai.
Bài 5: Cho tam giác ABC có AB = 12cm, AC = 18cm, BC = 27cm. Điểm D thuộc cạnh BC sao cho CD = 12cm. Tính độ dài AD.
A. 12cm
B. 6cm
C. 10cm
D. 8cm
Đáp án: D
Giải thích:
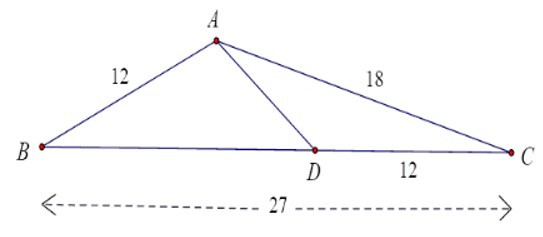
Ta có
Bài 6: Cho tam giác nhọn ABC có C = 400. Vẽ hình bình hành ABCD. Gọi AH, AK theo thứ tự là các đường cao của các tam giác ABC, ACD. Tính số đo góc AKH.
A. 300
B. 400
C. 450
D. 500
Đáp án: B
Giải thích:
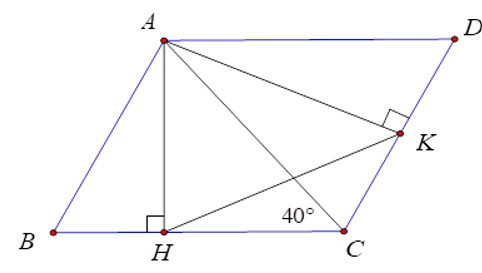
Vì AD.AH = AB.AK (=SABCD)
Bài 7: Cho hình vẽ dưới đây, tính giá trị của x?
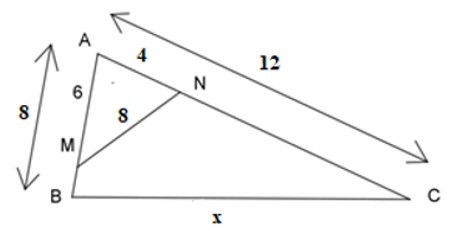
A. x = 4
B. x = 16
C. x = 10
D. x = 14
Đáp án: B
Giải thích:
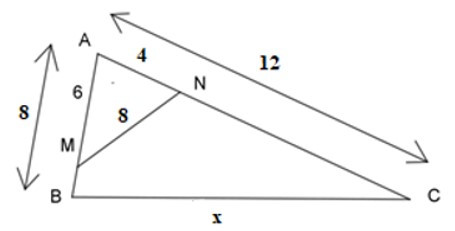
Ta có:
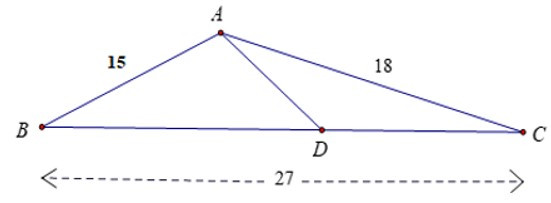
Bài 8: Cho tam giác ABC có AB = 15cm, AC = 18cm, BC = 27cm. Điểm D
thuộc cạnh BC sao cho . Độ dài AD là:
A. 12cm
B. 6cm
C. 10cm
D. 8cm
Đáp án: C
Giải thích:
Bài 9: Cho hình thang vuông ABCD (A = D = 900) có AB = 16cm, CD = 25cm, BD = 20cm.
1. Tam giác ABD đồng dạng với tam giác nào dưới đây?
A. ΔBDC
B. ΔCBD
C. ΔBCD
D. ΔDCB
Đáp án: A
Giải thích:
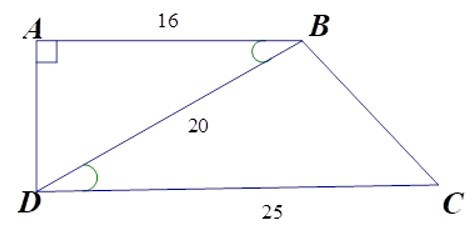
ΔABD và ΔBDC có góc ABD = BDC (hai góc ở vị trí so le trong bằng nhau do AB // CD);
Và (vì )
Do đó ΔABD ~ ΔBDC (c.g.c)
2. Độ dài cạnh BC là
A. 10cm
B. 12cm
C. 15cm
D. 9cm
Đáp án: C
Giải thích:
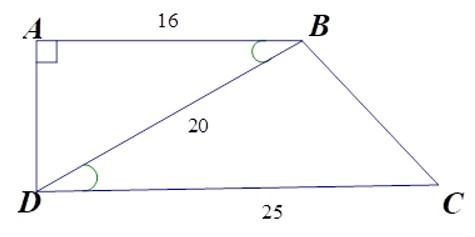
Vì ΔABD ~ ΔBDC (cmt) nên góc A = DBC.
Ta có A = 900 nên DBC = 900. Theo định lí Pytago, ta có
BC2 = CD2 - BD2 = 252 - 202 = 152.
Vậy BC = 15cm
Bài 10: Cho hình thang ABCD có: AB // CD, AB = 4, CD = 16, AC = 8, AD = 12. Độ dài BC là:
A. 8
B. 13
C. 12
D. 6
Đáp án: D
Giải thích:
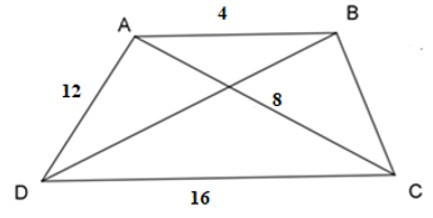
Ta có:
Xem thêm các bài tổng hợp lý thuyết Toán lớp 8 đầy đủ, chi tiết khác:
Lý thuyết Trường hợp đồng dạng thứ ba
Xem thêm các chương trình khác:
- Tóm tắt tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 8 (hay nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Soạn văn 8 (ngắn nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Văn mẫu lớp 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Hóa học 8
- Giải sbt Hóa học 8
- Giải vở bài tập Hóa học 8
- Lý thuyết Hóa học 8
- Các dạng bài tập Hóa học lớp 8
- Giải sgk Vật Lí 8
- Giải sbt Vật Lí 8
- Lý thuyết Vật Lí 8
- Giải vở bài tập Vật lí 8
- Giải sgk Tiếng Anh 8 (sách mới) | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2
- Giải sgk Tiếng Anh 8 | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2 (sách mới)
- Giải sbt Tiếng Anh 8 (sách mới) | Sách bài tập Tiếng Anh 8
- Giải sbt Tiếng Anh 8 (thí điểm)
- Giải sgk Tin học 8 | Giải bài tập Tin học 8 Học kì 1, Học kì 2 (sách mới)
- Giải sgk Lịch Sử 8 | Giải bài tập Lịch sử 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Lịch sử 8 (sách mới) | Kiến thức trọng tâm Lịch sử 8
- Giải vở bài tập Lịch sử 8
- Giải Tập bản đồ Lịch sử 8
- Đề thi Lịch Sử 8
- Giải vở bài tập Sinh học 8
- Giải sgk Sinh học 8
- Lý thuyết Sinh học 8
- Giải sgk Giáo dục công dân 8 | Giải bài tập Giáo dục công dân 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Giáo dục công dân 8 (sách mới) | Kiến thức trọng tâm GDCD 8
- Lý thuyết Địa Lí 8 (sách mới) | Kiến thức trọng tâm Địa Lí 8
- Giải sgk Địa Lí 8 | Giải bài tập Địa Lí 8 Học kì 1, Học kì 2 (sách mới)
- Giải Tập bản đồ Địa Lí 8
- Đề thi Địa lí 8