Lý thuyết Chia đa thức một biến đã sắp xếp (mới 2023 + Bài Tập) – Toán 8
Lý thuyết Chia đa thức một biến đã sắp xếp lớp 8 gồm lý thuyết chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm Toán 8 Bài 12: Chia đa thức một biến đã sắp xếp.
Lý thuyết Toán 8 Bài 12: Chia đa thức một biến đã sắp xếp
Bài giảng Toán 8 Bài 12: Chia đa thức một biến đã sắp xếp
A. Lý thuyết
1. Phép chia hết
- Phép chia hết là phép chia có đa thức dư bằng 0.
Quy tắc chia:
+ Sắp xếp các đa thức theo thứ tự giảm dần của biến.
+ Lấy hạng tử cao nhất của đa thức bị chia chia cho hạng tử cao nhất của đa thức chia ta được thương 1.
+ Nhân thương 1 với đa thức chia và lấy đa thức bị chia trừ đi tích đó.
+ Lấy hạng tử cao nhất của đa thức vừa tìm được chia cho hạng tử cao nhất đa thức chia ta được thương 2.
+ Tiếp tục lặp lại các bước trên đến khi nhận được hiệu bằng 0.
Ví dụ 1: Làm tính chia: (x3 – x2 – 5x – 3) : (x – 3).
Lời giải:
Ta có:
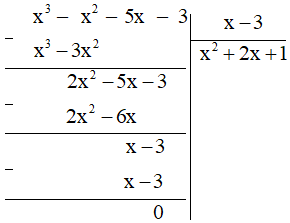
Vậy (x3 – x2 – 5x – 3) : (x – 3) = x2 + 2x + 1.
2. Phép chia có dư
- Phép chia có dư là phép chia có đa thức dư khác 0.
Quy tắc chia: Làm tương tự phép chia hết đến khi thu được đa thức dư có bậc nhỏ hơn bậc của đa thức chia.
Chú ý: Với hai đa thức tùy ý A và B của cùng một biến (B ≠ 0), tồn tại duy nhất một cặp đa thức Q và R sao cho A = B.Q + R, trong đó R = 0 hoặc bậc của R nhỏ hơn bậc của B (R được gọi là dư trong phép chia A cho B).
Khi R = 0 phép chia A cho B là phép chia hết.
Ví dụ 2: Làm tính chia: (3x3 + 2x2 + 5x – 3) : (x2 + 1).
Lời giải:
Ta có:
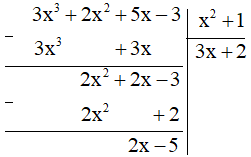
Vậy (3x3 + 2x2 + 5x – 3) : (x2 + 1) = 3x + 2 (dư 2x – 5)
Hay 3x3 + 2x2 + 5x – 3 = (x2 + 1).(3x + 2) + 2x – 5.
B. Bài tập tự luyện
Bài 1: Sắp xếp các đa thức theo thũy thừa giảm dần của biến rồi làm phép chia:
a) (5x2 + 15 – 3x3 – 9x) : (5 – 3x);
b) (x3 + 5x + x2 – 1) : (x – 1);
c) (12x – 3x2 + 2x3 – 13) : (x2 + 4).
Lời giải:
a) Sắp xếp đa thức bị chia và đa thức chia theo thứ tự giảm dần của biến ta được:
– 3x3 + 5x2 – 9x + 15 và – 3x + 5.
Thực hiện phép chia:
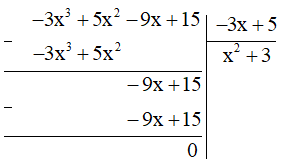
Vậy (5x2 + 15 – 3x3 – 9x) : (5 – 3x) = x2 + 3.
b) Sắp xếp đa thức ta được: x3 + x2 + 5x – 1.
Thực hiện phép:
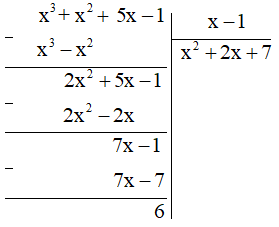
Vậy x3 + 5x + x2 – 1 = (x – 1)(x2 + 2x + 7) + 6.
c) Sắp xếp đa thức ta được: 2x3 – 3x2 + 12x – 13.
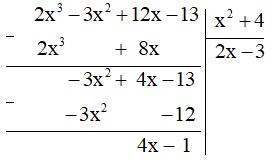
Vậy 12x – 3x2 + 2x3 – 13 = (x2 + 4).(2x – 3) + 4x – 1.
Bài 2: Áp dụng các hằng đẳng thức đáng nhớ để thực hiện phép chia:
a) (8x3 + 27) : (2x + 3);
b) (a3 + 6a2 + 12a + 8) : (a + 2);
c) (m3 – 9 m2n + 27mn2 – 27n3) : (m – 3n)2.
Lời giải:
a) (8x3 + 27) : (2x + 3)
= (2x + 3)(4x2 – 6x + 9) : (2x + 3)
= 4x2 – 6x + 9.
b) (a3 + 6a2 + 12a + 8) : (a + 2)
= (a + 2)3 : (a + 2)
= (a + 2)2
c) (m3 – 9 m2n + 27mn2 – 27n3) : (m – 3n)2
= (m – 3n)3 : (m – 3n)2
= m – 3n .
Bài 3: Tìm đa thức M biết:
2x6 – x4 – 2x2 + 1 = M. (2x2 – 1).
Lời giải:
a) Ta có: 2x6 – x4 – 2x2 + 1 = M. (2x2 – 1)
Suy ra M = (2x6 – x4 – 2x2 + 1) : (2x2 – 1)
Thực hiện phép chia:
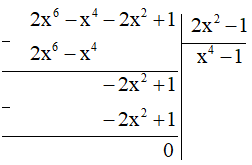
Vậy M = x4 – 1.
Bài 4: Tìm a để đa thức A chia hết cho đa thức B với:
A = x3 – 6x2 + 11x + a và B = x2 – 2x + 3.
Lời giải:
Thực hiện phép chia A cho B ta được:
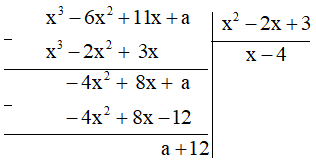
Để đa thức A chia hết cho đa thức B thì a + 12 = 0. Suy ra a = – 12.
Vậy a = – 12 thì đa thức A chia hết cho đa thức B.
Trắc nghiệm Toán 8 Bài 12: Chia đa thức cho một biến đã sắp xếp
Bài 1: Phép chia đa thức 2x4 – 3x3 + 3x – 2
cho đa thức x2 – 1 được đa thức dư là
A. 0
B. 1
C. 2
D. 10
Đáp án: A
Giải thích:
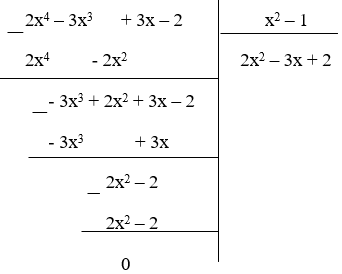
Vậy đa thức dư là R = 0
Bài 2: Cho các khẳng định sau:
(I): Phép chia đa thức 3x3 – 2x2 + 5 cho đa thức 3x – 2 là phép chia hết
(II): Phép chia đa thức (2x3 + 5x2 – 2x + 3) cho đa thức (2x2 – x + 1) là phép chia hết
Chọn câu đúng
A. Cả (I) và (II) đều đúng
B. Cả (I) và (II) đều sai
C. (I) đúng, (II) sai
D. (I) sai, (II) đúng
Đáp án: D
Giải thích:
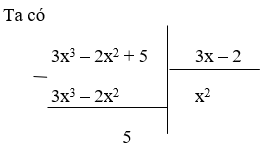
Vì phần dư R = 5 ≠ 0 nên phép chia đa thức 3x3 – 2x2 + 5 cho đa thức 3x – 2 là phép chia có dư.
Do đó (I) sai
Lại có
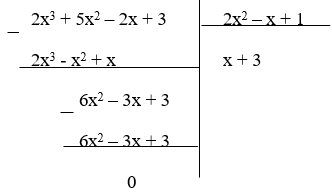
Nhận thấy phần dư R = 0 nên phép chia đa thức (2x3 + 5x2 – 2x + 3) cho đa thức (2x2 – x + 1) là phép chia hết.
Do đó (II) đúng
Bài 3: Phép chia đa thức (4x4 + 3x2 – 2x + 1) cho đa thức x2 + 1 được đa thức dư là:
A. 2x + 2
B. -2x + 2
C. -2x - 2
D. 3 - 2x
Đáp án: B
Giải thích:
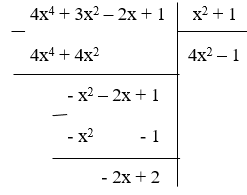
Vậy đa thức dư là R = -2x + 2
Bài 4: Phép chia đa thức 3x5 + 5x4 – 1
cho đa thức x2 + x + 1 được đa thức thương là:
A. 3x3 – 2x2 – 5x + 3
B. 3x3 + 2x2 – 5x + 3
C. 3x3 – 2x2 – x + 3
D. 2x – 4
Đáp án: B
Giải thích:
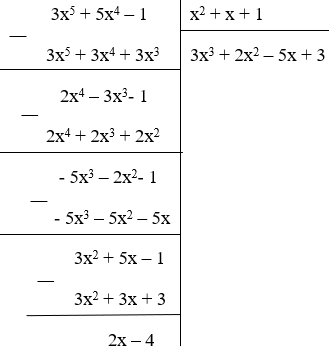
Đa thức thương là: 3x3 + 2x2 – 5x + 3
Bài 5: Cho các khẳng định sau:
(I): Phép chia đa thức (2x3 – 26x – 24) cho đa thức x2 + 4x + 3 là phép chia hết
(II): Phép chia đa thức (x3 – 7x + 6) cho đa thức x + 3 là phép chia hết
Chọn câu đúng
A. Cả (I) và (II) đều đúng
B. Cả (I) và (II) đều sai
C. (I) đúng, (II) sai
D. (I) sai, (II) đúng
Đáp án: A
Giải thích:
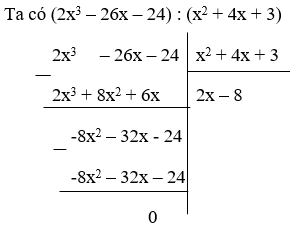
Vì phần dư R = 0 nên Phép chia đa thức(2x3 – 26x – 24) cho đa thức x2 + 4x + 3 là phép chia hết.
Do đó (I) đúng.
Lại có
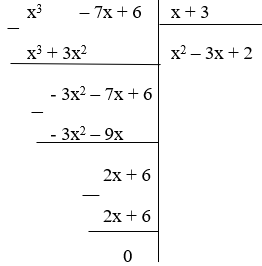
Nhận thấy phần dư R = 0 nên phép chia đa thức (x3 – 7x + 6) cho đa thức x + 3 là phép chia hết.
Do đó (II) đúng
Bài 6: Điền vào chỗ trống (x3 + x2 – 12) : (x – 12) = …
A. x + 3
B. x – 3
C. x2 + 3x + 6
D. x2 – 3x + 6
Đáp án: C
Giải thích:
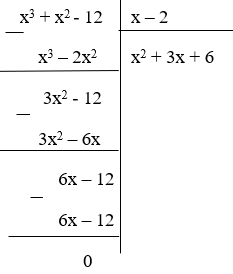
Vậy đa thức cần điền vào chỗ trống là x2 + 3x + 6
Bài 7: Kết quả của phép chia
(2a3 + 7ab2 – 7a2b – 2b3) : (2a – b) là
A. (a – b)(a – 2b)
B. (a + b)2
C. (a – b)(b – 2a)
D. a – b
Đáp án: A
Giải thích:
Ta có 2a3 + 7ab2 – 7a2b – 2b3
= 2(a3 – b3) – 7ab(a – b)
= 2(a – b)(a2 + ab + b2) – 7ab(a – b)
= (a – b)(2a2 – ab – 4ab + 2b2)
= (a – b)[a(2a – b) – 2b(2a – b)]
= (a – b)(2a – b)(a – 2b)
Nên (2a3 + 7ab2 – 7a2 – 2b3) : (2a – b)
= (a – b)(2a – b)(a – 2b) : (2a – b)
= (a – b)(a – 2b)
Bài 8: Phần dư của phép chia đa thức
x4 – 2x3 + x2 – 3x + 1 cho đa thức x2 + 1 có hệ số tự do là
A. 2
B. 3
C. 1
D. 4
Đáp án: C
Giải thích:
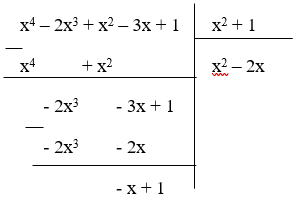
Đa thức dư là – x + 1 có hệ số tự do là 1.
Bài 9: Xác định a để đa thức
10x2 – 7x + a chia hết cho 2x – 3
A. a = 24
B. a = 12
C. a = -12
D. a = 9
Đáp án: C
Giải thích:
(10x2 – 7x + a) ⁝ (2x – 3)
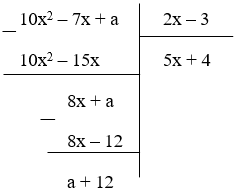
Để 10x2 – 7x + a chia hết cho 2x – 3
thì a + 12 = 0 a = -12
Bài 10: Thương của phép chia đa thức
(3x4 – 2x3 + 4x – 2x2 – 8) cho đa thức (x2 – 2) có hệ số tự do là
A. 2
B. 3
C. 1
D. 4
Đáp án: D
Giải thích:
Ta có:
(3x4 – 2x3 + 4x – 2x2 – 8) : (x2 – 2)
= (3x4 – 2x3– 2x2 + 4x – 8) : (x2 – 2)
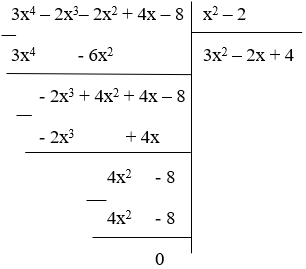
(3x4 – 2x3– 2x2 + 4x – 8) : (x2 – 2) = 3x2 – 2x + 4
Hệ số tự do của thương là 4
Xem thêm các bài tổng hợp lý thuyết Toán lớp 8 đầy đủ, chi tiết khác:
Lý thuyết Phân tích đa thức thành nhân tử bằng phương pháp nhóm các hạng tử
Lý thuyết Phân tích đa thức thành nhân tử bằng các phối hợp nhiều phương pháp
Lý thuyết Chia đơn thức cho đơn thức
Xem thêm các chương trình khác:
- Tóm tắt tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 8 (hay nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Soạn văn 8 (ngắn nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Văn mẫu lớp 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Hóa học 8
- Giải sbt Hóa học 8
- Giải vở bài tập Hóa học 8
- Lý thuyết Hóa học 8
- Các dạng bài tập Hóa học lớp 8
- Giải sgk Vật Lí 8
- Giải sbt Vật Lí 8
- Lý thuyết Vật Lí 8
- Giải vở bài tập Vật lí 8
- Giải sgk Tiếng Anh 8 (sách mới) | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2
- Giải sgk Tiếng Anh 8 | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2 (sách mới)
- Giải sbt Tiếng Anh 8 (sách mới) | Sách bài tập Tiếng Anh 8
- Giải sbt Tiếng Anh 8 (thí điểm)
- Giải sgk Tin học 8 | Giải bài tập Tin học 8 Học kì 1, Học kì 2 (sách mới)
- Giải sgk Lịch Sử 8 | Giải bài tập Lịch sử 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Lịch sử 8 (sách mới) | Kiến thức trọng tâm Lịch sử 8
- Giải vở bài tập Lịch sử 8
- Giải Tập bản đồ Lịch sử 8
- Đề thi Lịch Sử 8
- Giải vở bài tập Sinh học 8
- Giải sgk Sinh học 8
- Lý thuyết Sinh học 8
- Giải sgk Giáo dục công dân 8 | Giải bài tập Giáo dục công dân 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Giáo dục công dân 8 (sách mới) | Kiến thức trọng tâm GDCD 8
- Lý thuyết Địa Lí 8 (sách mới) | Kiến thức trọng tâm Địa Lí 8
- Giải sgk Địa Lí 8 | Giải bài tập Địa Lí 8 Học kì 1, Học kì 2 (sách mới)
- Giải Tập bản đồ Địa Lí 8
- Đề thi Địa lí 8
