Nội dung bài viết

    Xem thêm

    Lý thuyết Phương trình tích (mới 2023 + Bài Tập) – Toán 8

    Lý thuyết Phương trình tích lớp 8 gồm lý thuyết chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm Toán 8 Bài 4: Phương trình tích.

    1 8,155 25/02/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Lý thuyết Toán 8 Bài 4: Phương trình tích

    Bài giảng Toán 8 Bài 4: Phương trình tích

    A. Lý thuyết

    Phương trình tích có dạng A(x)B(x) = 0.

    Ví dụ 1. (2x + 3)(1 – x) là phương trình tích.

    Cách giải phương trình tích A(x)B(x) = 0⇔A(x)=0B(x)=0

    Cách bước giải phương trình tích

    Bước 1: Đưa phương trình đã cho về dạng tổng quát A(x)B(x) = 0 bằng cách:

    + Chuyển tất cả các hạng tử của phương trình về vế trái. Khi đó vế phải bằng 0.

    + Phân tích đa thức ở vế phải thành nhân tử.

    Bước 2: Giải phương trình và kết luận.

    Ví dụ 2. Giải phương trình: (x + 1)(2x – 3) = 0.

    Lời giải:

    (x + 1)(2x – 3) = 0

    ⇔x + 1 = 0 hoặc 2x – 3 = 0.

    + x + 1 = 0⇔x = –1;

    + 2x – 3 = 0⇔2x = 3⇔x=32.

    Vậy tập nghiệm của phương trình đã cho là S=-1; 32.

    Ví dụ 3. Giải phương trình: 2x3 + 3x2 = 4x2 + 6x.

    Lời giải:

    2x3 + 3x2 = 4x2 + 6x

    ⇔(2x3 + 3x2) – (4x2 + 6x) = 0

    ⇔2x2(2x + 3) – 4x(2x + 3) = 0

    ⇔(2x2 – 4x) (2x + 3) = 0

    ⇔2x(x – 2) (2x + 3) = 0

    ⇔2x = 0 hoặc x – 2 = 0 hoặc 2x + 3 = 0.

    + 2x = 0⇔x = 0;

    + x – 2 = 0⇔x = 2;

    + 2x + 3 = 0⇔2x = – 3 .

    Vậy tập nghiệm của phương trình là S=0; 2; -32.

    B. Bài tập tự luyện

    Bài 1. Giải phương trình: (x – 7)(3x + 5) = 0.

    Lời giải:

    (x – 7)(3x + 5) = 0

    ⇔x – 7 = 0 hoặc 3x + 5 = 0.

    + x – 7 = 0⇔x = 7;

    + 3x + 5 = 0⇔3x = – 5⇔x=-53.

    Vậy tập nghiệm của phương trình đã cho là S=7; -53.

    Bài 2. Giải phương trình: x2 + x – (2x + 2) = 0.

    Lời giải:

    x2 + x – (2x + 2) = 0

    ⇔x(x + 1) – 2(x + 1) = 0

    ⇔(x + 1)(x – 2) = 0

    ⇔x + 1 = 0 hoặc x – 2 = 0.

    + x + 1 = 0⇔x = – 1;

    + x – 2 = 0⇔x = 2.

    Vậy tập nghiệm của phương trình đã cho là S = {– 1; 2}.

    Bài 3. Giải phương trình: (2x + 1)(x – 2) = (x + 3)(2 – x).

    Lời giải:

    (2x + 1)(x – 2) = (x + 3)(2 – x)

    ⇔(2x + 1)(x – 2) – (x + 3)(2 – x) = 0

    ⇔(2x + 1)(x – 2) + (x + 3)( x – 2) = 0

    ⇔(x – 2) (2x + 1 + x + 3) = 0

    ⇔(x – 2) (3x + 4) = 0

     ⇔x – 2 = 0 hoặc 3x + 4 = 0.

    + x – 2 = 0⇔x = 2;

    + 3x + 4 = 0⇔3x = – 4 .

    Vậy tập nghiệm của phương trình đã cho là S = 2; -43.

    Trắc nghiệm Toán 8 Bài 4: Phương trình tích

    Bài 1: Các nghiệm của phương trình (2 - 6x)(-x2 – 4) = 0 là

    A. x = 3

    B. x =-13

    C. x = -3

    D.x = 13

    Đáp án: D

    Giải thích:

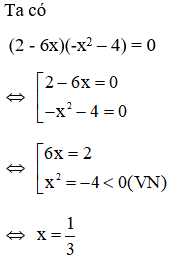
    Trắc nghiệm Phương trình tích có đáp án - Toán lớp 8 (ảnh 1)

    Phương trình có ngiệm duy nhất x =13

    Bài 2: Tổng các nghiệm của phương trình

    (x2 – 4)(x + 6)(x – 8) = 0 là:

    A. 1

    B. 2

    C. 3

    D. 4

    Đáp án: B

    Giải thích:

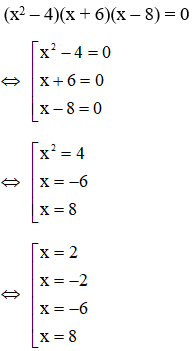
    Trắc nghiệm Phương trình tích có đáp án - Toán lớp 8 (ảnh 1)

    Tổng các nghiệm của phương trình

    là 2 + (-2) + (-6) + 8 = 2

    Bài 3: Phương trình (x2 – 1)(x – 2)(x – 3) = 0

    có số nghiệm là:

    A. 1

    B. 2

    C. 3

    D. 4

    Đáp án: D

    Giải thích:

    Ta có (x2 – 1)(x – 2)(x – 3) = 0

    ⇔x2−1=0x−2=0x−3=0

    ⇔x=±1x=2x=3 

    Vậy phương trình có

    bốn nghiệm x = -1; x = 1, x = 2, x = 3

    Bài 4: Tìm m để phương trình (2m – 5)x – 2m2 – 7 = 0

    nhận x = -3 làm nghiệm

    A. m = 1 hoặc m = 4

    B. m = -1 hoặc m = -4

    C. m = -1 hoặc m = 4

    D. m = 1 hoặc m = -4

    Đáp án: D

    Giải thích:

    Thay x = -3 vào phương trình

    (2m – 5)x – 2m2 – 7 = 0 ta được

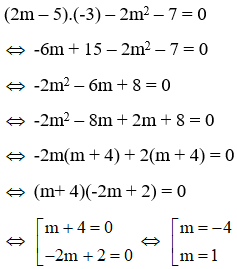
    Trắc nghiệm Phương trình tích có đáp án - Toán lớp 8 (ảnh 1)

    Vậy m = 1 hoặc m = -4

    thì phương trình có nghiệm x = -3

    Bài 5: Tập nghiệm của phương trình (2x + 1)(2 - 3x) = 0 là:

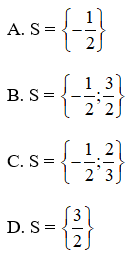
    Trắc nghiệm Phương trình tích có đáp án - Toán lớp 8 (ảnh 1)

    Đáp án: C

    Giải thích:

    Ta có (2x + 1)(2 - 3x) = 0

    ⇔2x+1=02−3x=0⇔x=−12x=23

    Vậy tập nghiệm của phương trình đã cho là

     S =−12;23 .

    Bài 6: Tổng các nghiệm của phương trình

    (x2 + 4)(x + 6)(x2 – 16) = 0 là:

    A. 16

    B. 6

    C. -10

    D. -6

    Đáp án: D

    Giải thích:

    Ta có (x2 + 4)(x + 6)(x2 – 16) = 0

    ⇔x2+4=0x+6=0x2−16=0

    ⇔x2=−4(VN)x=−6x2=16

    ⇔x2=−4(VN)x=−6x=±4

    Tổng các nghiệm của phương trình

    là: -6 + (-4) + 4 = -6

    Bài 7: Số nghiệm của phương trình

    2x2+3x+4=x2+x+4 là

    A. 0

    B. 1

    C. 2

    D. 3

    Đáp án: C

    Giải thích:

    Trắc nghiệm Phương trình tích có đáp án - Toán lớp 8 (ảnh 1)

    Bài 8: Tập nghiệm của phương trình

    (5x2 – 2x + 10)2 = (3x2 +10x – 8)2 là:

    A. S = {12; 3}

    B. S = {12; -3}

    C. S = {-12 ; 3}

    D. S = {-12 ; -3}

    Đáp án: C

    Giải thích:

    (5x2 – 2x + 10)2 = (3x2 +10x – 8)2

     ⇔(5x2 – 2x + 10)2 - (3x2 +10x – 8)2 = 0

     ⇔(5x2 – 2x + 10 + 3x2 +10x – 8)(5x2 – 2x + 10 – 3x2 – 10x + 8) = 0

     ⇔(8x2 + 8x + 2)(2x2 – 12x + 18) = 0

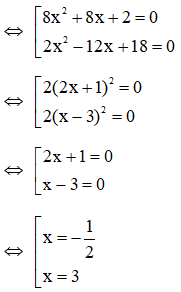
    Trắc nghiệm Phương trình tích có đáp án - Toán lớp 8 (ảnh 1)

    Vậy phương trình có tập nghiệm: S = {-12; 3}

    Bài 9: Tìm m để phương trình

    (2m – 5)x – 2m2 + 8 = 43 có nghiệm x = -7

    A. m = 0 hoặc m = 7

    B. m = 1 hoặc m = -7

    C. m = 0 hoặc m = -7

    D. m = -7

    Đáp án: C

    Giải thích:

    Thay x = -7 vào phương trình (2m – 5)x – 2m2 + 8 = 43 ta được:

    (2m – 5)(-7) – 2m2 + 8 = 43

    ⇔-14m + 35 – 2m2 – 35 = 0

    ⇔2m2 + 14m = 0

    ⇔2m(m + 7) = 0

    ⇔m=0m+7=0

    ⇔m=0m=−7

    Vậy m = 0 hoặc m = -7

    thì phương trình có nghiệm x = -7

    Bài 10: Số nghiệm của phương trình

    (5x2 – 2x + 10)3 = (3x2 +10x – 6)3 là:

    A. 1

    B. 2

    C. 3

    D. 0

    Đáp án: B

    Giải thích:

    (5x2 – 2x + 10)3 = (3x2 +10x – 6)3

    ⇔5x2 – 2x + 10 = 3x2 +10x – 6

    ⇔5x2 – 3x2 – 2x – 10x + 10 + 6 = 0

    ⇔2x2 – 12x + 16 = 0

    ⇔x2 – 6x + 8 = 0

    ⇔x2 – 4x – 2x + 8 = 0

    ⇔x(x – 4) – 2(x – 4) = 0

    ⇔(x – 2)(x – 4) = 0

    ⇔x−2=0x−4=0

    ⇔x=2x=4

    Vậy phương trình có 2 nghiệm

    Xem thêm các bài tổng hợp lý thuyết Toán lớp 8 đầy đủ, chi tiết khác:

    Lý thuyết Phương trình chứa ẩn ở mẫu

    Lý thuyết Giải bài toán bằng cách lập phương trình

    Lý thuyết Ôn tập chương 3

    Lý thuyết Liên hệ giữa thứ tự và phép cộng

    Lý thuyết Liên hệ giữa thứ tự và phép nhân

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 8,155 25/02/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: