SBT Toán 8 Ôn tập chương 4

Mục lục Giải SBT Toán 8 Ôn tập chương 4

Bài 71 trang 61 SBT Toán 8 Tập 2: Cho các bất đẳng thức:

a > b; a < b; c > 0; c < 0; a + c < b + c;

a + c > b + c; ac < bc; ac > bc

Hãy điền các bất đẳng thức thích hợp vào chỗ trống (...) trong câu sau: 

Nếu……… và………. thì………..

Lời giải:

Nếu a > b và c > 0 thì ac > bc

Nếu a > b và c > 0 thì a + c > b + c

Nếu a > b và c < 0 thì a + c > b + c

Nếu a > b và c < 0 thì ac < bc

Nếu a < b và c > 0 thì ac < bc

Nếu a < b và c > 0 thì a + c < b + c

Nếu a < b và c < 0 thì ac > bc

Nếu a < b và c < 0 thì a + c < b + c

Bài 72 trang 61 SBT Toán 8 Tập 2: Cho a > b, chứng tỏ:

a) 3a + 5 > 3b + 2;

b) 2 – 4a < 3 – 4b.

Lời giải:

a) Ta có: a > b ⇔ 3a > 3b

⇔ 3a + 5 > 3b + 5 (1)

Mặt khác: vì 5 > 2

nên 3b + 5 > 3b + 2 (2)

Từ (1) và (2) suy ra: 3a + 5 > 3b + 2

( điều phải chứng minh).

b) Ta có: a > b ⇔ –4a < –4b

⇔ 3 – 4a < 3 – 4b (1)

Mặt khác: 2 < 3 nên 2 – 4a < 3 – 4a (2)

Từ (1) và (2) suy ra: 2 – 4a < 3 – 4b

(điều phải chứng minh).

Bài 73 trang 61 SBT Toán 8 Tập 2:

a) Chứng tỏ 2,99 là nghiệm của bất phương trình 3 > x. Hãy kể ra bốn số lớn hơn 2,99 là nghiệm của bất phương trình đó.

b) Chứng tỏ 4,01 là nghiệm của bất phương trình 4 < x. Hãy kể ra ba số nhỏ hơn 4,01 là nghiệm của bất phương trình đó.

Lời giải:

a) Ta có 2,99 là nghiệm của bất phương trình 3 > x vì 3 > 2,99.

Bốn số lớn hơn 2,99 là nghiệm của bất phương trình là: 2,999; 2,998; 2,997; 2,996.

b) Ta có 4,01 là nghiệm của bất phương trình 4 < x vì 4 < 4,01. Ba số nhỏ hơn 4,01 là nghiệm của bất phương trình là: 4,003; 4,002; 4,001.

Bài 74 trang 61 SBT Toán 8 Tập 2: Giải các bất phương trình và biểu diễn tập nghiệm của chúng trên trục số.

a) 2(3x – 1) – 2x < 2x + 1;

b) 4x – 8 ≥ 3(3x – 2) + 4 – 2x.

Lời giải:

a) Ta có: 2(3x – 1) – 2x < 2x + 1

 ⇔ 6x – 2 – 2x < 2x + 1

 ⇔ 6x – 2x – 2x < 1 + 2

 ⇔ 2x < 3

 ⇔ $x\text{\hspace{0.17em}}<\frac{3}{2}$

Vậy tập nghiệm của bất phương trình là

S = {x| $x\text{\hspace{0.17em}}<\frac{3}{2}$}.

Biểu diễn tập nghiệm trên trục số

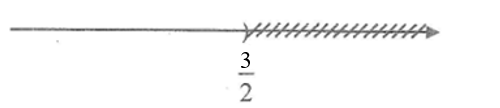
b) Ta có: 4x – 8 ≥ 3(3x – 2) + 4 – 2x

⇔ 4x – 8 ≥ 9x – 6 + 4 – 2x

⇔ 4x – 9x + 2x ≥ – 6 + 4 + 8

⇔ –3x ≥ 6

⇔ x ≤ –2

Vậy tập nghiệm của bất phương trình là

{x| x ≤ –2}

Bài 75 trang 61 SBT Toán 8 Tập 2: Giải các bất phương trình:

a) $2x+1,4\text{\hspace{0.17em}}<\frac{3x-7}{5}$;

b) $1+\frac{1+\text{\hspace{0.17em}\hspace{0.17em}}2x}{3}>\frac{2x-1}{6}-2$.

Lời giải:

a) $2x+1,4\text{\hspace{0.17em}}<\frac{3x-7}{5}$

$\iff (2x+1,4\text{\hspace{0.17em}}).5<\frac{3x-7}{5}.5$

 ⇔ 10x + 7 < 3x – 7

 ⇔ 10x – 3x < –7 – 7

 ⇔ 7x < –14

 ⇔ x < –2

Vậy tập nghiệm của bất phương trình là

S = {x| x < –2}

b) Ta có: $1+\frac{1+\text{\hspace{0.17em}\hspace{0.17em}}2x}{3}>\frac{2x-1}{6}-2$

$\iff 1.6+\frac{1+\text{\hspace{0.17em}\hspace{0.17em}}2x}{3}.6>\frac{2x-1}{6}.6-2.6$

⇔ 6 + 2 + 4x > 2x – 1 – 12

⇔ 4x – 2x > –1 – 12 – 6 – 2

⇔ 2x > –21

⇔ x > –10,5

Vậy tập nghiệm của bất phương trình là

S = {x| x > –10,5}.

Bài 76 trang 61 SBT Toán 8 Tập 2: Một người đi bộ quãng đường dài 18km trong khoảng thời gian không nhiều hơn 4 giờ. Lúc đầu người đó đi với vận tốc 5km/h, về sau đi với vận tốc 4km/h. Xác định độ dài đoạn đường mà người đó đã đi với vận tốc 5km/h.

Lời giải:

Gọi x (km) là đoạn đường người đó đi với vận tốc 5km/h. ĐK: x < 18.

Khi đó đoạn đường người đó đi với vận tốc 4km/h là 18 – x(km)

Thời gian đi với vận tốc 5km/h là $\frac{x}{5}$ giờ.

Thời gian đi với vận tốc 4km/h là $\frac{18-x}{4}$ giờ.

Vì thời gian đi hết đoạn đường không quá 4 giờ nên ta có bất phương trình:

$\frac{x}{5}\text{\hspace{0.17em}\hspace{0.17em}}+\frac{18-x}{4}\le 4$

$\iff \frac{x}{5}.20\text{\hspace{0.17em}}+\frac{18-x}{4}.20\le 4.20$

 ⇔ 4x + 90 – 5x ≤ 80

⇔ 4x – 5x ≤ 80 – 90

⇔ –x ≤ –10

⇔ x ≥ 10

Vậy đoạn đường đi với vận tốc 5km/h ít nhất là 10km.

Bài 77 trang 61 SBT Toán 8 Tập 2: Giải các phương trình:

a) |2x| = 3x – 2

b) |–3,5x| = 1,5x + 5

c) |x + 15| = 3x – 1

d) |2 – x| = 0,5x – 4

Lời giải:

a) Ta có: |2x| = 2x khi 2x ≥ 0 ⇔ x ≥ 0

Và |2x| = –2x khi 2x < 0 ⇔ x < 0

Ta có: 2x = 3x – 2

⇔ 2x – 3x = –2

⇔ x = 2

Giá trị x = 2 thỏa mãn điều kiện x ≥ 0 nên 2 là nghiệm của phương trình.

Xét –2x = 3x – 2

 ⇔ –2x – 3x = –2

 ⇔ $x=\frac{2}{5}$

Giá trị $x=\frac{2}{5}$ không thỏa mãn điều kiện x < 0 nên loại.

Vậy tập nghiệm của phương trình là S = {2}.

b) Ta có: |–3,5x| = –3,5x

khi –3,5x ≥ 0 ⇔ x ≤ 0

Và |–3,5x| = 3,5x

khi –3,5x < 0 ⇔ x > 0

Ta có: –3,5x = 1,5x + 5

 ⇔ –3,5x – 1,5x = 5

⇔ –5x = 5

 ⇔ x = –1

Giá trị x = –1 thỏa mãn

điều kiện x ≤ 0 nên –1 là nghiệm của phương trình.

Xét 3,5x = 1,5x + 5

 ⇔ 3,5x – 1,5x = 5

⇔ 2x = 5

 ⇔ x = 2,5

Giá trị x = 2,5 thỏa mãn điều kiện x > 0 nên 2,5 là nghiệm của phương trình.

Vậy tập nghiệm của phương trình là

S = {–1; 2,5}.

c) Ta có: |x + 15| = x + 15

khi x + 15 ≥ 0 ⇔ x ≥ –15

 Và |x + 15| = –x – 15

khi x + 15 < 0 ⇔ x < –15

Ta có: x + 15 = 3x – 1

 ⇔ x – 3x = –1 – 15

 ⇔ –2x = –16

 ⇔ x = 8

Giá trị x = 8 thỏa mãn

điều kiện x ≥ –15 nên 8 là nghiệm của phương trình.

Xét –x – 15 = 3x – 1

 ⇔ –x – 3x = –1 + 15

 ⇔ –4x = 14

 ⇔ x = –3,5

Giá trị x = –3,5 không thỏa mãn

điều kiện x < –15 nên loại.

Vậy tập nghiệm của phương trình là S = {8}.

d) Ta có: |2 – x| = 2 – x

khi 2 – x ≥ 0 ⇔ x ≤ 2

 Và  |2 – x| = x – 2

khi 2 – x < 0 ⇔ x > 2

Ta có: 2 – x = 0,5x – 4

 ⇔ –x – 0,5x = – 4 – 2

 ⇔ – 1,5x = – 6

 ⇔ x = 4

Giá trị x = 4 không thỏa mãn điều kiện x ≤ 2 nên loại.

Xét  x – 2 = 0,5x – 4

⇔ x – 0,5x = –4 + 2

 ⇔ 0,5x = –2

 ⇔ x = – 4

Giá trị x = – 4 không thỏa mãn

điều kiện x > 2 nên loại.

Vậy tập nghiệm của phương trình là S = ∅.

Bài 78 trang 61 SBT Toán 8 Tập 2: Chứng tỏ rằng, trong một tam giác độ dài một cạnh luôn nhỏ hơn nửa chu vi.

Lời giải:

Gọi a, b, c lần lượt là độ dài ba cạnh của tam giác.

Chu vi tam giác là a + b + c

Nửa chu vi tam giác là $\frac{a+b+\text{\hspace{0.17em}}c}{2}$

Theo bất đẳng thức tam giác, ta có:

a < b + c

⇔ a + a < a + b + c

 ⇔ 2a < a + b + c

⇔ $a\text{\hspace{0.17em}\hspace{0.17em}}<\frac{a+b+\text{\hspace{0.17em}}c}{2}$.

Tương tự: b < a + c

 ⇔ b + b < a + b + c

⇔ 2b < a + b + c

 ⇔  $b<\frac{a+b+\text{\hspace{0.17em}}c}{2}$.

Và c < a + b

⇔ c + c < a + b + c

⇔ 2c < a + b + c

⇔ $c<\frac{a+\text{\hspace{0.17em}\hspace{0.17em}}b+\text{\hspace{0.17em}}c}{2}$.

Vậy trong một tam giác độ dài một cạnh luôn nhỏ hơn nửa chu vi.

Bài 79 trang 61 SBT Toán 8 Tập 2: Với số m và số n bất kì, chứng tỏ rằng:

a) (m + 1)² ≥ 4m;

b) m² + n² + 2 ≥ 2(m + n).

Lời giải:

a) Ta có: (m – 1)² ≥ 0 với mọi m

⇔ (m – 1)² + 4m ≥ 4m

⇔ m² – 2m + 1 + 4m ≥ 4m

⇔ m² + 2m + 1 ≥ 4m

⇔ (m + 1)² ≥ 4m  (điều phải chứng minh).

b) Ta có: (m – 1)² ≥ 0; (n – 1)² ≥ 0 với mọi m, n

⇒ (m – 1)² + (n – 1)² ≥ 0

⇔ m² – 2m + 1 + n² – 2n + 1 ≥ 0

 ⇔ m² + n² + 2 ≥ 2(m + n)   (điều phải chứng minh).

Bài 80 trang 61 SBT Toán 8 Tập 2: Cho a > 0 và b > 0, chứng tỏ rằng: $(a+b).\left(\frac{1}{a}+\frac{1}{b}\text{}\right)\ge 4$.

Lời giải:

Ta có: (a – b)² ≥ 0 với mọi a, b

⇔ a² + b² – 2ab ≥ 0

⇔ a² + b² – 2ab + 2ab ≥ 2ab

⇔ a² + b² ≥ 2ab    (1)

Vì a > 0, b > 0 nên ab > 0 ⇒ $\frac{1}{ab}$ > 0  (2)

Từ (1); (2) suy ra:

(a² + b²).$\frac{1}{ab}$  ≥ 2ab.$\frac{1}{ab}$

⇔ $\frac{a}{b}+\frac{b}{a}$ ≥ 2

⇔ 2 + $\frac{a}{b}+\frac{b}{a}$ ≥  2 + 2

 ⇔ 2 + $\frac{a}{b}+\frac{b}{a}$ ≥ 4

⇔ 1 + 1 + $\frac{a}{b}+\frac{b}{a}$ ≥ 4

⇔ $\frac{a}{a}\text{\hspace{0.17em}\hspace{0.17em}}+\text{\hspace{0.17em}\hspace{0.17em}}\frac{b}{b}+\text{\hspace{0.17em}\hspace{0.17em}}\frac{a}{b}+\frac{b}{a}$  ≥ 4

⇔ $a\left(\frac{1}{a}\text{\hspace{0.17em}\hspace{0.17em}}+\text{\hspace{0.17em}}\frac{1}{b}\right)+\text{}b\left(\frac{1}{a}\text{\hspace{0.17em}\hspace{0.17em}}+\frac{1}{b}\right)$ ≥ 4

⇔ $(a+b).\left(\frac{1}{a}+\frac{1}{b}\text{}\right)\ge 4$ (điều phải chứng minh).

Bài 81 trang 62 SBT Toán 8 Tập 2: Chứng tỏ diện tích của hình vuông có cạnh 10m không nhỏ hơn diện tích hình chữ nhật có cùng chu vi.

Lời giải:

Chu vi hình vuông là 4.10 = 40 (m)

Suy ra, chu vi hình chữ nhật là 40 (m) nên nửa chu vi hình chữ nhật là 40 : 2 = 20 (m)

Gọi x (m) là chiều rộng hình chữ nhật.

Điều kiện: x < 20.

Khi đó chiều dài hình chữ nhật là 20 – x (m).

Diện tích hình chữ nhật là x(20 – x) (m²).

Vậy ta cần chứng minh: 10² ≥  x(20 – x)

Ta có: (10 – x)² ≥ 0 với mọi x

⇔ 10² – 20x + x² ≥ 0

⇔ 10² ≥ 20x – x²

 ⇔ 10² ≥ x(20 – x) (đcpcm)

Vậy diện tích hình vuông cạnh 10m không nhỏ hơn diện tích hình chữ nhật cùng chu vi.

Bài 82 trang 62 SBT Toán 8 Tập 2: Giải các bất phương trình:

a) 3(x – 2)(x + 2) < 3x² + x;

b) (x + 4)(5x – 1) > 5x² + 16x + 2.

Lời giải:

a) Ta có: 3(x – 2)(x + 2) < 3x² + x

⇔ 3(x² – 4) < 3x² + x

⇔ 3x² – 12 < 3x² + x

 ⇔ 3x² – 3x² – x < 12

 ⇔ –x < 12

⇔ x > –12

Vậy tập nghiệm của bất phương trình là

S = {x| x > –12}.

b) Ta có:

(x + 4)(5x – 1) > 5x² + 16x + 2

⇔ 5x² – x + 20x – 4 > 5x² + 16x + 2

⇔ 5x² – x + 20x – 5x² – 16x > 2 + 4

⇔ 3x > 6

⇔ x > 2

Vậy tập nghiệm của bất phương trình là

S = {x| x > 2}.

Bài 83 trang 62 SBT Toán 8 Tập 2: Giải các bất phương trình:

a) $\frac{5x^2-3x}{5}\text{\hspace{0.17em}\hspace{0.17em}}+\frac{3x+1}{4}<\frac{x(2x+1)}{2}-\frac{3}{2}$;

b) $\frac{5x-20}{3}-\frac{2x^2\text{}+\text{\hspace{0.17em}\hspace{0.17em}}x}{2}>\frac{x(1-3x)}{3}-\frac{5x}{4}$.

Lời giải:

a) Ta có:

$\frac{5x^2-3x}{5}\text{\hspace{0.17em}\hspace{0.17em}}+\frac{3x+1}{4}<\frac{x(2x+1)}{2}-\frac{3}{2}$

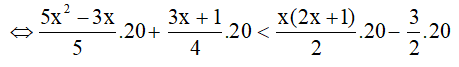
⇔ 20x² – 12x + 15x + 5 < 20x² + 10x – 30

⇔ 20x² – 12x + 15x – 20x² – 10x < –30 – 5

⇔ –7x < –35

⇔ x > 5

Vậy tập nghiệm của bất phương trình là

S = {x| x > 5}

b)Ta có:

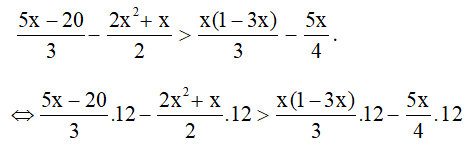
⇔ 20x – 80 – 12x² – 6x > 4x – 12x² – 15x

 ⇔ 20x – 12x² – 6x – 4x + 12x² + 15x > 80

⇔ 25x > 80

⇔ x > 3,2

Vậy tập nghiệm của bất phương trình là

S = {x| x > 3,2}.

Bài 84 trang 62 SBT Toán 8 Tập 2: Với giá trị nào của x thì:

a) Giá trị của biểu thức $\frac{2x-3}{35}+\frac{x(x-2)}{7}$ không lớn hơn giá trị của biểu thức $\frac{x^2}{7}-\frac{2x-3}{5}$.

b) Giá trị của biểu thức $\frac{6x\text{\hspace{0.17em}}+1}{18}+\frac{x+3}{12}$ không nhỏ hơn giá trị của biểu thức $\frac{5x+3}{6}+\text{\hspace{0.17em}}\frac{12-5x}{9}$.

Lời giải:

a) Giá trị của biểu thức $\frac{2x-3}{35}+\frac{x(x-2)}{7}$ không lớn hơn giá trị của biểu thức $\frac{x^2}{7}-\frac{2x-3}{5}$ nghĩa là $\frac{2x-3}{35}+\frac{x(x-2)}{7}\le \frac{x^2}{7}-\frac{2x-3}{5}$ .

Ta có: $\frac{2x-3}{35}+\frac{x(x-2)}{7}\le \frac{x^2}{7}-\frac{2x-3}{5}$

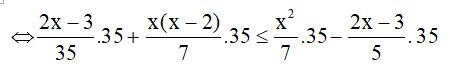
⇔ 2x – 3 + 5x² – 10x ≤ 5x² – 14x + 21

⇔ 2x + 5x² – 10x – 5x² + 14x ≤ 21 + 3

⇔ 6x ≤ 24

⇔ x ≤ 4

Vậy với x ≤ 4 thì giá trị của biểu thức $\frac{2x-3}{35}+\frac{x(x-2)}{7}$  không lớn hơn giá trị của biểu thức $\frac{x^2}{7}-\frac{2x-3}{5}$.

b) Giá trị của biểu thức $\frac{6x\text{\hspace{0.17em}}+1}{18}+\frac{x+3}{12}$ không nhỏ hơn giá trị của biểu thức $\frac{5x+3}{6}+\text{\hspace{0.17em}}\frac{12-5x}{9}$ nghĩa là $\frac{6x\text{\hspace{0.17em}}+1}{18}+\frac{x+3}{12}\ge \frac{5x+3}{6}+\text{\hspace{0.17em}}\frac{12-5x}{9}$

Ta có: 

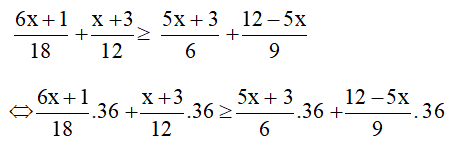
⇔ 12x + 2 + 3x + 9 ≥ 30x + 18 + 48 – 20x

⇔ 12x + 3x – 30x + 20x ≥ 18 + 48 – 2 – 9

⇔ 5x ≥ 55

⇔ x ≥ 11

Vậy với x ≥ 11 thì giá trị của biểu thức $\frac{6x\text{\hspace{0.17em}}+1}{18}+\frac{x+3}{12}$  không nhỏ hơn giá trị của biểu thức $\frac{5x+3}{6}+\text{\hspace{0.17em}}\frac{12-5x}{9}$.

Bài 85 trang 62 SBT Toán 8 Tập 2: Tìm x sao cho:

a) –x² < 0.

b) (x – 1)x < 0.

Lời giải:

a) Ta có: –x² < 0 ⇔ x² > 0

Mọi giá trị x ≠ 0 đều là nghiệm của bất phương trình.

Tập hợp các giá trị của x là

S = {x ∈ R| x ≠ 0}.

b) Trường hợp 1: x – 1 > 0 và x < 0

Ta có: x – 1 > 0 ⇔ x > 1 và x < 0

Điều này không xảy ra: loại.

Trường hợp 2: x – 1 < 0 và x > 0

Ta có: x – 1 < 0 ⇔ x < 1 và x > 0

Suy ra: 0 < x < 1

Vậy tập hợp các giá trị của x là

S = {x| 0 < x < 1}

Bài 86 trang 62 SBT Toán 8 Tập 2: Tìm x sao cho:

a) x² > 0.

b) (x – 2)(x – 5) > 0.

Lời giải:

a) Với x² > 0 thì mọi x khác 0 đều thỏa mãn bài toán.

Tập hợp các giá trị của x là

S = {x ∈ R| x ≠ 0}

b) Trường hợp 1: x – 2 > 0 và x – 5 > 0

Ta có: x – 2 > 0 ⇔ x > 2

x – 5 > 0 ⇔ x > 5

Suy ra: x > 5

Trường hợp 2: x – 2 < 0 và x – 5 < 0

Ta có: x – 2 < 0 ⇔ x < 2

x – 5 < 0 ⇔ x < 5

Suy ra: x < 2

Vậy với x > 5 hoặc x < 2

thì (x – 2)(x – 5) > 0.

Bài 87 trang 62 SBT Toán 8 Tập 2: Với giá trị nào của x thì:

a) $\frac{x-2}{x-3}>0$;

b) $\frac{x+\text{\hspace{0.17em}}2}{x-5}<0$.

Lời giải:

a) Trường hợp 1: x – 2 > 0 và x – 3 > 0

Ta có: x – 2 > 0 ⇔ x > 2

x – 3 > 0 ⇔ x > 3

Suy ra: x > 3

Trường hợp 2: x – 2 < 0 và x – 3 < 0

Ta có: x – 2 < 0 ⇔ x < 2

x – 3 < 0 ⇔ x < 3

Suy ra: x < 2

Vậy với x > 3 hoặc x < 2 thì $\frac{x-2}{x-3}>0$.

b) Trường hợp 1: x + 2 > 0 và x – 5 < 0

Ta có: x + 2 > 0 ⇔ x > –2

x – 5 < 0 ⇔ x < 5

Suy ra: –2 < x < 5

Trường hợp 2: x + 2 < 0 và x – 5 > 0

Ta có: x + 2 < 0 ⇔ x < –2

x – 5 > 0 ⇔ x > 5

Trường hợp trên không xảy ra.

Vậy với –2 < x < 5 thì $\frac{x+\text{\hspace{0.17em}}2}{x-5}<0$.

Bài 88 trang 62 SBT Toán 8 Tập 2: Chứng tỏ các phương trình sau vô nghiệm:

a) |2x + 3| = 2x + 2;

b) |5x – 3| = 5x – 5.

Lời giải:

a) Ta có: |2x + 3| = 2x + 3

khi 2x + 3 ≥ 0 ⇔ x ≥ –1,5

Và |2x + 3| = –2x – 3

khi 2x + 3 < 0 ⇔ x < –1,5

Ta có: 2x + 3 = 2x + 2 ⇔ 0x = –1 phương trình vô nghiệm.

Xét  –2x – 3 = 2x + 2

 ⇔ –2x – 2x = 2 + 3

 ⇔ –4x = 5

 ⇔ x = –1,25

Giá trị x = –1,25 không thỏa mãn điều kiện x < –1,5 nên loại.

Vậy phương trình đã cho vô nghiệm.

b) Ta có: |5x – 3| = 5x – 3

khi 5x – 3 ≥ 0 ⇔ x ≥ 0,6

Và |5x – 3| = 3 – 5x

khi 5x – 3 < 0 ⇔ x < 0,6

Ta có: 5x – 3 = 5x – 5 ⇔ 0x = –2 phương trình vô nghiệm.

Xét: 3 – 5x = 5x – 5

⇔ –5x – 5x = –5 – 3

⇔ –10x = –8

⇔ x = 0,8

Giá trị x = 0,8 không thỏa mãn

điều kiện x < 0,6 nên loại.

Vậy phương trình đã cho vô nghiệm.

Bài tập bổ sung

Bài IV.1 trang 62 SBT Toán 8 Tập 2: Tìm x sao cho $\frac{2x-1}{x+3}>1$

Xem thêm lời giải sách bài tập Toán học lớp 8 hay, chi tiết khác:

Bài 1: Liên hệ giữa thứ tự và phép cộng

Bài 2: Liên hệ giữa thứ tự và phép nhân

Bài 3: Bất phương trình một ẩn

Bài 4: Bất phương trình bậc nhất một ẩn

Bài 5: Phương trình chứa dấu giá trị tuyệt đối

Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

Lý thuyết Ôn tập chương 4

Trắc nghiệm Bài ôn tập chương 4 có đáp án