SBT Toán 8 Bài 12: Hình vuông

Mục lục Giải SBT Toán 8 Bài 12: Hình vuông

Bài 144 trang 98 SBT Toán 8 Tập 1: Cho tam giác ABC vuông tại A, đường phân giác AD. Gọi M, N là chân đường vuông góc kẻ từ D đến AB, AC. Chứng minh rằng tứ giác AMDN là hình vuông.

Lời giải:

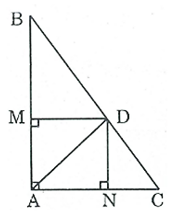
Xét tứ giác AMDN, ta có:

$\widehat{MAN}$ = 90° (giả thiết)

DM ⊥ AB (giả thiết)

⇒$\widehat{AMD}$ = 90°

DN ⊥ AC (giả thiết)

⇒$\widehat{AND}$ = 90°

Suy ra tứ giác AMDN là hình chữ nhật.

(vì có ba góc vuông)

Lại có hình chữ nhật AMDN có đường chéo AD là đường phân giác của A.

Vậy hình chữ nhật AMDN là hình vuông.

Bài 145 trang 98 SBT Toán 8 Tập 1: Cho hình vuông ABCD. Trên AB, BC, CD, DA lấy theo thứ tự các điểm E, K, P, Q sao cho AE = BK = CP = DQ. Tứ giác EKPQ là hình gì? Vì sao?

Lời giải:

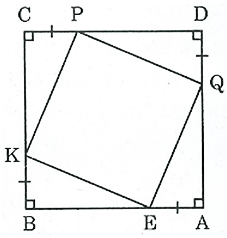
Ta có: AB = BC = CD = DA

Và AE = BK = CP = DQ

Suy ra: EB = KC = PD = QA

* Xét ΔAEQ và ΔBKE, ta có:

AE = BK

$\widehat{EAQ}=\widehat{KBE}$ = 90^o

QA = EB (chứng minh trên)

Do đó, ΔAEQ = ΔBKE (c.g.c)

⇒ EQ = EK (1)

* Xét ΔBKE và ΔCPK, ta có:

BK = CP

$\widehat{KBE}=\widehat{PCK}$ = 90^o

EB = KC (chứng minh trên)

Suy ra: ΔBKE = ΔCPK (c.g.c)

⇒ EK = KP (2)

* Xét ΔCPK và ΔDQP,ta có:

CP = DQ

$\widehat{C}=\widehat{D}$ = 90^o

DP = CK (chứng minh trên)

Suy ra: ΔCPK = ΔDQP (c.g.c)

⇒ KP = PQ (3)

Từ (1), (2) và (3) suy ra:

EK = KP = PQ = EQ.

Hay tứ giác EKPQ là hình thoi.

Mặt khác: ΔAEQ = ΔBKE.

⇒ $\widehat{AQE}=\widehat{BEK}$

Mà $\widehat{AQE}+\widehat{AEQ}$ = 90^o

⇒ $\widehat{BEK}+\widehat{AEQ}$ = 90^o

Ta có:

 $\widehat{BEK}+\text{\hspace{0.17em}\hspace{0.17em}}\widehat{QEK}+\text{\hspace{0.17em}\hspace{0.17em}}\widehat{AEQ}={180}^0$

Suy ra:

$\begin{array}{l}\widehat{QEK}={180}^0-\left(\widehat{BEK}+\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}\widehat{AEQ}\right)\\ ={180}^0-{90}^0={90}^0\end{array}$

Vậy tứ giác EKPQ là hình vuông.

Bài 146 trang 98 SBT Toán 8 Tập 1: Cho tam giác ABC, điểm I nằm giữa B và C. Qua I vẽ đường thẳng song song với AB, cắt AC ở H. Qua I vẽ đường thẳng song song với AC, cắt AB ở K.

a) Tứ giác AHIK là hình gì?

b) Điểm I ở vị trí nào trên BC thì tứ giác AHIK là hình thoi

c) Tam giác ABC có điều kiện gì thì tứ giác AHIK là hình chữ nhật.

Lời giải:

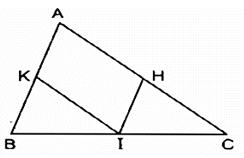
a) Xét tứ giác AHIK có:

IK // AC hay IK // AH

Lại có: IH // AB  hay IH // AK

Vậy tứ giác AHIK là hình bình hành.

b)

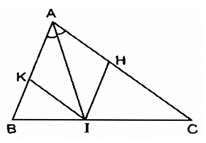
 Hình bình hành AHIK là hình thoi nên đường chéo AI là phân giác của $\widehat{BAC}$

Ngược lại nếu AI là phân giác của $\widehat{BAC}$ thì hình bình hành AHIK có đường chéo AI là phân giác của một góc nên hình bình hành AHIK là hình thoi.

Vậy nếu I là giao điểm của đường phân giác của $\widehat{A}$ với cạnh BC thì tứ giác AHIK là hình thoi.

c) Hình bình hành AHIK là hình chữ nhật

⇒$\widehat{A}$ = 90^o suy ra ΔABC vuông tại A.

Ngược lại ΔABC có $\hat{A}$ = 90^o

Suy ra hình bình hành AHIK là hình chữ nhật.

Vậy nếu ΔABC vuông tại A thì tứ giác AHIK là hình chữ nhật.

Bài 147 trang 98 SBT Toán 8 Tập 1: Hình chữ nhật ABCD có AB = 2AD. Gọi P, Q theo thứ tự là trung điểm của AB, CD. Gọi H là giao điểm của AQ và DP, gọi K là giao điểm của CP và BQ. Chứng minh rằng PHQK là hình vuông.

Lời giải:

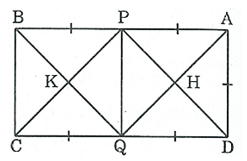
* Xét tứ giác APQD, ta có:

AB // CD hay AP // QD

AP = $\frac{1}{2}$.AB

QD = $\frac{1}{2}$CD

AB = CD (vì ABCD là hình chữ nhật)

Suy ra: AP = QD

Xét tứ giác APQD có:

AP = QD

AP // QD

Do đó, tứ giác APQD là hình bình hành.

Lại có: $\hat{A}$ = 90^o (vì tứ giác ABCD là hình chữ nhật)

Suy ra tứ giác APQD là hình chữ nhật.

Mà AD = AP = $\frac{1}{2}$AB.

Vậy tứ giác APQD là hình vuông.

⇒ AQ ⊥ PD (tính chất hình vuông)

⇒ $\widehat{PHQ}$ = 90^o 

HP = HQ (tính chất hình vuông)

* Xét tứ giác PBCQ, ta có:

AB // CD hay BP //CQ

PB = $\frac{1}{2}$AB

CQ = $\frac{1}{2}$CD

AB = CD do ABCD là hình chữ nhật.

Suy ra: PB = CQ nên tứ giác PBCQ là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).

Lại có: $\hat{B}$ = 90^o (vì ABCD là hình chữ nhật)

Suy ra tứ giác PBCQ là hình chữ nhật.

Lại có: PB = BC (vì cùng bằng AD = $\frac{1}{2}$AB)

Vậy tứ giác PBCQ là hình vuông

⇒ PC ⊥ BQ (tính chất hình vuông)

⇒ $\widehat{PKQ}$ = 90^o 

PD là tia phân giác $\widehat{APQ}$ (tính chất hình vuông)

PC là tia phân giác $\widehat{QPB}$ (tính chất hình vuông)

Suy ra: PD ⊥ PC (tính chất tia phân giác của hai góc kề bù)

⇒$\widehat{HPK}$ = 90^o 

Xét tứ giác PHQK có:

$\widehat{PHQ}$ = 90^o (chứng minh trên)

$\widehat{HPK}$ = 90^o (chứng minh trên)

$\widehat{PKQ}$ = 90^o (chứng minh trên)

Do đó, tứ giác PHQK là hình chữ nhật

Mặt khác, PH = HQ (chứng minh trên)

Suy ra tứ giác PHQK là hình vuông.

Bài 148 trang 98 SBT Toán 8 Tập 1: Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy các điểm H, G sao cho BH = HG = GC. Qua H và G kẻ các đường vuông góc với BC chúng cắt AB, AC theo thứ tự ở E và F. Tứ giác EFGH là hình gì? Vì sao?

Lời giải:

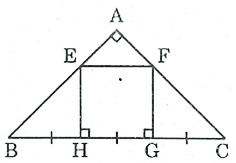
Vì ΔABC vuông cân tại A nên $\widehat{B}=\widehat{C}$ = 45^o

Vì ΔBHE vuông tại H có $\widehat{B}$ = 45^o nên ΔBHE vuông cân tại H.

Suy ra HB = HE

Vì ΔCGF vuông tại G, có $\widehat{C}$ = 45^o nên ΔCGF vuông cân tại G

Suy ra GC = GF.

Ta có: BH = HG = GC (giả thiết)

Suy ra: HE = HG = GF.

Vì EH // GF (hai đường thẳng cùng vuông góc với đường thắng thứ ba)

Xét tứ giác HEFG có:

EH // GF

HE = GF

Do đó, tứ giác HEFG là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).

Lại có $\widehat{EHG}$ = 90^o nên HEFG là hình chữ nhật.

Mà EH = HG (chứng minh trên).

Do đó, HEFG là hình vuông (hình chữ nhật có hai cạnh kề bằng nhau là hình vuông)

Bài 149 trang 98 SBT Toán 8 Tập 1: Cho hình vuông ABCD. Trên cạnh AD lấy điểm F, trên cạnh DC lấy điểm E sao cho AF = DE. Chứng minh rằng AE = BF và AE ⊥ BF.

Lời giải:

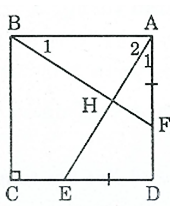
Xét ΔABF và ΔDAE,ta có:

AB = DA (giả thiết)

$\widehat{BAF}=\widehat{ADE}$ = 90^o

AF = DE (giả thiết)

Suy ra: ΔABF = ΔDAE (c.g.c)

⇒ BF = AE và $\widehat{B_1}=\widehat{A_1}$

Gọi H là giao điểm của AE và BF.

Ta có: $\widehat{BAF}=\widehat{A_1}\text{}+\widehat{A_2}$ = 90^o

Mà $\widehat{B_1}=\widehat{A_1}$

Suy ra: $\widehat{B_1}+\widehat{A_2}$ = 90^o

Trong ΔABH, ta có:

 $\widehat{AHB}=\widehat{B_1}+\widehat{A_2}$ = 180^o

⇒ $\widehat{AHB}$ = 180^o – ($\widehat{B_1}+\widehat{A_2}$ )

= 180^o – 90^o = 90^o

Vậy AE ⊥ BF.

Bài 150 trang 98 SBT Toán 8 Tập 1: Cho hình chữ nhật có hai cạnh kề không bằng nhau. Chứng minh rằng các tia phân giác của các góc của hình chữ nhật đó cắt nhau tạo thành một hình vuông.

Lời giải:

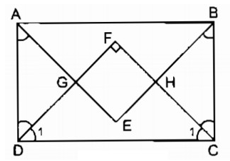
Gọi giao điểm các đường phân giác của các góc: A, B, C, D theo thứ tự cắt nhau tại E, H, F, G.

* Trong ΔADG , ta có:

$\widehat{GAD}$ = 45^o; $\widehat{GDA}$ = 45^o (vì DG; AG là tia phân giác của góc $\widehat{ADC};\widehat{BAD}$)

Suy ra:

$$\begin{gathered} \widehat{AGD}={180}^0-\widehat{GAD}-\widehat{GDA} \\ ={90}^0 \end{gathered}$$

⇒ ΔGAD vuông cân tại G.

⇒ GD = GA

Trong ΔBHC, ta có:

$\widehat{HBC}$ = 45^o; $\widehat{HCB}$ = 45^o (gt)

Suy ra:  

$\begin{array}{l}\widehat{BHC}={180}^0-\widehat{HBC}-\widehat{HCB}\\ ={90}^0\end{array}$

⇒ ΔHBC vuông cân tại H.

⇒ HB = HC

* Trong ΔFDC, ta có:

 $\widehat{D_1^{}}$ = 45^o; $\widehat{C_1}$ = 45^o 

Suy ra:

 $\widehat{F}$ = 180° - $\widehat{D_1}-\widehat{C_1}$

 = 90°

⇒ ΔFDC vuông cân tại F

⇒ FD = FC

Nên tứ giác EFGH là hình chữ nhật (vì có 3 góc vuông).

Xét ΔGAD và ΔHBC,ta có:

$\widehat{GAD}=\widehat{HBC}$ = 45^o

AD = BC (tính chất hình chữ nhật)

$\widehat{GDA}=\widehat{HCB}$ = 45^o

Suy ra: ΔGAD = ΔHBC ( g.c.g)

Do đó, GD = HC .

Lại có: FD = FC (chứng minh trên)

Suy ra: FG = FH.

Vậy hình chữ nhật EFGH có hai cạnh kề bằng nhau nên nó là hình vuông.

Bài 151 trang 98 SBT Toán 8 Tập 1: Cho hình vuông ABCD. Gọi E là một điểm nằm giữa C và D. Tia phân giác của góc DAE cắt CD ở F. Kẻ FH ⊥ AE (H ∈ AE), FH cắt BC ở G. Tính số đo .

Lời giải:

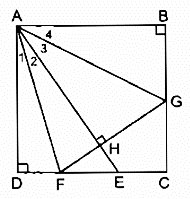
* Xét hai tam giác vuông DAF và HAF, ta có:

$\widehat{ADF}=\widehat{AHF}$ = 90^o

$\widehat{A_1}=\widehat{A_2}$(vì AF là tia phân giác của góc DAH)

AF cạnh huyền chung

Suy ra: ΔDAF = ΔHAF (cạnh huyền - góc nhọn)

⇒ DA = HA

Mà DA = AB (vì ABCD là hình vuông)

Suy ra: HA = AB.

* Xét hai tam giác vuông HAG và BAG, ta có:

$\widehat{AHG}=\widehat{ABG}$ = 90^o

HA = AB (chứng minh trên)

AG cạnh huyền chung

Suy ra: ΔHAG = ΔBAG (cạnh huyền - cạnh góc vuông)

⇒ $\widehat{A_3}=\widehat{A_4}$ hay AG là tia phân giác của $\widehat{EAB}$

Vậy 

$\begin{array}{l}\widehat{F\text{}A\text{}G}=\widehat{A_2\text{}}+\text{\hspace{0.17em}}\widehat{A_3}\\ =\frac{1}{2}\left(\widehat{DA\text{}E}+\text{\hspace{0.17em}}\widehat{EAB}\right)\\ =\frac{1}{2}.{90}^0={45}^0\end{array}$

Bài 152 trang 99 SBT Toán 8 Tập 1: Cho hình vuông DEBC. Trên cạnh DC lấy điểm A, trên tia đối của tia DC lấy điểm K, trên tia đối của tia ED lấy điểm M sao cho CA = DK = EM . Vẽ hình vuông DKIH (H thuộc cạnh DE). Chứng minh rằng ABMI là hình vuông.

Lời giải:

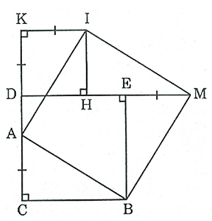
* Xét ΔCAB và ΔEMB, ta có:

CA = EM

$\widehat{ACB}=\widehat{MEB}$ = 90°

CB = EB (tính chất hình vuông)

Suy ra: ΔCAB = ΔEMB (c.g.c)

⇒ AB = MB (1)

Ta có: AK = DK+ DA

Và CD = CA + AD

Mà CA = DK nên AK = CD

* Xét ΔCAB và ΔKIA, ta có:

CA = KI (vì cùng bằng DK)

$\widehat{C}=\widehat{AKI}$ = 90^o

CB = AK (vì cùng bằng CD)

Suy ra: ΔCAB = ΔKIA (c.g.c)

⇒ AB = AI (2)

Ta có: DH = DK (vì KDHI là hình vuông)

Và EM = DK (giả thiết)

Suy ra: DH = EM

⇒ DH + HE = HE + EM

Hay DE = HM.

* Xét ΔHIM và ΔEMB, ta có:

HI = EM (vì cùng bằng DK)

$\widehat{IHM}=\widehat{MEB}$ = 90^o

HM = EB (vì cùng bằng DE)

Suy ra: ΔHIM = ΔEMB (c.g.c)

⇒ IM = MB (3)

Từ (1), (2) và (3) suy ra:

AB = BM = AI = IM.

Tứ giác ABMI là hình thoi.

Mặt khác, ta có ΔACB = ΔMEB (chứng minh trên)

⇒ $\widehat{CBA}=\widehat{EBM}$

Mà $\widehat{CBA}+\widehat{A\text{}BE}\text{\hspace{0.17em}\hspace{0.17em}}=\widehat{CBE}={90}^0$

Suy ra: $\widehat{EBM}+\text{\hspace{0.17em}}\widehat{ABE}$ = 90^o hay $\widehat{ABM}$ = 90^o

Vậy tứ giác ABMI là hình vuông.

Bài 153 trang 99 SBT Toán 8 Tập 1: Cho tam giác ABC. Vẽ ở ngoài tam giác các hình vuông ABDE, ACFH.

a) Chứng minh rằng EC = BH, EC ⊥ BH

b) Gọi M, N theo thứ tự là tâm của các hình vuông ABDE, ACFH. Gọi I là trung điểm của BC. Tam giác MIN là tam giác gì? Vì sao?

Lời giải:

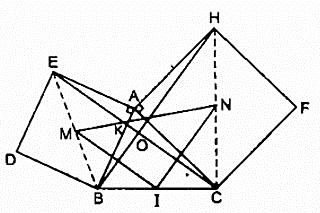
a) Ta có:

$\begin{array}{l}\widehat{BAH}=\widehat{BAC}\text{\hspace{0.17em}\hspace{0.17em}}+\text{\hspace{0.17em}\hspace{0.17em}}\widehat{CAH}\\ \\ =\widehat{BAC}+\text{\hspace{0.17em}\hspace{0.17em}}{90}^0\end{array}$

$\begin{array}{l}\widehat{EAC}=\widehat{BAC}+\text{\hspace{0.17em}\hspace{0.17em}}\widehat{BAE}\\ =\widehat{BAC}+\text{\hspace{0.17em}\hspace{0.17em}}{90}^0\end{array}$

Suy ra: $\widehat{BAH}=\widehat{EAC}$

* Xét ΔBAH và ΔEAC , ta có:

BA = EA (vì ABDE là hình vuông)

$\widehat{BAH}=\widehat{EAC}$ (chứng minh trên)

AH = AC (vì ACFH là hình vuông)

Suy ra: ΔBAH = ΔEAC (c.g.c)

⇒ BH = EC

Gọi K và O lần lượt là giao điểm của EC với AB và BH.

Ta có: $\widehat{AEC}=\widehat{ABH}$ (vì ΔBAH = ΔEAC) (1)

Hay $\widehat{AEK}=\widehat{OBK}$

* Trong ΔAEK, ta có:

$\widehat{EAK}$ = 90^o

⇒ $\widehat{AEK}+\text{\hspace{0.17em}\hspace{0.17em}}\widehat{AKE}$ = 90^o (2)

Mà $\widehat{AKE}=\widehat{OKB}$ (đối đỉnh) (3)

Từ (1), (2) và (3) suy ra:

$\widehat{OKB}+\text{\hspace{0.17em}}\widehat{OBK}$ = 90^o

* Trong Δ BOK ta có:

$\widehat{BOK}+\widehat{OKB}+\text{\hspace{0.17em}\hspace{0.17em}}\widehat{OBK}={180}^0$

$\begin{array}{l}\widehat{BOK}={180}^0-\left(\widehat{OKB}+\text{\hspace{0.17em}\hspace{0.17em}}\widehat{OBK}\right)\\ ={180}^0-{90}^0={90}^0\end{array}$

Suy ra: EC ⊥ BH

b) * Trong ΔEBC , ta có:

M là trung điểm EB (tính chất hình vuông)

Và I trung điểm BC

Nên MI là đường trung bình của ΔEBC

⇒ MI = $\frac{1}{2}$EC và MI // EC (tính chất đường trung bình của tam giác).

Trong ΔBCH, ta có:

I trung điểm BC

Và N trung điểm của CH (tính chất hình vuông)

Nên NI là đường trung bình của ΔBCH

⇒ NI = $\frac{1}{2}$BH và NI // BH (tính chất đường trung bình của tam giác)

Mà BH = CE (chứng minh trên)

Suy ra: MI = NI nên ΔINM cân tại I.

Ta có: MI // EC (chứng minh trên)

 Và EC ⊥ BH (chứng minh trên)

Suy ra: MI ⊥ BH. Mà NI // BH (chứng minh trên)

Suy ra: MI ⊥ NI hay $\widehat{MIN}$ = 90^o

Vậy ΔMIN vuông cân tại I.

Bài 154 trang 99 SBT Toán 8 Tập 1: Cho hình vuông ABCD, điểm E thuộc cạnh CD. Tia phân giác của góc ABE cắt AD ở K. Chứng minh rằng AK + CE = BE.

Lời giải:

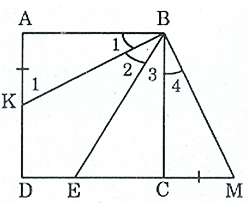
Trên tia đối của tia CD lấy điểm M sao cho CM = AK

Ta có: AK + CE = CM + CE = EM (1)

Xét ΔABK và ΔCBM, ta có:

AB = CB (vì ABCD là hình vuông)

$\widehat{A}=\widehat{BCM}$ = 90^o

AK = CM (theo cách vẽ)

Suy ra: ΔABK = ΔCBM (c.g.c)

⇒ $\widehat{B_1}=\widehat{B_4}$ (2)

Lại có: $\widehat{B_1}=\widehat{B_2}$ (do BK là tia phân giác của ABE)

Suy ra: $\widehat{B_1}=\widehat{B_2}=\widehat{B_4}$

Mà $\widehat{KBC}$ = 90^o - $\widehat{B_1}$ (3)

Tam giác CBM vuông tại C nên:

 $\widehat{M}$ = 90^o - $\widehat{B_4}$ (4)

Từ (2), (3) và (4) suy ra:

$\widehat{KBC}=\widehat{M}$ (5)

Hay $\widehat{B_2}+\widehat{B_3}=\widehat{M}$

⇒ $\widehat{B_4}+\widehat{B_3}=\widehat{M}$ (vì $\widehat{B_4}=\widehat{B_2}$)

Hay: $\widehat{EBM}=\widehat{M}$

⇒ ΔEBM cân tại E

⇒ EM = BE. (6)

Từ (1) và (6) suy ra:

AK + CE = BE.

Bài 155 trang 99 SBT Toán 8 Tập 1: Cho hình vuông ABCD. Gọi E, F theo thứ tự là trung điểm của AB, BC.

a) Chứng minh rằng CE vuông góc với DF.

b) Gọi M là giao điểm của CE và DF. Chứng minh rằng AM = AD.

Hướng dẫn: Gọi K là trung điểm của CD. Chứng minh rằng KA // CE.

Lời giải:

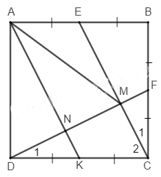
a) Xét ΔBEC và ΔCFD, ta có:

BE = CF (giả thiết)

$\widehat{B}=\widehat{C}$ = 90^o

BC = CD (vì ABCD là hình vuông)

Suy ra: ΔBEC = ΔCFD (c.g.c)

⇒ $\widehat{C_1}=\widehat{D_1}$

Lại có: $\widehat{C_1}+\widehat{C_2}$ = 90^o

Suy ra: $\widehat{D_1}+\widehat{C_2}$ = 90^o

Trong ΔDCM có $\widehat{D_1}+\widehat{C_2}$ = 90^o

Suy ra: $\widehat{DMC}$ = 90^o

Vậy CE ⊥ DF.

b) Gọi K là trung điểm của DC, AK cắt DF tại N.

* Xét tứ giác AKCE, ta có: AB // CD hay AE // CK

AE = $\frac{1}{2}$AB

CK = $\frac{1}{2}$CD (theo cách vẽ)

AB = CD ( Vì ABCD là hình vuông)

Suy ra: AE = CK nên tứ giác AKCE là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)

⇒ AK // CE

DF ⊥ CE (chứng minh trên)

⇒ AK ⊥ DF hay AN ⊥ DM (quan hệ từ vuông góc đến song song)

* Trong ΔDMC, ta có:

DK = KC và KN // CM

Nên DN = MN (tính chất đường trung bình của tam giác)

Tam giác ADM có AN là đường cao đồng thời là đường trung tuyến

Suy ra: ΔADM cân tại A.

Vậy AD = AM.

Bài 156 trang 99 SBT Toán 8 Tập 1: Cho hình vuông ABCD. Vẽ điểm E trong hình vuông sao cho $\widehat{EDC}=\widehat{ECD}$ = 15^o

a) Vẽ điểm F trong hình vuông sao cho $\widehat{FAD}=\widehat{FDA}$ = 15^o. Chứng minh rằng tam giác DEF là tam giác đều.

b) Chứng minh rằng tam giác ABE là tam giác đều.

Lời giải:

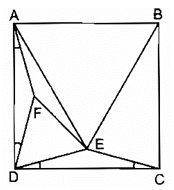
a) Xét ΔEDC và ΔFDA, ta có:

$\widehat{EDC}=\widehat{FDA}$ = 15^o

DC = AD (vì ABCD là hình vuông)

$\widehat{EDC}=\widehat{FAD}$ = 15^o

Suy ra: ΔEDC = ΔFDA (g.c.g)

⇒ DE = DF

⇒ ΔDEF cân tại D

Lại có:

$\widehat{ADC}=\widehat{FDA}+\text{\hspace{0.17em}}\widehat{F\text{}D\text{}E}+\text{\hspace{0.17em}\hspace{0.17em}}\widehat{E\text{}D\text{}C\text{}}$

$\begin{array}{l}\widehat{F\text{}D\text{}E}=\widehat{ADC}-\left(\widehat{FDA}+\text{\hspace{0.17em}\hspace{0.17em}}\widehat{E\text{}D\text{}C\text{}}\right)\\ ={90}^0-({15}^0+\text{}{15}^0)={60}^0\end{array}$

Vậy ΔDEF đều.

b) Xét ΔADE và ΔBCE , ta có:

ED = EC (vì AEDC cân tại E)

$\widehat{ADE}=\widehat{BCE}$ = 75^o

AD = BC (vì ABCD là hình vuông)

Suy ra: ΔADE = ΔBCE (c.g.c)

⇒ AE = BE (1)

* Trong ΔADE, ta có:

$\begin{array}{l}\widehat{A\text{}F\text{}D}={180}^0-\left(\widehat{F\text{}A\text{}D}\text{\hspace{0.17em}\hspace{0.17em}}+\widehat{F\text{}DA}\right)\\ ={180}^0-({15}^0+\text{}{15}^0)={150}^0\end{array}$

$\widehat{AF\text{}D}\text{\hspace{0.17em}\hspace{0.17em}}+\text{\hspace{0.17em}\hspace{0.17em}}\widehat{DF\text{}E}+\text{\hspace{0.17em}}\widehat{AF\text{}E}={360}^0$

$\begin{array}{l}\Rightarrow \widehat{AF\text{}E}={360}^0-\left(\widehat{AF\text{}D}+\widehat{DF\text{}E}\right)\\ ={360}^0-\left({150}^0+\text{}{60}^0\right)={150}^0\end{array}$

* Xét ΔAFD và ΔAFE, ta có: AF cạnh chung

$\widehat{AFD}=\widehat{AFE}$ = 150^o

DE = EF (vì ΔDFE đều)

Suy ra: ΔAFD = ΔAFE (c.g.c)

⇒ AE = AD

Mà AD = AB (vì ABCD hình vuông)

Suy ra: AE = AB (2)

Từ (1) và (2) suy ra:

AE = AB = BE.

Vậy ΔAEB đều.

Bài tập bổ sung

Bài 12.1 trang 99 SBT Toán 8 Tập 1: Hình vuông có chu vi bằng 8 thì đường chéo bằng...

Bài 12.2 trang 99 SBT Toán 8 Tập 1: Cho hình thoi ABCD, O là giao điểm của hai đường chéo. Các tia phân giác của bốn góc vuông có đỉnh O...

Bài 12.3 trang 99 SBT Toán 8 Tập 1: Cho hình vuông ABCD. Trên cạnh DC lấy điểm E, trên cạnh BC lấy điểm F sao cho DE = CF...

Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:

Ôn tập chương 1 - Phần Hình học

Bài 1: Đa giác - Đa giác đều

Bài 2: Diện tích hình chữ nhật

Bài 3: Diện tích tam giác

Bài 4: Diện tích hình thang

Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

Trắc nghiệm Hình vuông có đáp án