SBT Toán 8 Bài 4: Đường trung bình của tam giác, của hình thang

Mục lục Giải SBT Toán 8 Bài 4: Đường trung bình của tam giác, của hình thang

Bài 34 trang 84 SBT Toán 8 Tập 1: Cho tam giác ABC, điểm D thuộc cạnh AC sao cho AD = $\frac{1}{2}$DC. Gọi M là trung điểm của BC, I là giao điểm của BD và AM. Chứng minh: AI = IM.

Lời giải:

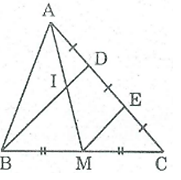
Gọi E là trung điểm của DC

Trong ΔBDC, ta có:

M là trung điểm của BC (gt)

E là trung điểm của CD (gt)

Nên ME là đường trung bình của ∆BCD

⇒ME // BD (tính chất đường trung bình tam giác)

Suy ra: DI // ME

Ta có: AD = $\frac{1}{2}$DC (gt)

DE = $\frac{1}{2}$DC (cách vẽ)

⇒ AD = DE nên D là trung điểm của AE

Xét tam giác AEM có:

 D là trung điểm của AE và DI // ME nên DI đi qua trung điểm của AM nên I là trung điểm của AM

Nên AI= IM (tính chất).

Bài 35 trang 84 SBT Toán 8 Tập 1: Hình thang ABCD có đáy AB, CD. Gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC. Chứng minh rằng ba điểm E, F, I thẳng hàng.

Lời giải:

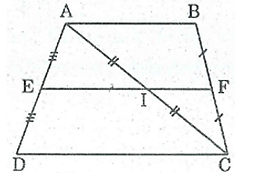
* Hình thang ABCD có AB // CD

E là trung điểm của AD và F là trung điểm của BC (gt)

Nên EF là đường trung bình của hình thang ABCD

EF // CD (tính chất đường trung bình hình thang) (1)

* Trong ΔADC ta có:

E là trung điểm của AD  và I là trung điểm của AC (gt)

Nên EI là đường trung bình của ΔADC

⇒ EI // CD (tính chất đường trung bình tam giác) (2)

Từ (1) và (2) và theo tiên đề Ơ-clít ta có đường thẳng EF và EI trùng nhau.

Vậy E, F, I thẳng hàng.

Bài 36 trang 84 SBT Toán 8 Tập 1: Cho tứ giác ABCD. Gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC. Chứng minh rằng:

a) EI // CD, IF // AB;

b) $E\text{}F\le \frac{AB+\text{\hspace{0.17em}\hspace{0.17em}}CD}{2}$.

Lời giải:

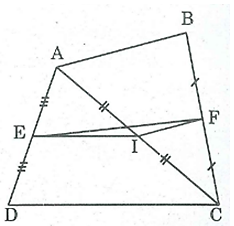
a) * Trong tam giác ADC, ta có:

E là trung điểm của AD và I là trung điểm của AC (gt)

Nên EI là đường trung bình của ΔADC.

⇒ EI // CD (tính chất đường trung bình của tam giác) và $\text{}E\text{}I=\frac{CD}{2}$

* Trong tam giác ABC, ta có:

I là trung điểm của AC và F là trung điểm của BC

Nên IF là đường trung bình của ΔABC.

⇒ IF // AB (tính chất đường trung bình của tam giác) và $I\text{}F=\frac{AB}{2}$

b) Với 3 điểm E, I, F bất kì ta có: EF ≤ EI + IF (dấu “ = ” xảy ra khi I nằm giữa E và F) mà $\text{}E\text{}I=\frac{CD}{2}$; $I\text{}F=\frac{AB}{2}$ (chứng minh trên)

⇒ $\text{EF\hspace{0.17em}}\le \frac{CD}{2}+\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}\frac{AB}{2}$

Vậy $E\text{}F\le \frac{AB+\text{\hspace{0.17em}\hspace{0.17em}}CD}{2}$(dấu bằng xảy ra khi AB // CD).

Bài 37 trang 84 SBT Toán 8 Tập 1: Cho hình thang ABCD (AB // CD), M là trung điểm của AD, N là trung điểm của BC. Gọi I, K theo thứ tự là giao điểm của MN với BD, AC. Cho biết AB = 6cm, CD = l4cm. Tính độ dài MI, IK, KN.

Lời giải:

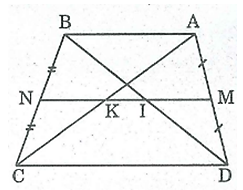
Hình thang ABCD có AB // CD

M là trung điểm của AD và N là trung điểm của BC (giả thiết)

Nên MN là đường trung bình của hình thang ABCD

⇒ MN // AB // CD

$\begin{array}{l}MN=\frac{AB+\text{\hspace{0.17em}}CD}{2}\\ =\frac{6+\text{\hspace{0.17em}}14}{2}=10cm\end{array}$

* Trong tam giác ADC, ta có:

M là trung điểm của AD

MK // CD

Do đó MK đi qua trung điểm của AC nên K là trung điểm AC

⇒ AK = KC và MK là đường trung bình của ΔADC.

⇒ MK = $\frac{1}{2}$CD

= $\frac{1}{2}$.14= 7 (cm)

Vậy: KN = MN – MK

= 10 – 7 = 3 (cm)

* Trong ΔADB, ta có:

M là trung điểm của AD

MI // AB

Do đó, MI đi qua trung điểm của BI nên I là trung điểm của BD  DI = IB

⇒ MI là đường trung bình của ΔDAB

⇒ MI = $\frac{1}{2}$AB

= $\frac{1}{2}$.6 = 3 (cm)

Và IK = MK – Ml = 7 – 3 = 4 (cm)

Bài 38 trang 84 SBT Toán 8 Tập 1: Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Chứng minh rằng DE // IK, DE = IK.

Lời giải:

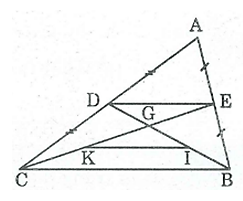
* Trong ΔABC, ta có:

E là trung điểm của AB và D là trung điểm của AC (giả thiết)

Nên ED là đường trung bình của ΔABC.

⇒ ED // BC và ED = $\frac{BC}{2}$ (tính chất đường trung bình của tam giác) (l)

* Trong ΔGBC, ta có:

I là trung điểm của BG và K là trung điểm của CG (gỉa thiết)

Nên IK là đường trung bình của ΔGBC.

⇒ IK // BC và $\frac{BC}{2}$ (tính chất đường trung bình của tam giác) (2)

Từ (l) và (2) suy ra: IK // DE, IK = DE.

Bài 39 trang 84 SBT Toán 8 Tập 1: Cho tam giác ABC, đường trung tuyến AM. Gọi D là trung điểm của AM, E là giao điểm của BD và AC. Chứng minh $A\text{}E\text{\hspace{0.17em}\hspace{0.17em}}=\frac{1}{2}\text{}EC$.

Lời giải:

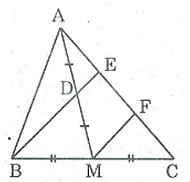
Gọi F là trung điểm của EC.

Trong ΔCBE, ta có:

M là trung điểm của CB;

F là trung điểm của CE.

Nên MF là đường trung bình của ΔCBE

⇒ MF // BE (tính chất đường trung bình của tam giác) hay DE // MF

* Trong ΔAMF, ta có: D là trung điểm của AM và DE // MF nên DE đi qua trung điểm của AF nên E là trung điểm AF

Suy ra: AE = EF (tính chất)

Mà EF = FC = $\frac{EC}{2}$ nên AE = $\frac{1}{2}\text{}EC$.

Bài 40 trang 84 SBT Toán 8 Tập 1: Cho tam giác ABC, các đường trung tuyến BD, CE. Gọi M, N theo thứ tự là trung điểm của BE, CD. Gọi I, K theo thứ tự là giao điểm của MN với BD, CE. Chứng minh MI = IK = KN.

Lời giải:

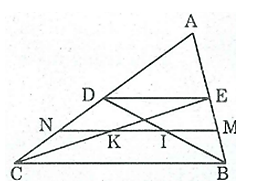
Trong ΔABC ta có: E là trung điểm của cạnh AB;

D là trung điểm của cạnh AC;

Nên ED là đường trung bình của Δ ABC.

⇒ ED // BC và ED = $\frac{1}{2}$BC.

(tính chất đường trung bình của tam giác)

+) Tứ giác BCDE có ED // BC nên BCDE là hình thang.

Trong hình thang BCDE, ta có: BC // DE

M là trung điểm cạnh bên BE

N là trung điểm cạnh bên CD

Nên MN là đường trung hình hình thang BCDE

⇒ MN // DE

$\begin{array}{l}MN\text{\hspace{0.17em}}=\frac{DE\text{\hspace{0.17em}\hspace{0.17em}}+BC\text{}}{2}\\ =\frac{\frac{BC}{2}\text{\hspace{0.17em}}+\text{}BC\text{}}{2}=\frac{3BC}{4}\end{array}$

(tính chất đường trung bình hình thang)

Trong ΔBED, ta có: M là trung điểm BE và MI // DE nên MI đi qua trung điểm của BD do đó I là trung điểm của BD

Suy ra: MI là đường trung bình của ΔBED

⇒ MI = $\frac{1}{2}$DE = $\frac{1}{4}$BC (tính chất đường trung bình của tam giác)

Trong ΔCED ta có: N là trung điểm CD và NK // DE nên NK đi qua trung điểm của CE do đó K là trung điểm của CE.

Suy ra: NK là đường trung bình của ΔCED.

⇒ NK =$\frac{1}{2}$ DE = $\frac{1}{4}$BC (tính chất đường trung bình của tam giác)

IK = MN – (MI + NK)

= $\frac{3}{4}$BC – ( $\frac{1}{4}$BC + $\frac{1}{4}$BC)

= $\frac{1}{4}$BC

⇒ MI = IK = KN = $\frac{1}{4}$BC.

Bài 41 trang 84 SBT Toán 8 Tập 1: Chứng minh rằng đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm của hai đường chéo và đi qua trung điểm của cạnh bên thứ hai.

Lời giải:

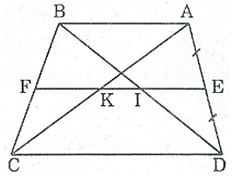
Giả sử ta có hình thang ABCD với E là trung điểm của AB và đường thẳng qua E song song với hai đáy AB, CD cắt BD, AC, BC lần lượt tại I, K  F.

Trong ΔADC ta có: E là trung điểm của cạnh AD và EK // DC (do EF song song với CD) do đó EK đi qua trung điểm của AC nên K là trung điểm AC

Trong ΔABD ta có: E là trung điểm của cạnh AD và EI // AB (do EF // AB) do đó EI đi qua trung điểm I của BD nên I là trung điểm của BD.

Trong tam giác ABC ta có: K là trung điểm của AC và FK song song với AB (do EF song song với AB) do đó FK đi qua trung điểm của BC nên F là trung điểm của BC.

Vậy đường thẳng song song với 2 đáy, đi qua trung điểm E của cạnh bên AD của hình thang ABCD thì đi qua trung điểm của cạnh bên BC và trung điểm hai đường chéo AC, BD.

Bài 42 trang 84 SBT Toán 8 Tập 1: Chứng minh rằng trong hình thang mà hai đáy không bằng nhau, đoạn thẳng nối trung điểm hai đường chéo bằng nửa hiệu của hai đáy.

Lời giải:

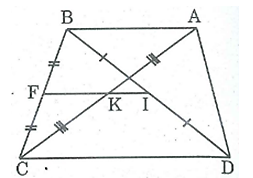
Giả sử hình thang ABCD có AB // CD, AB < CD.

Gọi I, K lần lượt là trung điểm hai đường chéo BD, AC; F là trung điểm của BC.

* Trong ΔACB, ta có:

K là trung điểm của cạnh AC

F là trung điểm của cạnh BC

Nên KF là đường trung bình của ΔACB

⇒ KF // AB và KF = $\frac{1}{2}$AB

(tính chất đường trung bình của tam giác)

Trong ΔBDC, ta có: I là trung điểm của cạnh BD

F là trung điểm của cạnh BC

Nên IF là đường trung bình của ΔBDC

⇒ IF // CD và IF = $\frac{1}{2}$CD (tính chất đường trung bình của tam giác)

FK // AB mà AB // CD nên FK // CD

Lại có: IF // CD (chứng minh trên)

Suy ra hai đường thẳng FI và FK trùng nhau.

⇒ I, K, F thẳng hàng, AB < CD

⇒ FK < FI nên K nằm giữa I và F

Ta có: IF = IK + KF

⇒ IK = IF – KF

= $\frac{1}{2}CD\text{\hspace{0.17em}\hspace{0.17em}}-\frac{1}{2}AB$

$\hspace{0.17em}=\frac{CD\text{\hspace{0.17em}\hspace{0.17em}}-AB}{2}$(điều phải chứng minh)

Bài 43 trang 85 SBT Toán 8 Tập 1: Hình thang ABCD có AB // CD; AB = a, BC = b, CD = c, DA = d. Các đường phân giác của góc ngoài đỉnh A và D cắt nhau tại M, các đường phân giác của các góc ngoài đỉnh B và C cắt nhau tại N.

a) Chứng minh rằng MN // CD.

b) Tính độ dài MN theo a, b, c, d (a. b, c, d có cùng đơn vị đo).

Lời giải:

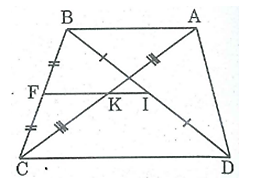
a) Gọi M' và N' là giao điểm của tia AM và BN với CD.

+ Ta có: $\widehat{M\text{'}}=\widehat{A_2}$ (sole trong)

$\widehat{A_1}=\widehat{A_2}$ (giả thiết)

⇒ $\widehat{M\text{'}}=\widehat{A_1}$ nên ΔADM' cân tại D

Vì DM là phân giác của $\widehat{ADM\text{'}}$.

Suy ra: DM là đường trung tuyến (tính chất tam giác cân)

⇒ AM = MM' nên M là trung điểm AM’

+ Ta có $\widehat{N\text{'}}=\widehat{B_2}$ (so le trong)

$\widehat{B_1}=\widehat{B_2}$ (giả thiết)

Vì $\widehat{N\text{'}}=\widehat{B_1}$ nên ΔBCN' cân tại C.

Lại có: CN là phân giác của $\widehat{BCN\text{'}}$

Suy ra: CN là đường trung tuyến (tính chất tam giác cân)

⇒ BN = NN' nên N là trung điểm BN’

Ta có N là trung điểm BN’; M là trung điểm AM’

Suy ra: MN là đường trung bình của hình thang ABN'M'

⇒ MN // M'N' (tính chất đường trung hình hình thang)

Hay MN // CD.

b) Ta có: $MN=\frac{AB+\text{\hspace{0.17em}}M\text{'}N\text{'}}{2}$ (tính chất đường trung hình hình thang).

$\Rightarrow MN=\frac{AB+\text{\hspace{0.17em}\hspace{0.17em}}M\text{'}D+\text{\hspace{0.17em}\hspace{0.17em}}CD+\text{\hspace{0.17em}}CN\text{'}}{2}$  (1)

Mà M'D = AD, CN' = BC.

Thay vào (1) :

$\begin{array}{l}\Rightarrow MN=\frac{AB+\text{\hspace{0.17em}\hspace{0.17em}}AD+\text{\hspace{0.17em}\hspace{0.17em}}CD+\text{\hspace{0.17em}}BC}{2}\\ =\frac{a+\text{\hspace{0.17em}}d+\text{\hspace{0.17em}}c+\text{\hspace{0.17em}}b}{2}\end{array}$

Bài 44 trang 85 SBT Toán 8 Tập 1: Cho tam giác ABC, đường trung tuyến AM. Gọi O là trung điểm của AM. Qua O kẻ đường thẳng d cắt các cạnh AB, AC. Gọi AA', BB', CC' là các đường vuông góc kể từ A, B, C đến đường thẳng d.

Chứng minh rằng: $\text{}AA\text{'}=\frac{BB\text{'}\text{\hspace{0.17em}\hspace{0.17em}}+CC\text{'}\text{\hspace{0.17em}}}{2}$

Lời giải:

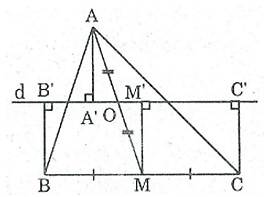
Ta có: BB' ⊥ d (giả thiết)

CC' ⊥ d (giả thiết)

Suy ra: BB'// CC'.

Tứ giác BB'C'C là hình thang

Kẻ MM' ⊥ d

⇒ MM' // BB' // CC' (quan hệ từ vuông góc đến song song)

Lại có M là trung điểm của BC nên M' là trung điểm của B’C’

⇒ MM' là đường trung bình của hình thang BB'C'C

⇒ $\text{}MM\text{'}=\frac{BB\text{'}\text{\hspace{0.17em}\hspace{0.17em}}+CC\text{'}\text{\hspace{0.17em}}}{2}$ (1)

* Xét hai tam giác vuông AA'O và MM'O:

$\widehat{AA\text{'}O}=\widehat{MM\text{'}O}$ = 90^o

AO = MO (giả thiết)

$\widehat{AOA\text{'}}=\widehat{MOM\text{'}}$ (2 góc đối đỉnh)

Do đó: ΔAA'O = ΔMM'O (cạnh huyền - góc nhọn)

⇒AA' = MM' (2)

Từ (1) và (2) suy ra:

$\text{}AA\text{'}=\frac{BB\text{'}\text{\hspace{0.17em}\hspace{0.17em}}+CC\text{'}\text{\hspace{0.17em}}}{2}$ (điều phải chứng minh).

Bài tập bổ sung

Bài 4.1 trang 85 SBT Toán 8 Tập 1: Trên hình bs.1, ta có AB // CD // EF // GH và AC = CE = EG. Biết CD = 9, GH = 13. Các độ dài AB và EF bằng...

Bài 4.2 trang 85 SBT Toán 8 Tập 1: Cho đường thẳng d và hai điểm A, B có khoảng cách đến đường thẳng d theo thứ tự là 20cm và 6cm...

Bài 4.3 trang 85 SBT Toán 8 Tập 1: Cho tam giác ABC. Gọi M là trung điểm của BC. Trên tia đối của tia BA lấy điểm D sao cho BD = AB...

Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:

Bài 5: Dựng hình bằng thước và compa. Dựng hình thang

Bài 6: Đối xứng trục

Bài 7: Hình bình hành

Bài 8: Đối xứng tâm

Bài 9: Hình chữ nhật

Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

Trắc nghiệm Đường trung bình của tam giác, của hình thang có đáp án