SBT Toán 8 Bài 2: Định lí đảo và hệ quả của định lí Ta-lét

Mục lục Giải SBT Toán 8 Bài 2: Định lí đảo và hệ quả của định lí Ta-lét

Bài 6 trang 84 SBT Toán 8 Tập 2: Cho tam giác ABC có cạnh BC = a. Trên cạnh AB lấy các điểm D và E sao cho AD = DE = EB. Từ D, E kẻ các đường thẳng song song với BC, cắt cạnh AC theo thứ tự tại M và N. Tính theo a độ dài các đoạn thẳng DM và EN.

Lời giải:

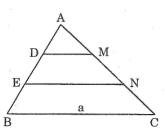
Ta có: AD = DE = EB =  $\frac{1}{3}\text{}AB$ (giả thiết)      (1)

Suy ra: AE = AD + DE  = $\frac{2}{3}AB$  (2)

Trong ΔABC, ta có: DM // BC (gt)

Nên $\frac{AD}{AB}=\frac{DM}{BC}$  (Hệ quả định lí Ta-lét)

Suy ra: $\frac{AD}{AB}=\frac{DM}{a}$    (3)

Từ (1) và (3) suy ra: $\frac{DM}{a}=\frac{1}{3}$

Suy ra: $DM=\frac{a}{3}$ .

Trong ΔABC, ta có: EN // BC (gt)

Suy ra: $\frac{AE}{AB}=\frac{EN}{BC}$( hệ quả định lí Ta- let).

Suy ra: $\frac{AE}{AB}=\frac{EN}{a}$ (4)

Từ (2) và (4) suy ra: $\frac{EN}{a}=\frac{2}{3}$  hay $EN=\frac{2a}{3}$ .

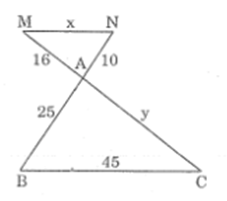
Bài 7 trang 84 SBT Toán 8 Tập 2: Cho hình vẽ bên

Cho biết MN // BC, AB = 25cm, BC = 45cm, AM = 16cm, AN = 10cm

Tính độ dài x, y của các đoạn thẳng MN, AC.

Lời giải:

Ta có: MN // BC (gt), áp dụng hệ quả của định lý Ta – lét  

Suy ra:  $\frac{AN}{AB}=\frac{AM}{AC}=\frac{MN}{BC}$ (Hệ quả định lí Ta-lét)

$\begin{array}{l}\iff \frac{10}{25}=\frac{16}{y}=\frac{x}{45}\\ \Rightarrow x=45.\frac{10}{25}=18;\\ \hspace{0.17em}y=16.\frac{25}{10}=40\end{array}$

Vậy x = 18; y = 40.

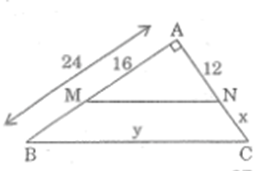
Bài 8 trang 84 SBT Toán 8 Tập 2: Hình vẽ cho biết tam giác ABC vuông tại A, MN // BC, AB = 24cm, AM = 16cm, AN = 12cm. Tính độ dài x, y của các đoạn thẳng NC, BC.

Lời giải:

Trong ΔABC, ta có: MN // BC (gt)

Suy ra: $\frac{AM}{AB}=\frac{AN}{AC}$ (định lí Ta- let)

Suy ra: $AC=\frac{AB.AN}{AM}=\frac{24.12}{16}=18\left(cm\right)$

Vậy NC = AC – AN = 18 – 12 = 6(cm)

Áp dụng định lí Pi-ta-go vào tam giác vuông AMN, ta có:

MN² = AM² + AN² = 16² + 12² = 400

MN = 20cm

Trong ΔABC, ta có: MN // BC (gt)

Suy ra: $\frac{AM}{AB}=\frac{MN}{BC}$ (Hệ quả định lí Ta – lét).

Vậy: $BC\text{\hspace{0.17em}\hspace{0.17em}}=\frac{MN.AB}{AM}=\frac{20.24}{16}=30\left(cm\right)$.

Vậy x = NC = 6 cm, y = BC = 30 cm.

Bài 9 trang 84 SBT Toán 8 Tập 2: Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O.

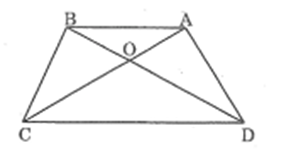
Chứng minh rằng: OA.OD = OB.OC.

Lời giải:

Ta có: AB // CD (gt), áp dụng hệ quả của định lý Ta – lét 

Suy ra $\frac{OA}{OC}=\frac{OB}{OD}$ (hệ quả định lí ta-lét)

Vậy OA.OD = OB.OC (điều phải chứng minh).

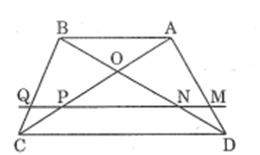
Bài 10 trang 84 SBT Toán 8 Tập 2: Cho hình thang ABCD (AB // CD). Đường thẳng song song với đáy AB cắt các cạnh bên và các đường chéo AD, BD, AC, và BC theo thứ tự các điểm M, N, P, Q. Chứng minh rằng MN = PQ.

Lời giải:

Trong ΔADB, ta có: MN // AB (gt)

Suy ra: $\frac{DN}{DB}=\frac{MN}{AB}$  (hệ quả định lí ta-lét) (1)

Trong ΔACB, ta có: PQ // AB (gt)

Suy ra: $\frac{CQ}{CB}=\frac{PQ}{AB}$  (Hệ quả định lí Ta-lét) (2)

Lại có: NQ // AB (gt) và AB // CD (gt)

Suy ra: NQ // CD.

Trong ΔBDC, ta có: NQ // CD (chứng minh trên)

Suy ra: $\frac{DN}{DB}=\frac{CQ}{CB}$ (Định lí Ta-lét) (3)

Từ (1), (2) và (3) suy ra $\frac{MN}{AB}=\frac{PQ}{AB}$ hay MN = PQ (điều phải chứng minh).

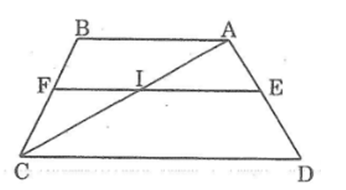
Bài 11 trang 85 SBT Toán 8 Tập 2: Cho hình thang ABCD (AB // CD). Trên cạnh AD lấy điểm E sao cho $\frac{AE}{ED}=\frac{p}{q}$. Qua E kẻ đường thẳng song song với các đáy và cắt BC tại F. Chứng minh rằng: $E\text{}F=\frac{p.CD+q.AB}{p+\text{\hspace{0.17em}}q}$ .

Lời giải:

Kẻ đường chéo AC cắt EF tại I.

Trong ΔADC, ta có: EI // CD

Suy ra: $\frac{AE}{AD}=\frac{EI}{CD}$

Suy ra: $EI=\frac{AE}{AD}.CD\left(1\right)$  

Lại có: $\frac{AE}{ED}=\frac{p}{q}$ (giả thiết)

Suy ra: $\frac{AE}{AD}=\frac{AE}{AE+\text{\hspace{0.17em}\hspace{0.17em}}ED}=\frac{p}{q+p}\left(2\right)$

Từ (1) và (2) suy ra: $EI=\frac{p}{p+\text{}q}.CD$ .

Trong ΔABC, ta có: FI // AB

Suy ra: $\frac{BF}{FC}=\frac{AI}{IC}$ (định lí ta-lét) (3)

Trong ΔADC, ta có : EI // CD

Suy ra: $\frac{AE}{ED}=\frac{AI}{IC}$ (định lí ta-lét) (4)

Từ (3) và (4) suy ra $\frac{BF}{FC}=\frac{AE}{ED}=\frac{p}{q}$

Trong ΔABC, ta có: IF // AB

Suy ra: $\text{}\frac{IF}{AB}=\frac{CF}{CB}$  (định lí ta-lét)

Suy ra: $\text{}I\text{}F=\frac{CF}{CB}.AB$  ( 5)

Ta có: $\frac{BF}{C\text{}F}=\frac{p}{q}$ ( chứng minh trên)

Suy ra: 

$$\begin{gathered} \frac{CF\text{}}{B\text{}F}=\frac{q}{p}\Rightarrow \frac{CF\text{}}{C\text{}F+BF}=\frac{q}{p+q} \\ \Rightarrow \frac{CF\text{}}{BC}=\frac{q}{p+q}\text{ (6)} \end{gathered}$$

Từ (5) và (6) suy ra: $\text{}IF=\frac{q}{p+\text{}q}AB$

Vậy: 

$$\begin{gathered} E\text{}F=EI+IF \\ =\frac{p}{p+\text{}q}.CD+\text{\hspace{0.17em}}\frac{q}{p+\text{}q}.AB \\ =\frac{p.CD+\text{}qAB}{p+\text{}q} \end{gathered}$$

(điều phải chứng minh).

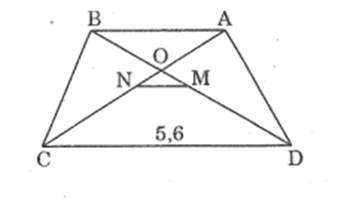
Bài 12 trang 85 SBT Toán 8 Tập 2: Hình thang cân ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O. Gọi M, N theo thứ tự là trung điểm của BD và AC. Cho biết MD = 3MO, đáy lớn CD = 5,6cm

a) Tính độ dài đoạn thẳng MN và đáy nhỏ AB.

b) So sánh độ dài đoạn thẳng MN với nửa hiệu của CD và AB.

Lời giải:

a) Vì ABCD là hình thang cân có AB // CD nên:

AC = BD (1)

Xét ΔADC và ΔBCD, ta có:

AC = BD (chứng minh trên)

AD = BC (hình thang ABCD cân)

CD cạnh chung

Suy ra: ΔADC = ΔBCD (c.c.c)

Suy ra: $\widehat{ACD}=\widehat{BDC}$

Hay $\widehat{OCD}=\widehat{ODC}$

Suy ra tam giác OCD cân tại O

Suy ra: OD = OC (tính chất tam giác cân) (2)

Từ (1) và (2) suy ra: OA = OB

Ta có: $AN=BM=\frac{1}{2}AC=\frac{1}{2}BD$

Mà OA = OB ⇒ OM = ON

Lại có: MD = 3MO (gt) ⇒ NC = 3NO

Trong ΔOCD, ta có: $\frac{MO}{MD}=\frac{NO}{NC}=\frac{1}{3}$

Suy ra: MN // CD (Định lí đảo của định lí Ta-lét)

Ta có: OD = OM + MD = OM + 3OM = 4OM

Trong ΔOCD, ta có: MN // CD

Suy ra: $\frac{OM}{OD}=\frac{MN}{CD}$  (Hệ quả định lí Ta-lét)

Suy ra: $\frac{MN}{CD}=\frac{OM}{4OM}=\frac{1}{4}$

Suy ra: MN = $\frac{1}{4}$CD = $\frac{1}{4}$.5,6 = 1,4 (cm).

Ta có: MB = MD (gt)

Suy ra: MB = 3OM hay OB = 2OM

Lại có: AB // CD (gt), MN //CD suy ra: MN // AB

Ta có: MN // AB, áp dụng hệ quả định lý Ta – let ta được: $\frac{OM}{OB}=\frac{MN}{AB}$ (Hệ quả định lí Ta-lét)

Suy ra:  $\frac{MN}{AB}=\frac{OM}{2OM}=\frac{1}{2}$.

Vậy: AB = 2MN = 2.1,4 = 2,8(cm).

b) Ta có: $\frac{CD\text{}-AB}{2}=\frac{5,6-2,8}{2}=1,4cm$

Mà MN = 1,4 cm

Vậy  $MN\text{}=\frac{CD-AB}{2}$.

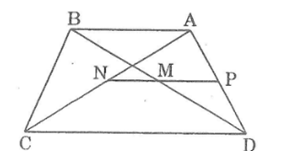
Bài 13 trang 85 SBT Toán 8 Tập 2: Cho hình thang ABCD (AB // CD, AB < CD). Gọi trung điểm các đường chéo AC, BD thứ tự là N và M. Chứng minh rằng:

a) MN // AB;

b) $MN=\frac{CD-AB}{2}$.

Lời giải:

a) Gọi P là trung điểm của AD, nối PM

Trong ΔDAB ta có: $\frac{PA}{AD}=\frac{1}{2};\frac{BM}{BD}=\frac{1}{2}$

Suy ra: $\frac{PA}{AD}=\frac{BM}{BD}$ .

Suy ra: PM // AB (Định lí đảo của định lí Ta-lét) (1)

Trong ΔACD, ta có $\frac{AP}{AD}=\frac{1}{2};\frac{AN}{AC}=\frac{1}{2}$

Suy ra: $\frac{AP}{AD}=\frac{AN}{AC}$.

Suy ra: PN // CD (định lí đảo định lí Ta-lét) (2)

Lại có AB // CD (gt) (3)

Từ (1), (2) và (3) và theo tiên đề Ơ-clít suy ra P, M, N thẳng hàng.

Vậy MN // CD hay MN // AB.

b) Vì PM là đường trung bình của tam giác DAB nên:

 $PM=\frac{AB}{2}$ (tính chất đường trung bình tam giác)

Vì PN là đường trung bình của tam giác ΔACD nên:

$PN=\frac{CD}{2}$ (tính chất đường trung hình tam giác)

Mà PN = PM + MN

Suy ra: $MN=PN-PM=\frac{CD}{2}-\frac{AB}{2}=\frac{CD\text{}-\text{}AB}{2}$ (điều phải chứng minh).

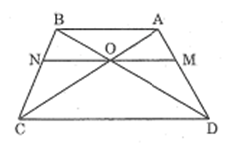
Bài 14 trang 85 SBT Toán 8 Tập 2: Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M, N. Chứng minh rằng OM = ON.

Lời giải:

Trong ΔDAB, ta có: OM // AB (gt)

$\Rightarrow \frac{OM}{AB}=\frac{DO}{DB}$ (Hệ quả định lí Ta-lét) (1)

Trong ΔCAB, ta có: ON // AB (gt)

$\Rightarrow \frac{ON}{AB}=\frac{CN}{CB}$ (Hệ quả định lí Ta-lét) (2)

Trong ΔBCD, ta có: ON // CD (gt)

Suy ra: $\frac{DO}{DB}=\frac{CN}{CB}$ (định lí Ta-lét) (3)

Từ (1), (2) và (3) suy ra: $\frac{OM}{AB}=\frac{ON}{AB}$

Vậy: OM = ON  ( điều phải chứng minh).

Bài 15 trang 86 SBT Toán 8 Tập 2: Cho trước ba đoạn thẳng có độ dài tương ứng là m, n, p. Hãy dựng đoạn thẳng thứ tư có độ dài là q sao cho $\frac{m}{n}=\frac{p}{q}$ .

Lời giải:

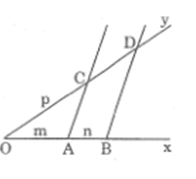
* Cách dựng:

- Dựng hai tia chung gốc Ox và Oy phân biệt không đối nhau.

- Trên tia Ox dựng đoạn OA = m và dựng đoạn AB = n sao cho A nằm giữa O và B

- Trên tia Oy dựng đoạn OC = p.

- Dựng đường thẳng AC

- Từ B dựng đường thẳng song song với AC cắt tia Oy tại D.

Đoạn thẳng CD = q cần dựng.

* Chứng minh:

Theo cách dựng, ta có: AC // BD.

Trong ΔOBD ta có: AC // BD.

Suy ra: $\frac{OA}{AB}=\frac{OC}{CD}$  ( định lí Ta- let).

Vậy $\frac{m}{n}=\frac{p}{q}$.

Bài 16 trang 86 SBT Toán 8 Tập 2: Cho đoạn thẳng AB = 3cm, CD = 5cm, EF = 2cm. Hãy dựng đoạn thẳng thứ tư có độ dài là a sao cho $\frac{AB}{CD}=\frac{E\text{}F}{a}$ hay $\frac{3}{5}=\frac{2}{a}$. Tính giá trị của a

Lời giải:

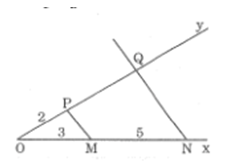
* Cách dựng:

- Dựng hai tia chung gốc Ox và Oy phân biệt không đối nhau.

- Trên Ox dựng đoạn OM = AB = 3cm

và dựng đoạn MN = CD = 5cm sao cho M nằm giữa O và N

- Trên tia Oy dựng đoạn OP = EF = 2cm.

- Dựng đường thẳng PM.

- Từ N dựng đường thẳng song song với PM cắt tia Oy tại Q.

Đoạn thẳng PQ = a cần dựng..

* Chứng minh:

Theo cách dựng, ta có: PM // NQ.

Trong ΔONQ ta có: PM // NQ.

Suy ra: $\frac{OM}{MN}=\frac{OP}{PQ}$( định lí Ta- let).

Suy ra: $\frac{AB}{CD}=\frac{EF}{a}$ hay $\frac{3}{5}=\frac{2}{a}$

Vậy $a=\frac{5.2}{3}=\frac{10}{3}$ cm.

Bài tập bổ sung

Bài 2.1 trang 86 SBT Toán 8 Tập 2: Hình bs.1 cho biết AB // CD, O ∈ MN, MN = 5cm, OB = 1,5cm, OD = 4,5cm, MB = 1cm...

Bài 2.2 trang 86 SBT Toán 8 Tập 2: Tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại O. Chứng minh rằng OM.OC = ON.OB...

Bài 2.3 trang 86 SBT Toán 8 Tập 2: Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O...

Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:

Bài 3: Tính chất đường phân giác của tam giác

Bài 4: Khái niệm hai tam giác đồng dạng

Bài 5: Trường hợp đồng dạng thứ nhất (c.c.c)

Bài 6: Trường hợp đồng dạng thứ hai (c.g.c)

Bài 7: Trường hợp đồng dạng thứ ba (g.g)

Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

Lý thuyết Định lí đảo và hệ quả của định lí Ta - lét

Trắc nghiệm Định lý đảo và hệ quả của định lý Ta-let có đáp án