Nội dung bài viết

    Xem thêm

    SBT Toán 8 Bài 8: Các trường hợp đồng dạng của tam giác vuông

    Với giải sách bài tập Toán lớp 8 Bài 8: Các trường hợp đồng dạng của tam giác vuông chi tiết được Giáo viên nhiều năm kinh nghiệm biên soạn bám sát nội dung sách bài tập Toán 8 Tập 2 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. 

    1 1,520 19/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Mục lục Giải SBT Toán 8 Bài 8: Các trường hợp đồng dạng của tam giác vuông

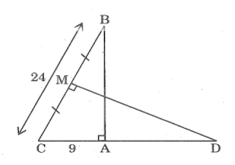
    Bài 44 trang 95 SBT Toán 8 Tập 2: Cho tam giác ABC vuông tại A, AC = 9cm, BC = 24cm. Đường trung trực của BC cắt đường thẳng AC tại D, cắt BC tại M. Tính độ dài của đoạn thẳng CD.

    Tài liệu VietJack

    Lời giải:

    Xét hai tam giác vuông ABC và MDC, ta có:

    BAC^=DMC^=90°

    C^ chung

    Suy ra tam giác ABC đồng dạng với tam giác MDC (g.g)

    Suy ra: ACMC  = BCDC 

    Suy ra: DC=  MC.  BCAC

    Ta có: MC = 12.BC = 12.24 = 12 (cm)

    Vây DC = 12.249  =32 (cm).

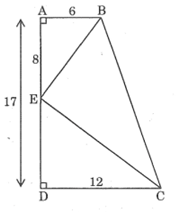
    Bài 45 trang 95 SBT Toán 8 Tập 2: Cho hình thang vuông ABCD ( A^=D^=90°); AB = 6cm, CD = 12cm, AD = 17cm. Trên cạnh AD, đặt đoạn AE = 8cm. Chứng minh BEC^ =90°.

    Tài liệu VietJack

    Lời giải:

    Ta có: AD = AE + DE

    Suy ra: DE = AD – AE = 17 – 8 = 9cm

    Xét ΔABE và ΔDEC, ta có:

     A^=D^ = 90o (1)

    Mà : ABDE  =  69  =  23; AEDC =  812  =  23

    Suy ra: ABDE  =  AEDC  (2)

    Từ (1) và (2) suy ra :ΔABE đồng dạng ΔDEC (c.g.c)

    Suy ra: ABE^=DEC^ 

    Trong ΔABE ta có: A^ = 90o 

    ⇒ AEB^+ABE^=90° 

    Suy ra: AEB^+DEC^ = 90o

    Lại có: AEB^+BEC^+DEC^=AED^=180°

    Vậy : BEC^ = 180o - AEB^+DEC^

    = 180o - 90o = 90o

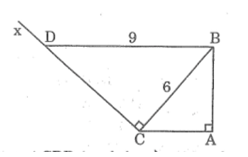
    Bài 46 trang 95 SBT Toán 8 Tập 2: Cho tam giác ABC vuông tại A, AC = 4cm, BC = 6cm. Kẻ tia Cx vuông góc với BC (tia Cx và điểm A khác phía so với đường thẳng BC). Lấy trên Cx điểm D sao cho BD = 9cm. Chứng minh rằng BD // AC.

    Tài liệu VietJack

    Lời giải:

    Xét hai tam giác vuông ABC và CDB, ta có:

     BAC^=DCB^ = 90o (1)

    Mà: ACCB  =  46  =  23;  CBBD  =  69  =  23 .

    Suy ra: ACCB  = CBBD  (2).

    Từ (1) và (2) suy ra: ΔABC đồng dạng ΔCDB (cạnh huyền và cạnh góc vuông tỉ lệ)

    Suy ra: ACB^=CBD^

    ⇒ BD // AC ( hai góc ở vị trí so le trong bằng nhau).

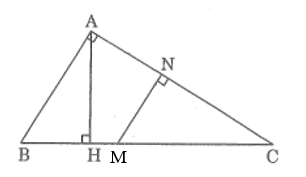
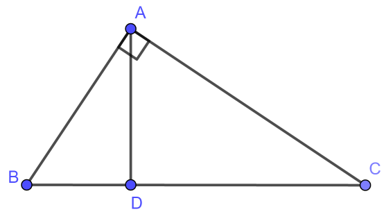
    Bài 47 trang 95 SBT Toán 8 Tập 2: Trên hình vẽ hãy chỉ ra các tam giác đồng dạng. Viết các cặp tam giác đồng dạng theo thứ tự các đỉnh tương ứng và giải thích vì sao chúng đồng dạng.

    Tài liệu VietJack

    Lời giải:

    - ΔABC đồng dạng ΔHBA

    Vì hai tam giác vuông có góc nhọn ở đỉnh B chung.

    - ΔABC đồng dạng ΔHAC

    Vì hai tam giác vuông có góc nhọn ở đỉnh C chung

    - ΔABC đồng dạng ΔNMC

    Vì hai tam giác vuông có góc nhọn ở đỉnh C chung

    - ΔHAC đồng dạng ΔNMC

    Vì hai tam giác vuông có góc nhọn ở đỉnh C chung

    - ΔHAC đồng dạng ΔHBA

    Vì hai tam giác vuông có góc nhọn HBA^=HAC^ (cùng phụ với BAH^)

    - ΔHAB đồng dạng ΔNCM

    Vì hai tam giác vuông có góc nhọn HAB^=NCM^ (cùng phụ với HAC^)

    Bài 48 trang 95 SBT Toán 8 Tập 2: Cho tam giác ABC ( A^ = 90o) có đường cao AH. Chứng minh rằng AH2 = BH.CH.

    Lời giải:

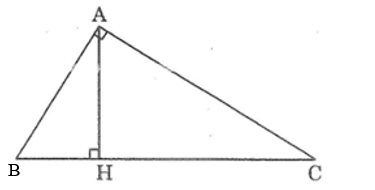
    Tài liệu VietJack

    Xét hai tam giác vuông HBA và HAC, ta có:

    AHB^=AHC^=90°

     B^=HAC^ (hai góc cùng phụ C^)

    Suy ra: ΔHBA đồng dạng ΔHAC (g.g)

    Suy ra: HAHB  =  HCHA

    Vậy AH2 = BH.CH  (điều phải chứng minh).

    Bài 49 trang 96 SBT Toán 8 Tập 2: Đường cao của một tam giác vuông xuất phát từ đỉnh góc vuông chia cạnh huyền thành hai đoạn thẳng có dộ dài là 9cm và 16cm. Tính độ dài các cạnh của tam giác vuông.

    Tài liệu VietJack

    Lời giải:

    Xét hai tam giác vuông DAC và DBA ,ta có:

    ADC^=BDA^ = 90o

    C^=DAB^  (hai góc cùng phụ B^)

    Suy ra: ΔDAC đồng dạng ΔDBA (g.g)

    Suy ra:  DBDA= DADC  =  ABAC

    ⇒ DA2 = DB.DC

    hay DA​=  DB.  DC  =  9.16  =12(cm).

    Áp dụng định lí Pi-ta-go vào tam giác vuông ABD, ta có:

    AB2 = DA2 + DB2 = 92 + 122 = 225 ⇒ AB =15 (cm)

    Áp dụng định lí Pi-ta-go vào tam giác vuông ACD,ta có:

    AC2 = DA2 + DC2 = 122 +162 = 400 ⇒ AC = 20cm

    Vậy BC = BD + DC = 9 + 16 = 25(cm).

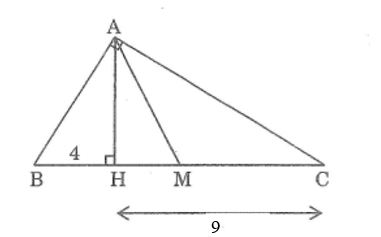
    Bài 50 trang 96 SBT Toán 8 Tập 2: Tam giác vuông ABC ( A^ = 90o) có đường cao AH và trung tuyến AM. Tính diện tích tam giác AMH, biết rằng BH = 4cm, CH = 9cm

    Tài liệu VietJack

    Lời giải:

    Xét hai tam giác vuông HBA và HAC có:

    BHA^=AHC^ = 90o

    B^=HAC^ (hai góc cùng phụ C^)

    Do đó: ΔHBA đồng dạng ΔHAC (g.g)

    Suy ra: HAHB  =  HCHA 

    ⇒ HA2 = HB.HC = 4.9 = 36(cm)

    Suy ra: AH = 6 (cm)

    Lại có: BM = 12BC = 12.(9 + 4) =  12.13 = 6,5cm

    Mà HM = BM – BH = 6,5 – 4 = 2,5cm

    Vậy SAHM = 12.AH.HM =  12.6.2,5 = 7,5cm2

    Bài tập bổ sung

    Bài 8.1 trang 96 SBT Toán 8 Tập 2: Cho góc nhọn xOy. Trên tia Ox lấy một điểm A sao cho OA = 8,65cm...

    Bài 8.2 trang 96 SBT Toán 8 Tập 2: Tam giác ABC vuông tại A có đường cao AH = n = 10,85cm và cạnh AB = m = 12,5cm...

    Bài 8.3 trang 96 SBT Toán 8 Tập 2: Cho tam giác ABC vuông tại A, chân H của đường cao AH chia cạnh huyền BC thành hai đoạn...

    Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:

    Ôn tập chương 3 - Hình học

    Bài 1: Hình hộp chữ nhật

    Bài 2: Hình hộp chữ nhật (tiếp)

    Bài 3: Thể tích của hình hộp chữ nhật

    Bài 4: Hình lăng trụ đứng

    Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

    Lý thuyết Các trường hợp đồng dạng của tam giác vuông

    Trắc nghiệm Trường hợp đồng dạng của tam giác vuông có đáp án

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,520 19/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: