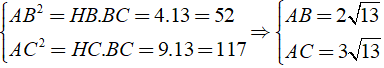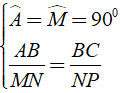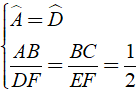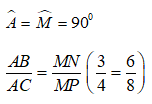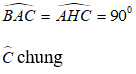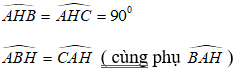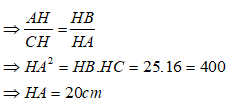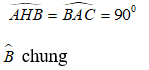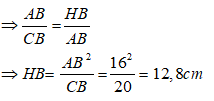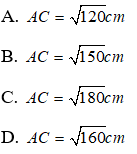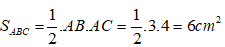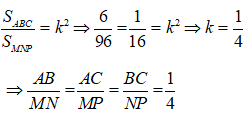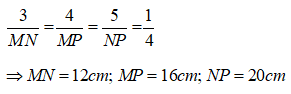TOP 40 câu Trắc nghiệm Trường hợp đồng dạng của tam giác vuông (có đáp án 2023) - Toán 8

Trắc nghiệm Toán 8 Bài 8: Trường hợp đồng dạng của tam giác vuông

Bài giảng Trắc nghiệm Toán 8 Bài 8: Trường hợp đồng dạng của tam giác vuông

Bài 1: Cho tam giác ABC cân tại A. Đường thẳng qua C và vuông góc AB tại CE. Tính AB, biết BC = 18cm và BE = 6,75cm.

A. 16cm

B. 32cm

C. 24cm

D. 18cm

Hiển thị đáp án  

Đáp án: C

Giải thích:

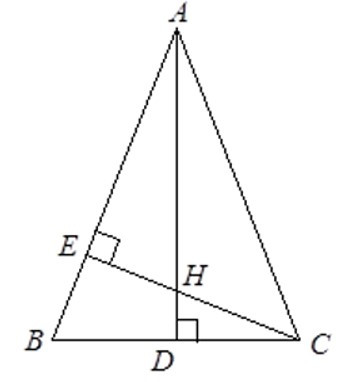
Kẻ đường cao AD.

Xét ΔCBE và ΔABD có

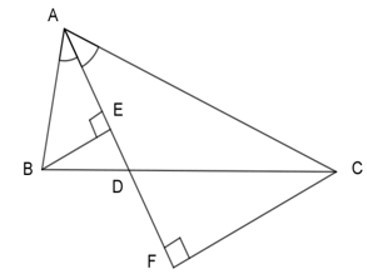
Bài 2: Cho tam giác ABC, phân giác AD. Gọi E, F lần lượt là hình chiếu của B và C lên AD. Chọn khẳng định không đúng.

A. AE.CF = AF.BE

B. AE.DF = ED²

C. AE.DF = AF.DE

D. $\frac{BE}{CF}=\frac{DE}{DF}$ 

Hiển thị đáp án  

Đáp án: B

Giải thích:

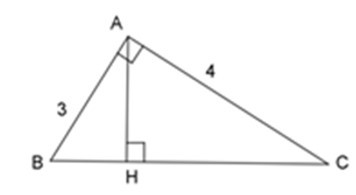
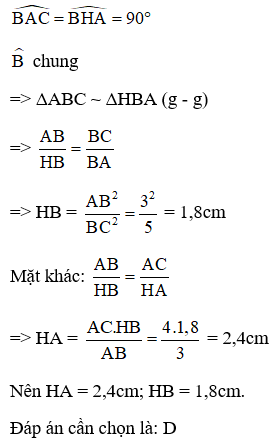
Bài 3: Tam giác ABC vuông tại A có đường cao AH. Cho biết AB = 3cm; AC = 4cm. Tính độ dài các đoạn thẳng HA, HB.

A. HA = 2,4cm; HB = 1,2cm

B. HA = 2cm; HB = 1,8cm

B. HA = 2cm; HB = 1,2cm

D. HA = 2,4cm; HB = 1,8cm

Hiển thị đáp án  

Đáp án: D

Giải thích:

Bài 4: Cho tam giác ABC vuông tại A, đường cao AH chia cạnh BC thành hai đoạn thẳng HB = 7cm và HC = 18cm. Điểm E thuộc đoạn thẳng HC sao cho đường thẳng  đi qua E và vuông góc với BC chia tam giác ABC thành hai phần có diện tích bằng nhau. Tính CE.

A. 15cm

B. 12cm

C. 10cm

D. 8cm

Hiển thị đáp án  

Đáp án: A

Giải thích:

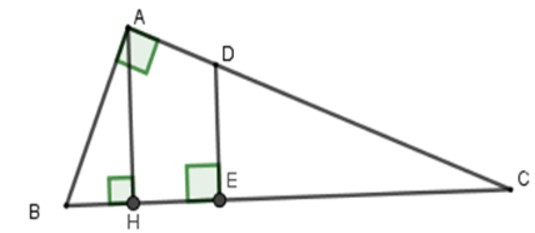
Gọi D là giao điểm của AC và đường vuông góc với BC tại E.

Xét ΔAHC và ΔABC có C chung và AHC^ = BAC^ = 90⁰ nên ΔAHC ~ ΔBAC (g-g)

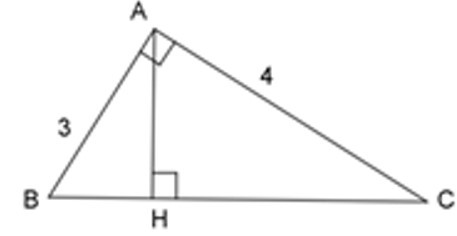
Bài 5: Tam giác ABC vuông tại A có đường cao AH. Cho biết AB = 3cm; AC = 4cm. Chọn kết luận không đúng.

A. HA = 2,4cm

B. HB = 1,8cm

C. HC = 3,2cm

D. BC = 6cm

Hiển thị đáp án  

Đáp án: D

Giải thích:

Bài 6: Cho các mệnh đề sau. Chọn câu đúng.

(I) Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.

(II) Nếu một góc của tam giác vuông này lớn hơn một góc của tam giác vuông kia thì hai tam giác vuông đó đồng dạng

A. (I) đúng, (II) sai

B. (I) sai, (II) đúng

C. (I) và (II) đều sai

D. (I) và (II) đều đúng

Hiển thị đáp án  

Đáp án: A

Giải thích:

Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.

Vậy (I) đúng, (II) sai

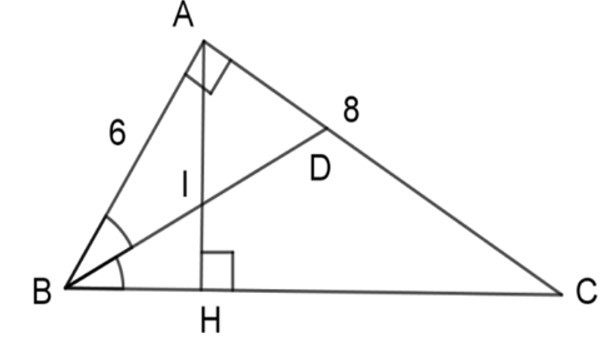
Bài 7: Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm, đường cao AH, đường phân giác BD. Gọi I là giao điểm của AH và BD.

1. Chọn kết luận đúng.

A. AD = 6cm

B. DC = 5cm

C. AD = 5cm

D. BC = 12cm

Hiển thị đáp án  

Đáp án: B

Giải thích:

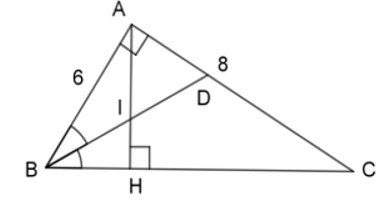
+ Áp dụng định lý Pitago trong tam giác vuông ABC ta có:

AB² + AC² = BC² $\iff$ 6² + 8² = BC²

$\iff$ BC² = 100 => BC = 10cm

+ Vì BD là đường phân giác của tam giác ABC nên áp dụng tính chất đường phân giác của tam giác, ta có:

$$\begin{gathered} \frac{BA}{AD}=\frac{BC}{CD} \\ \iff \frac{BA}{AD}=\frac{BC}{CA-AD} \\ \iff \frac{6}{AD}=\frac{10}{8-AD} \end{gathered}$$

=> AD = 3cm

=> DC = AC - AD = 8 - 3 = 5cm

2. Chọn khẳng định đúng.

A. AB.BI = BD.HB

B. AB.BI = AI²

B. AB.BI = BD²

D. AB.BI = HI²

Hiển thị đáp án  

Đáp án: A

Giải thích:

Bài 8: Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 3,5cm và HC = 9cm. Điểm E thuộc đoạn thẳng HC sao cho đường thẳng đi qua E và vuông góc với BC chia tam giác ABC thành hai phần có diện tích bằng nhau. Tính CE.

A. 10cm

B. 6cm

C. 5cm

D. 7,5cm

Hiển thị đáp án  

Đáp án: D

Giải thích:

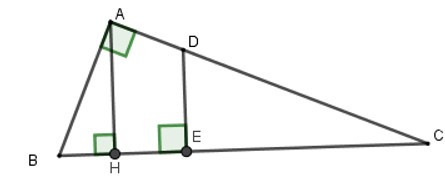
Gọi D là giao điểm của AC và đường vuông góc với BC tại E.

Xét ΔAHC và ΔABC có C chung và AHC^ = BAC^ = 90⁰ nên ΔAHC ~ ΔBAC (g-g)

Bài 9: Cho hai tam giác vuông. Điều kiện để hai tam giác vuông đó đồng dạng là:

A. Có hai cạnh huyền bằng nhau

B. có 1 cặp cạnh góc vuông bằng nhau

C. Có hai góc nhọn bằng nhau

D. không cần điều kiện gì

Hiển thị đáp án  

Đáp án: C

Giải thích:

Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.

Bài 10: Cho hình vẽ dưới đây với $\widehat{BAH }=\widehat{ACH}$.

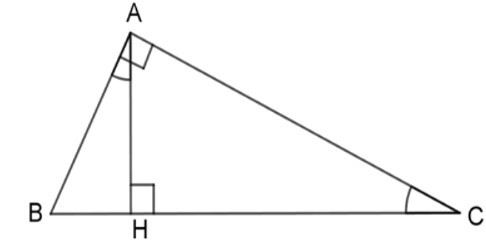
Khi đó các mệnh đề

(I) ΔAHB ~ ΔCHA (g - g)

(II) ΔAHC ~ ΔBAC (g - g)

A. (I) đúng

B. (II) đúng

C. Cả (I) và (II) đều sai

D. Cả (I) và (II) đều đúng

Hiển thị đáp án  

Đáp án: D

Giải thích:

Xét 2 tam giác vuông AHB và CHA có: BAH^ = ACH^ (gt)

=> ΔAHB ~ ΔCHA (g - g)

=> (I) đúng

Xét 2 tam giác vuông AHC và BAC có:

C chung

=> ΔAHC ~ ΔBAC (g - g)

=> (II) đúng

Vậy cả (I) và (II) đều đúng.

Bài 11: Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm, đường cao AH, đường phân giác BD.

1. Tính độ dài các đoạn AD, DC lần lượt là

A. 6cm, 4cm

B. 2cm, 5cm

C. 5cm, 3cm

D. 3cm, 5cm

Hiển thị đáp án  

Đáp án: D

Giải thích:

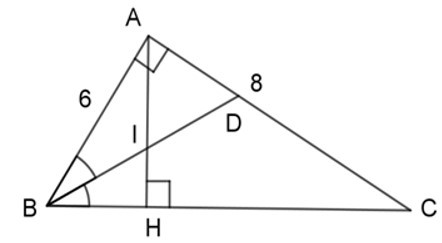
2. Gọi I là giao điểm của AH và BD. Chọn câu đúng.

A. AB.BI = BD.HB

B. AB.BI = AI²

C. AB.BI = BD²

D. AB.BI = HI²

Hiển thị đáp án  

Đáp án: A

Giải thích:

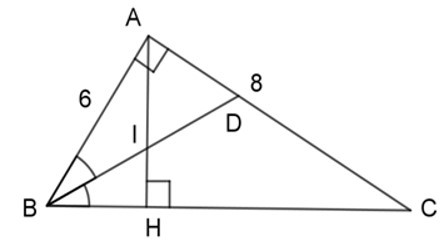
Xét 2 tam giác vuông ABD và HBI có:

Bài 12: Cho hình vẽ dưới đây với $\widehat{BAH }=\widehat{ACH}$ .

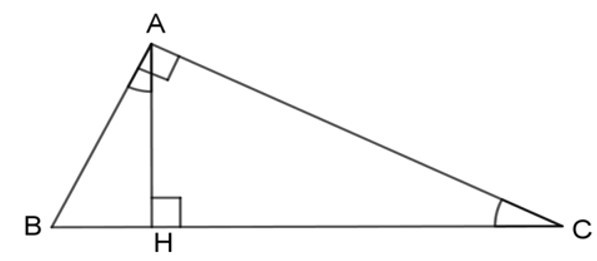
Chọn mệnh đề sai:

A. ΔAHB ~ ΔCHA

B. ΔBAH ~ ΔBCA

C. ΔBAH ~ ΔCBA

D. ΔAHC ~ ΔBAC

Hiển thị đáp án  

Đáp án: C

Giải thích:

Xét 2 tam giác vuông AHB và CHA có: $\widehat{BAH}=\widehat{ACH}$ (gt)

=> ΔAHB ~ ΔCHA (g - g)

=> A đúng

Xét 2 tam giác vuông AHC và BAC có:

Góc C chung

=> ΔAHC ~ ΔBAC (g - g)

=> D đúng

Xét hai tam giác vuông BAH và BCA có:

Góc B chung

$\widehat{BAH}=\widehat{ACH}$ (gt)

=> ΔBAH ~ ΔBCA (g - g) nên B đúng, C sai.

Bài 13: Cho tam giác ABC cân tại A, AC = 20cm, BC = 24cm, các đường cao AD và CE cắt nhau ở H. Độ dài AH là:

A. 12cm

B. 7cm

C. 9cm

D. 10cm

Hiển thị đáp án  

Đáp án: B

Giải thích:

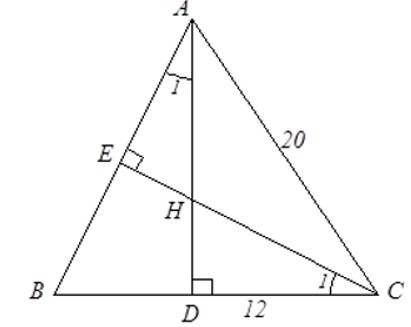
Bài 14: Cho ΔABC ~ ΔDHE với tỉ số đồng dạng $\frac{2}{3}$. Tỉ số hai đường cao tương ứng của ΔDHE và ΔABC là:

A.$\frac{2}{3}$

B.$\frac{3}{2}$

C.$\frac{4}{9}$

D. 1

Hiển thị đáp án  

Đáp án: B

Giải thích:

Vì ΔABC ~ ΔDHE với tỉ số đồng dạng $\frac{2}{3}$ nên tỉ số đồng dạng của hai tam giác DHE và ABC là $\frac{3}{2}$ .

Vậy tỉ số hai đường cao tương ứng của ΔDHE và ΔABC là $\frac{3}{2}$

Bài 15: Với giả thiết được cho trong hình, kết quả nào sau đây là đúng?

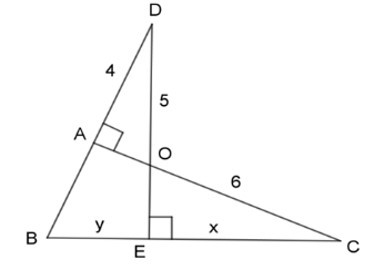
A. y = 10

B. x = 4,8

C. x = 5

D. y = 8,25

Hiển thị đáp án  

Đáp án: B

Giải thích:

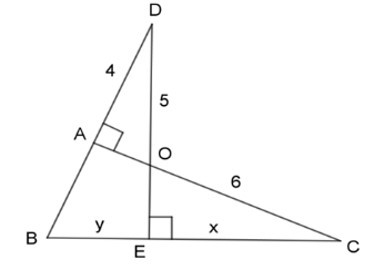
Xét 2 tam giác vuông ΔADO(DAO = 90⁰) và ΔECO (CEO = 90⁰) ta có:

 $\widehat{AOD}=\widehat{EOC}$(2 góc đối đỉnh)

=> ΔADO ~ ΔECO (g.g)

$$\begin{gathered} \Rightarrow \frac{AD}{EC}=\frac{DO}{CO} \\ \iff \frac{4}{x}=\frac{5}{6} \\ \iff x=\frac{4.6}{5}=\mathrm{4,8} \end{gathered}$$

Vì ΔADO vuông tại A nên áp dụng định lý Pytago ta có:

AD² + AO² = OD²

$\iff$4² + AO² = 5²

$\iff$ AO² = 5² - 4² = 9

=> AO = 3

Xét 2 tam giác vuông ΔCEO (CEO = 90⁰) và ΔCAB (CAB = 90⁰) có: C chung

$$\begin{gathered} \Rightarrow \frac{CO}{CB}=\frac{CE}{CA} \\ \iff \frac{CO}{CE+EB}=\frac{CE}{CO+OA} \\ \iff \frac{6}{\mathrm{4,8}+y}=\frac{\mathrm{4,8}}{6+3} \end{gathered}$$

$\Rightarrow$y = 6,45

Vậy x = 4,8; y = 6,45.

Bài 16: Cho ΔDHE ~ ΔABC với tỉ số đồng dạng $\frac{2}{3}$. Có bao nhiêu khẳng định đúng trong các khẳng định sau:

(I) Tỉ số hai đường cao tương ứng của ΔDHE và ΔABC là $\frac{2}{3}$.

(II) Tỉ số hai đường cao tương ứng của ΔABC và ΔDHE là $\frac{2}{3}$.

(III) Tỉ số diện tích của ΔABC và ΔDHE là $\frac{2}{3}$.

(IV) Tỉ số diện tích của ΔDHE và ΔABC là $\frac{4}{9}$.

A. 2

B. 1

C. 3

D. 4

Hiển thị đáp án  

Đáp án: A

Giải thích:

Vì ΔDHE ~ ΔABC với tỉ số đồng dạng  nên tỉ số hai đường cao tương ứng của ΔDHE và ΔABC là $\frac{2}{3}$  và tỉ số diện tích của ΔDHE và ΔABC là${\left(\frac{2}{3}\right)}^2 =\frac{4}{9}$

Do đó (I) và (IV) đúng, (II) và (III) sai.

Bài 17: Cho tam giác ABC cân tại A, đường cao CE. Tính AB, biết BC = 24cm và BE = 9cm.

B. 16cm

B. 32cm

C. 24cm

D. 18cm

Hiển thị đáp án  

Đáp án: B

Giải thích:

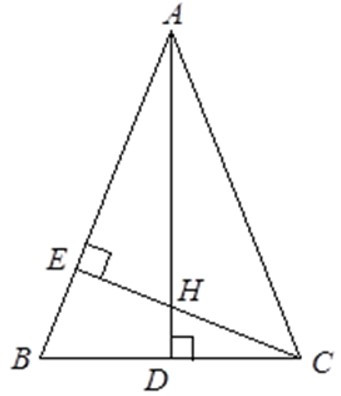
Kẻ đường cao AD.

Xét ΔCBE và ΔABD có

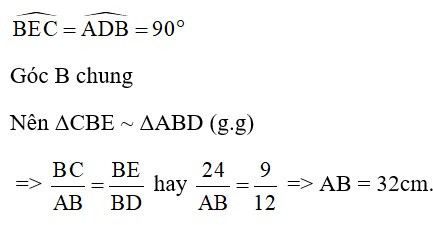
Bài 18: Cho tam giác ABC cân tại A, AC = 20cm, BC = 24cm, các đường cao AD và CE cắt nhau ở H. Tính độ dài HD.

B. 12cm

B. 6cm

C. 9cm

D. 10cm

Hiển thị đáp án  

Đáp án: C

Giải thích:

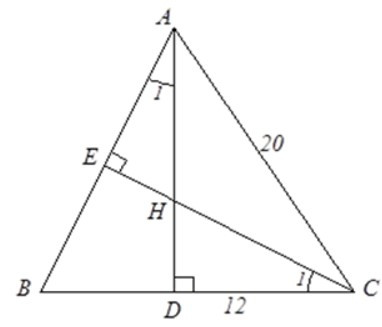
Tam giác ABC cân tại A  nên BD = DC

Suy ra HD = 9cm.

Bài 19: Cho tam giác vuông ABC vuông tại A, chân đường cao AH của tam giác ABC chia cạnh huyền BC thành hai đoạn thẳng BH = 4cm, HC = 9cm. Tính diện tích tam giác ABC?

A. S_ABC = 39cm²   

B. S_ABC = 36cm²

C. S_ABC = 78cm²   

D. S_ABC = 18cm²

Hiển thị đáp án  

Đáp án: A

Giải thích:

Áp dụng hệ thức lượng trong tam giác ABC vuông tại A

Ta có:

Vậy S_ABC = 1/2AB.AC = 1/2.2√(13) .3√(13) = 39( cm² )

Bài 20: Cho Δ ABC và Δ MNP có Aˆ = Mˆ = 90⁰, AB/MN = BC/NP thì?

A. Δ ABC ∼ Δ PMN

B. Δ ABC ∼ Δ NMP

C. Δ ABC ∼ Δ MNP

D. Δ ABC ∼ Δ MPN

Hiển thị đáp án  

Đáp án: C

Giải thích:

Ta có:

⇒ Δ ABC ∼ Δ MNP ( c - g - c )

Chọn đáp án C.

Bài 21: Nếu hai tam giác đồng dạng với nhau thì: Chọn phát biểu sai trong các phát biểu sau?

A. Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng.

B. Tỉ số hai đường phân giác tương ứng bằng tỉ số đồng dạng.

C. Tỉ số hai đường trung tuyến tương ứng bằng tỉ số đồng dạng.

D. Tỉ số các chu vi bằng 2 lần tỉ số đồng dạng.

Hiển thị đáp án  

Đáp án: D

Giải thích:

Áp dụng tính chất mở rộng

Nếu hai tam giác đồng dạng với nhau thì:

   + Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng.

   + Tỉ số hai đường phân giác tương ứng bằng tỉ số đồng dạng.

   + Tỉ số hai đường trung tuyến tương ứng bằng tỉ số đồng dạng.

   + Tỉ số các chu vi bằng tỉ số đồng dạng.

Đáp án D sai.

Bài 22: Cho hai tam giác ABC và DEF có Aˆ = Dˆ = 90⁰ ,AB = 3cm, BC = 5cm,EF = 10cm, DF = 6cm. Chọn phát biểu đúng trong các phát biểu sau?

A. Δ ABC ∼ Δ DEF   

B. Δ ABC ∼ Δ EDF

C. Δ ABC ∼ Δ DFE   

D. Δ ABC ∼ Δ FDE

Hiển thị đáp án  

Đáp án: C

Giải thích:

Ta có:

⇒ Δ ABC ∼ Δ DFE ( c - g - c )

Bài 23: Cho tam giác ABC có AB = 3cm; AC = 4cm và BC = 5cm. Tam giác MNP vuông tại M có MN = 6cm; MP = 8cm. Tìm khẳng định sai

A. Tam giác ABC là tam giác vuông

B. Δ ABC và ΔMNP đồng dạng với nhau

C. NP = 10 cm

D. Có hai phương án sai

Hiển thị đáp án  

Đáp án: D

Giải thích:

Ta có: AB² + AC² = BC² ( 3² + 4² = 5² = 25)

Suy ra: tam giác ABC vuông tại A

Xét Δ ABC và Δ MNP có:

Suy ra: Δ ABC và ΔMNP đồng dạng với nhau.

Áp dụng định lí Pyta go vào tam giác MNP có:

NP² = MN² + MP² = 6² + 8² = 100 nên NP = 10cm

Bài 24: Cho tam giác ABC vuông tại A, kẻ AH vuông góc BC. Tìm tam giác đồng dạng với tam giác ABC?

A. ΔHAC    

B. ΔAHC

C. ΔAHB    

D. ΔABH

Hiển thị đáp án  

Đáp án: A

Giải thích:

Xét ΔABC và ΔHAC có:

Suy ra: ΔABC đồng dạng với ΔHAC ( g.g)

Bài 25: Cho ta giác ABC vuông tại A, kẻ AH vuông góc BC. Biết BH = 25 và HC = 36. Tính AH?

A. 18cm    

B. 25cm

C. 20cm    

D. 32cm

Hiển thị đáp án  

Đáp án: C

Giải thích:

Xét ΔAHB và ΔCHA có:

Suy ra: ΔAHB và ΔCHA đồng dạng với nhau ( g.g)

Bài 26: Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC. Biết BC = 20cm, AC = 12cm. Tính BH?

A. 12cm    

B. 12,5cm

C. 15cm    

D. 12,8cm

Hiển thị đáp án  

Đáp án: D

Giải thích:

Áp dụng định lí Pytago vào tam giác ABC ta có:

BC² = AB² + AC² suy ra: AB² = BC² - AC² = 20² - 12² = 256

Nên AB = 16cm

* Xét tam giác AHB và tam giác CAB có:

Suy ra: Δ AHB và CAB đồng dạng ( g.g) .

Bài 27: Cho tam giác ABC vuông tại A, kẻ đường cao AH. Biết AH = 6cm, BH = 3cm. Tính AC?

Hiển thị đáp án  

Đáp án: C

Giải thích:

Bài 28: Cho tam giác ABC có AB = 3cm, AC = 4cm, BC = 5cm . Tam giác MNP đồng dạng với tam giác ABC và diện tích tam giác MNP là 96cm². Tính độ dài các cạnh của tam giác MNP?

A. 9cm, 12cm, 15cm

B. 12cm, 16cm ; 20cm

C. 6cm, 8cm, 10cm

D. Đáp án khác

Hiển thị đáp án  

Đáp án: A

Giải thích:

Ta có: AB² + AC² = BC² (3² + 4² = 5²)

Suy ra: tam giác ABC vuông tại A.

Diện tích tam giác ABC là:

*Gọi tam giác ABC đồng dạng với tam giác MNP theo tỉ số k

Suy ra:

Thay số

Các câu hỏi trắc nghiệm Toán lớp 8 có đáp án, chọn lọc khác:

Trắc nghiệm Khái niệm về hai tam giác đồng dạng có đáp án

Trắc nghiệm Trường hợp đồng dạng thứ nhất của tam giác có đáp án

Trắc nghiệm Trường hợp đồng dạng thứ hai của tam giác có đáp án

Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án

Trắc nghiệm Bài Ôn tập Chương 3 có đáp án