Nội dung bài viết

    Xem thêm

    TOP 40 câu Trắc nghiệm Những hằng đẳng thức đáng nhớ (tiếp theo p2) (có đáp án 2022) - Toán 8

    Bộ 40 câu hỏi trắc nghiệm Toán lớp 8 Bài 5: Những hằng đẳng thức đáng nhớ (tiếp theo p2) có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 8 Bài 5.

    1 2,007 24/06/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Trắc nghiệm Toán 8 Bài 5: Những hằng đẳng thức đáng nhớ (tiếp theo p2)

    Bài giảng Trắc nghiệm Toán 8 Bài 5: Những hằng đẳng thức đáng nhớ (tiếp theo p2)

    Bài 1: Chọn câu sai.

    A. A3 + B3 = (A + B)(A2 – AB + B2)            

    B. A3 - B3 = (A - B)(A2 + AB + B2)

    C. (A + B)3 = (B + A)3                                   

    D. (A – B)3 = (B – A)3

    Đáp án: D

    Giải thích:

    Ta có A3 + B3

    = (A + B)(A2 – AB + B2)

    và A3 - B3

    = (A - B)(A2 + AB + B2) nên A, B đúng.

    Vì A + B = B + A

    => (A + B)3 = (B + A)3 nên C đúng

    Vì A – B = - (B – A)

    => (A – B)3 = -(B – A)3 nên D sai

    Bài 2: Viết biểu thức

    (x – 3y)(x2 + 3xy + 9y2) dưới dạng hiệu hai lập phương

    A. x3 + (3y)3          

    B. x3 + (9y)3          

    C. x3 – (3y)3          

    D. x3 – (9y)3

    Đáp án: C

    Giải thích:

    Ta có (x – 3y)(x2 + 3xy + 9y2)

    = (x – 3y)(x + x.3y + (3y)2)

    = x3 – (3y)3

    Bài 3: Viết biểu thức

    (3x – 4)(9x2 + 12x + 16) dưới dạng hiệu hai lập phương

    A. (3x)3 – 163        

    B. 9x3 – 64            

    C. 3x3 – 43                  

    D. (3x)3 – 43

    Đáp án: D

    Giải thích:

    Ta có (3x – 4)(9x2 + 12x + 16)

    = (3x – 4)((3x)2 + 3x.4 + 42)

    = (3x)3 – 43

    Bài 4: Rút gọn biểu thức

    M = (2x + 3)(4x2 – 6x + 9) – 4(2x3 – 3)

    ta được giá trị của M là

    A. Một số lẻ                                         

    B. Một số chẵn     

    C. Một số chính phương                      

    D. Một số chia hết cho 5

    Đáp án: A

    Giải thích:

    Ta có

    M = (2x + 3)(4x2 – 6x + 9) – 4(2x3 – 3)

    = (2x + 3)[(2x)2 – 2x.3 + 32] – 8x3 + 12

    = (2x)3 + 33 – 8x3 + 12

    = 8x3 + 27 – 8x3 + 12 = 39

    Vậy giá trị của M là một số lẻ

    Bài 5: Giá trị của biểu thức

    E = (x + 1)(x2 – x + 1) – (x – 1)(x2 + x + 1) là

    A. 2                       

    B. 3                       

    C. 1                       

    D. 4

    Đáp án: A

    Giải thích:

    Ta có

    E = (x + 1)(x2 – x + 1) – (x – 1)(x2 + x + 1)

    = x3 + 1 – (x3 – 1)

    = x3 + 1 – x3 + 1 = 2

    Vậy E = 2

    Bài 6: Cho M = 8(x – 1)(x2 + x + 1) – (2x – 1)(4x2 + 2x + 1) và N = x(x + 2)(x – 2) – (x + 3)(x2 – 3x + 9) – 4x.

    Chọn câu đúng

    A. M = N              

    B. N = M + 2        

    C. M = N – 20      

    D. M = N + 20

    Đáp án: D

    Giải thích:

    Ta có

    M = 8(x – 1)(x2 + x + 1) – (2x – 1)(4x2 + 2x + 1)

    = 8(x3 – 1) – ((2x)3 – 1)

    = 8x3 – 8 – 8x3 + 1 = -7

    nên M = -7

    N = x(x + 2)(x – 2) – (x + 3)(x2 – 3x + 9) – 4x

    = x(x2 – 4) – (x3 + 33) + 4x

    = x3 – 4x – x3 – 27 + 4x

    = -27

    => N = -27

    Vậy M = N + 20

    Bài 7: Rút gọn biểu thức

    H = (x + 5)(x2 – 5x + 25) – (2x + 1)3 + 7(x – 1)3 – 3x(-11x + 5)

    ta được giá trị của H là

    A. Một số lẻ                                         

    B. Một số chẵn     

    C. Một số chính phương                      

    D. Một số chia hết cho 12

    Đáp án: A

    Giải thích:

    Ta có

    H = (x + 5)(x2 – 5x + 25) – (2x + 1)3 + 7(x – 1)3 – 3x(-11x + 5)

    = x3 + 53 – (8x3 + 3.(2x)2.1+ 3.2x.12 + 1) + 7(x3 – 3x2 + 3x – 1) + 33x2 – 15x

    = x3 + 125 – 8x3 – 12x2 – 6x – 1 + 7x3 – 21x2 + 21x – 7 + 33x2 – 15x

    = (x3 – 8x3 + 7x3) + (-12x2 – 21x2 + 33x2) + (-6x + 21x – 15x) + 125 – 1 – 7

    = 117

    Vậy giá trị của M là một số lẻ

    Bài 8: Giá trị của biểu thức

    A = (x2 – 3x + 9)(x + 3) – (54 + x3)

    A. 54                     

    B. -27                    

    C. -54                    

    D. 27

    Đáp án: B

    Giải thích:

    Ta có A = (x2 – 3x + 9)(x + 3) – (54 + x3)

    A = (x2 – 3x + 32)(x + 3) – (54 + x3)

    A = x3 + 33 – 54 – x3

    A = 27 – 54 = -27

    Vậy A = -27

    Bài 9: Viết biểu thức (x2 + 3)(x4 – 3x2 + 9)

    dưới dạng tổng hai lập phương

    A. (x2)3 + 33          

    B. (x2)3 – 33           

    C. (x2)3 + 93          

    D. (x2)3 – 93

    Đáp án: A

    Giải thích:

    Ta có (x2 + 3)(x4 – 3x2 + 9)

    = (x2 + 3)((x2)2 – 3.x2 + 32)

    = (x2)3 + 33

    Bài 10: Cho A = 13+ 23 + 33 + 43 + … + 103.

    Khi đó

    A. A chia hết cho 11                            

    B. A chia hết cho 5

    C. Cả A, B đều đúng                           

    D. Cả A, B đều sai

    Đáp án: C

    Giải thích:

    Ta có A = 13+ 23 + 33 + 43 + 53 + 63 + 73 + 83 + 93 + 103

    = (13 + 103) + (23 + 93) + (33 + 83) + (43 + 73) + (53 + 63)

    = 11(12 – 10 + 102) + 11(22 – 2.9 + 92) + … + 11(52 – 5.6 + 62)

    Vì mỗi số hạng trong tổng đều chia hết cho 11 nên A ⁝ 11.

    Lại có A = 13+ 23 + 33 + 43 + 53 + 63 + 73 + 83 + 93 + 103

    = (13 + 93) + (23 + 83) + (33 + 73) + (43 + 63) + (53 + 103)

    = 10(12 – 9 + 92) + 10(22 – 2.8 + 82) + … + 53 + 103

    Vì mỗi số hạng trong tổng đều chia hết cho 5 nên A ⁝ 5.

    Vậy A chia hết cho cả 5 và 11

    Bài 11: Cho a, b, c là các số thỏa mãn điều kiện

    a = b + c. Khi đó

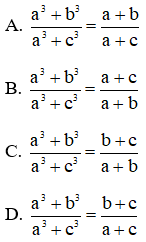
    Trắc nghiệm Những hằng đẳng thức đáng nhớ (tiếp theo p2) có đáp án - Toán lớp 8 (ảnh 1)

    Đáp án: A

    Giải thích:

    Ta có a3 + b3

    = (a + b)(a2 – ab + b2)

    mà a = b + c nên

    a3 + b3 = (a + b)(a2 – ab + b2)

    = (a + b)[(b + c)2 – (b + c)b + b2]

    = (a + b)(b2 + 2bc + c2 – b2 – bc + b2)

    = (a + b)(b2 + bc + c2)

    Tương tự ta có

    a3 + c3 = (a + c)(a2 – ac + c2)

    = (a + c)[(b + c)2 – (b + c)c + c2]

    = (a + c)(b2 + 2bc + c2 – c2 – bc + c2)

    = (a + c)(b2 + bc + c2)

    Bài 12: Cho (a + b + c)2 + 12 = 4(a + b + c) + 2(ab + bc + ca).

    Khi đó

    A. a = b = 2c         

    B. a = b = c           

    C. a = 2b = c         

    D. a = b = c = 2

    Đáp án: D

    Giải thích:

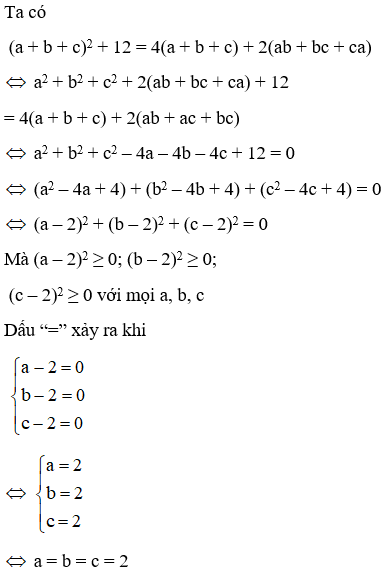
    Trắc nghiệm Những hằng đẳng thức đáng nhớ (tiếp theo p2) có đáp án - Toán lớp 8 (ảnh 1)

    Bài 13: Viết biểu thức(y2+6)(y24−3y+36)

    dưới dạng tổng hai lập phương

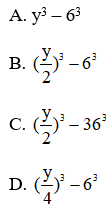
    Trắc nghiệm Những hằng đẳng thức đáng nhớ (tiếp theo p2) có đáp án - Toán lớp 8 (ảnh 1)

    Đáp án: B

    Giải thích:

    Ta có 

     (y2+6)(y24−3y+36) 

    =(y2+6)((y2)2−y2.6+62)

    =(y2)3−63

    Bài 14: Cho x thỏa mãn

    (x + 2)(x2 – 2x + 4) – x(x2 – 2) = 14. Chọn câu đúng.

    A. x = -3               

    B. x = 11               

    C. x = 3                 

    D. x = 4

    Đáp án: C

    Giải thích:

    Ta có

    (x + 2) (x2 – 2x + 4) – x(x2 – 2) = 14

    ⇔ x3 + 23 – (x3 – 2x) = 14

    ⇔ x3 + 8 – x3 + 2x = 14

    ⇔ 2x = 6

    ⇔ x = 3

    Vậy x = 3

    Bài 15: Điền vào chỗ trống: A=12x-y2=14x2-...+y2

    A. 2xy   

    B. xy 

    C. - 2xy   

    D. 12xy

    Đáp án: B

    Giải thích:

    Bài 16: Điều vào chỗ trống: ...=(2x-1)4x2+2x+1. 

    A. 1-8x3

    B. 1-4x3

    C.x3-8

    D. 8x3-1

    Đáp án: D

    Giải thích:

    Bài 17: Điền vào chỗ chấm : ( x - 2y )( x2 + 2xy + 4y2 ) =.......

    A. x3 - 8y3

    B. x3 - y3

    C. 8x3 - y3

    D. x3 + 8y3

    Đáp án: A

    Giải thích:

    ( x - 2y )( x2 + 2xy + 4y2 ) = ( x )3 - ( 2y )3 = x3 - 8y3.

    Bài 18: Viết biểu thức (3x – 4)(9x2 + 12x + 16) dưới dạng hiệu hai lập phương

     

    A. 3x3-163

    B. 9x3-64

    C. 3x3-43

    D. (3x)3-43

    Đáp án: D

    Giải thích:

    Ta có

    (3x – 4)(9x2 + 12x + 16) = (3x – 4)((3x)2 + 3x.4 + 42) = (3x)3 – 43

    Đáp án cần chọn là: D

    Bài 19: Tìm x biết x3 + 3x2 + 3x + 1 = 0

    A. x = -1

    B. x = 1

    C. x = -2

    D. x = 0

    Đáp án: A

    Giải thích:

    x3+3x2+3x+1=0x+13=0x+1=0x=-1

    Bài 20: Cho biểu thức A = x3 – 3x2 + 3x. Tính giá trị của A khi x = 1001

    A. 10003

    B. 10003-1

    C. 1000

    D. 10003+1

    Đáp án: D

    Giải thích:

    A = x3 – 3x2 + 3x = x3 – 3x2 + 3x – 1 + 1 = (x – 1)3 + 1

    Thay x = 1001 vào A = (x – 1)3 + 1 ta được

    A = (1001 – 1)3 + 1 suy ra A = 10003 + 1

    Bài 21: Cho biểu thức B = x3 – 6x2 + 12x + 10. Tính giá trị của B khi x = 1002

    A. 10003

    B. 10003+18

    C. 1000

    D. 10003-2

    Đáp án: B

    Giải thích:

    B = x3 – 6x2 + 12x + 10  = x3 – 3x2.2 + 3x.22 – 8 + 18 = (x – 2)3 + 18

    Thay x = 1002 vào B = (x – 2)3 + 18 ta được:

    B = (1002 – 2)3 + 18 = 10003 + 18

    Bài 22: Rút gọn biểu thứcM = (2x + 3)(4x2 – 6x + 9) – 4(2x3 – 3)ta được giá trị của M là

    A. Một số lẻ

    B. Một số chẵn

    C. Một số chính phương

    D. Một số chia hết cho 5

    Đáp án: A

    Giải thích:

    M = (2x + 3)(4x2 – 6x + 9) – 4(2x3 – 3)  = (2x + 3)[(2x)2 – 2x.3 + 32] – 8x3 + 12  = (2x)3 + 33 – 8x3 + 12 = 8x3+ 27 – 8x3 + 12 =39

    Vậy giá trị của M là một số lẻ.

    Bài 23: Giá trị của biểu thức P = -2(x3 + y3) + 3(x2 + y2) khi x + y = 1 là

    A. 3

    B. 1

    C. 5

    D. 0

    Đáp án: A

    Giải thích:

     x3 + y3= (x + y)3 – 3xy(x + y)

     x2 + y2 = (x + y)2 – 2xy

    Khi đó

    P = -2(x3 + y3) + 3(x2 + y2)  = -2[(x + y)3 – 3xy(x + y)] + 3[(x + y)2 – 2xy]

    Vì x + y = 1 nên ta có:

    P = -2(1 – 3xy) + 3(1 – 2xy) = -2 + 6xy + 3 – 6xy = 1

    Vậy P = 1.

    Đáp án cần chọn là: B

    Bài 24: Giá trị của biểu thức Q = a3 + b3  biết a + b = 5 và ab = -3.

    A. Q = 170   

    B. Q = 140

    C. Q = 80

    D. Q = -170

    Đáp án: A

    Giải thích:

    Ta có: (a + b)3 = a3 + 3a2b + 3ab2 + b3 = a3 + b3 + 3ab(a + b)

    Suy ra a3 + b3 = (a + b)3 – 3ab(a + b)

    Hay Q = (a + b)3 – 3ab(a + b)

    Thay a + b = 5 và a.b = -3 vào Q = (a + b)3 – 3ab(a + b) ta được

    Q = 53 – 3.(-3).5 = 170

    Vậy Q = 170.

    Các câu hỏi trắc nghiệm Toán lớp 8 có đáp án, chọn lọc khác:

    Trắc nghiệm Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung có đáp án

    Trắc nghiệm Phân tích đa thức thành nhân tử bằng phương pháp hằng đẳng thức có đáp án

    Trắc nghiệm Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử có đáp án

    Trắc nghiệm Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp có đáp án

    Trắc nghiệm Chia đơn thức cho đơn thức có đáp án

    Tham khảo các loạt bài Trắc nghiệm lớp 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 2,007 24/06/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: