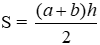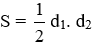TOP 40 câu Trắc nghiệm Hình thang (có đáp án 2023) - Toán 8
Bộ 40 câu hỏi trắc nghiệm Toán lớp 8 Bài 2: Hình thang có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 8 Bài 2.
Trắc nghiệm Toán 8 Bài 2: Hình thang
Bài giảng Trắc nghiệm Toán 8 Bài 2: Hình thang
Bài 1: Hãy chọn câu sai.
A. Hình thang là tứ giác có hai cạnh đối song song.
B. Nếu hình thanh có hai cạnh bên song song thì tất cả các cạnh của hình thang bằng nhau.
C. Nếu một hình thang có hai cạnh đáy bằng nhau thị hai cạnh bên bằng nhau, hai cạnh bên song song.
D. Hình thang vuông là hình thang có một góc vuông.
Đáp án: B
Giải thích:
+ Hình thang là tứ giác có hai cạnh đối song song nên A đúng.
+ Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau nên B sai vì cạnh bên và cạnh đáy chưa chắc bằng nhau.
+ Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau nên C đúng.
+ Hình thang vuông là hình thang có một góc vuông nên D đúng.
Bài 2: Hình thang ABCD có = 800; = 500, = 1000. Số đo góc là:
A. 1300
B. 1400
C. 700
D. 1200
Đáp án: A
Giải thích:
Vì tổng các góc của một tứ giác bằng 3600 nên = 3600
=> = 3600 – 800 – 500 – 1000 = 1300.
Bài 3: Góc kề cạnh bên của hình thang có số đo là 1300. Góc kề còn lại của cạnh bên đó là:
A. 700
B. 1000
C. 400
D. 500
Đáp án: D
Giải thích:
Vì tổng hai góc kề cạnh bên của hình thang bằng 1800 nên góc kề còn lại của cạnh bên đó có số đo bằng 1800 – 1300 = 500.
Bài 4: Cho hình thang vuông ABCD có = 900, AB = AD = 2cm, DC = 4cm. Tính góc ABC của hình thang.
A. 1370
B. 1360
C. 360
D. 1350
Đáp án: D
Giải thích:
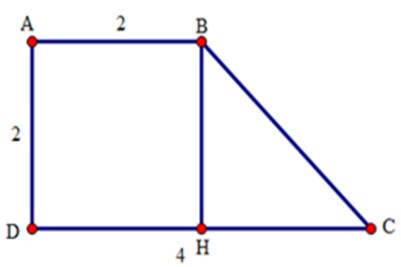
Từ B kẻ BH vuông góc với CD.
Tứ giác ABHD là hình thang có hai cạnh bên AD // BH nên AD = BH, AB = DH.
Mặt khác, AB = AD = 2cm nên suy ra BH = DH = 2cm.
Do đó: HC = DC – HD = 4 – 2 = 2cm.
Tam giác BHC có BH = HC = 2cm nên tam giác BHC cân đỉnh H.
Lại có = 900 (do BH ⊥ CD) nên tam giác BHC vuông cân tại H.
Do đó = (1800 - ) : 2
= (1800 – 900) : 2 = 450
Xét hình thang ABCD có:
= 3600 – ()
= 3600 – (900 + 900 + 450) = 1350.
Vậy = 1350.
Bài 5: Hình thang ABCD có = 700; = 650, = 1150. Số đo góc là:
A. 1300
B. 1400
C. 700
D. 1100
Đáp án: D
Giải thích:
Vì tổng các góc của một tứ giác bằng 3600 nên

Bài 6: Câu nào sau đây là đúng khi nói về hình thang:
A. Hình thang là tứ giác có hai cạnh đối song song.
B. Hình thang là tứ giác có hai cạnh đối bằng nhau
C. Hình thang là tứ giác có hai cạnh kề bằng nhau
D. Cả A, B, C đều sai
Đáp án: A
Giải thích:
Theo định nghĩa: ”Hình thang là tứ giác có hai cạnh đối song song” nên A đúng.
Bài 7: Góc kề cạnh bên của hình thang có số đo là 700. Góc kề còn lại của cạnh bên đó là:
A. 700
B. 1200
C. 1100
D. 1800
Đáp án: C
Giải thích:
Vì tổng hai góc kề cạnh bên của hình thang bằng 1800 nên góc kề còn lại của cạnh bên đó có số đo bằng 1800 – 700 = 1100.
Bài 8: Cho tứ giác ABCD có BC = CD và DB là tia phân giác của góc D. Chọn khẳng định đúng
A. ABCD là hình thang
B. ABCD là hình thang vuông
C. ABCD là hình thang cân
D. Cả A, B, C đều sai
Đáp án: A
Giải thích:
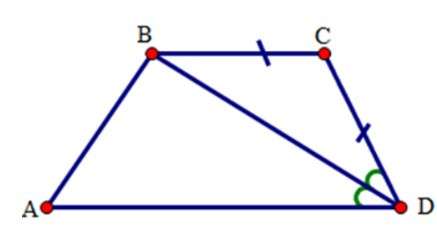
Xét ΔBCD có BC = CD (gt) nên ΔBCD là tam giác cân.

Bài 9: Cho hình thang ABCD có = 900, DC = BC = 2.AB, DC = 4cm. Tính góc ABC của hình thang.
A. 1100
B. 1500
C. 1200
D. 1350
Đáp án: C
Giải thích:
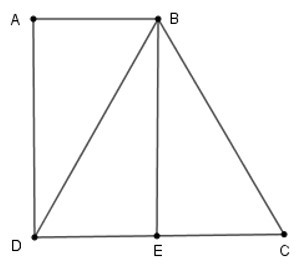
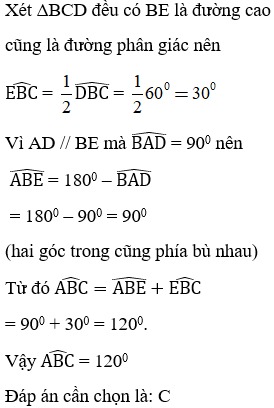
Bài 10: Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC, cắt các cạnh AB, AC lần lượt tại D và E.
1. Chọn khẳng định đúng nhất?
A. Tứ giác BDIC là hình thang
B. Tứ giác BIEC là hình thang
C. Tứ giác BDEC là hình thang
D. Cả A, B, C đều đúng
Đáp án: D
Giải thích:
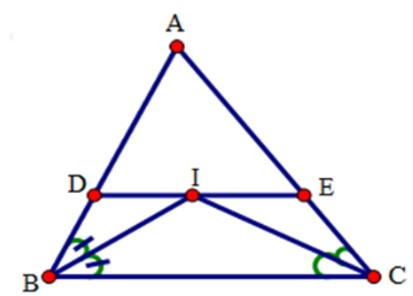
Xét tứ giác DECB có: DE // BC (gt) nên tứ giác DECB là hình thang.
Tương tự:
Tứ giác DICB có DI // BC (gt) nên tứ giác DICB là hình thang.
Tứ giác IECB có IE // CB (gt) nên tứ giác IECB là hình thang.
2. Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC, cắt các cạnh AB, AC lần lượt tại D và E.
Chọn khẳng định đúng.
A. DE > BD + CE
B. DE = BD + CE
C. DE < BD + CE
D. BC = BD + CE
Đáp án: B
Giải thích:
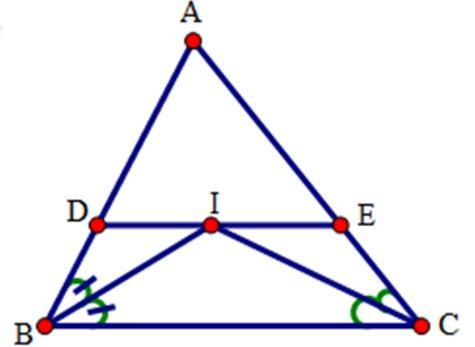

Bài 11: Cho tam giác ABC vuông tại A, đường cao AH. Trên BC lấy điểm M sao cho CM = CA. Đường thẳng đi qua M và song song với CA cắt AB tại I.
Chọn câu đúng nhất. Tứ giác ACMI là hình gì?
A. Hình thang cân
B. Hình thang vuông
C. Hình thang
D. Đáp án khác
Đáp án: C
Giải thích:
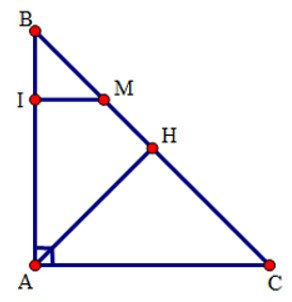
Tứ giác ACMI có: MI //AC (gt) và = 900 (gt) nên là hình thang vuông.
Bài 12: Chọn câu đúng trong các câu sau:
A. Hình thang có ba góc tù, một góc nhọn.
B. Hình thang có ba góc vuông, một góc nhọn.
C. Hình thang có ba góc nhọn, một góc tù.
D. Hình thanh có nhiều nhất hai góc nhọn và nhiều nhất hai góc tù.
Đáp án: C
Giải thích:
Ta có tổng các góc của hình thang bằng 3600.
+ Hình thang có ba góc tù, một góc nhọn.
Ví dụ: Hình thang có 3 góc tù là 1000,1200,1350 và 1 góc nhọn là 600.
⇒ Tổng 4 góc của hình thang bằng 1000 + 1200 + 1350 + 600 = 4150 > 3600
⇒ Không tồn tại hình thang có ba góc tù, một góc nhọn. ⇒ Đáp án A sai
+ Hình thang có ba góc vuông, một góc nhọn.
Ví dụ: Hình thang có 3 góc bằng 900 và một góc nhọn bằng 650.
⇒ Tổng 4 góc của hình thang bằng 900 + 900 + 900 + 650 = 3350 < 3600
⇒ Không tồn tại hình thang ba góc vuông, một góc nhọn. ⇒ Đáp án B sai.
+ Hình thang có ba góc nhọn, một góc tù.
Ví dụ: Hình thang có ba góc nhọn là 450,750,800, một góc tù là 1600
⇒ Tổng 4 góc của hình thang bằng 450 + 750 + 800 + 1600 = 3600
⇒ Tồn tại Hình thang có ba góc nhọn, một góc tù. ⇒ Đáp án C đúng
⇒ Hình thang có nhiều nhất là 3 góc nhọn. ⇒ Đáp án D sai.
Bài 13: Một hình thang có một cặp góc đối là 1250 và 750, cặp góc đối còn lại của hình thang đó là ?
A. 1050,550
B. 1050,450
C. 1150,550
D. 1150,650
Đáp án: A
Giải thích:
Tổng bốn góc của hình thang bằng 3600.
Theo giả thiết ta có một cặp góc đối là 1250 và 750
⇒ Tổng số đo góc của cặp góc đối còn lại là 1600.
Xét đáp án ta có cặp 1050,550 thỏa mãn.
Bài 14: Hình thang ABCD có Cˆ + Dˆ = 1500. Khi đó Aˆ + Bˆ = ?
A. 2200
B. 2100
C. 2000
D. 1900
Đáp án: B
Giải thích:
Tổng bốn góc của hình thang bằng 3600.
Khi đó ta có: Aˆ + Bˆ + Cˆ + Dˆ = 3600 ⇒ Aˆ + Bˆ = 3600 - ( Cˆ + Dˆ )
⇒ Aˆ + Bˆ = 3600 - 1500 = 2100.
Bài 15: Cho hình thang ABCD trong đó có Aˆ = 1200, Bˆ = 600, Dˆ = 1350 thì số đo của góc Cˆ = ?
A. 550
B. 450
C. 500
D. 600
Đáp án: B
Giải thích:
Tổng bốn góc của hình thang bằng 3600.
Khi đó ta có: Aˆ + Bˆ + Cˆ + Dˆ = 3600 ⇒ Cˆ = 3600 - ( Aˆ + Bˆ + Dˆ )
⇒ Cˆ = 3600 - ( 1200 + 600 + 1350 ) = 450.
Bài 16: Cho hình thang ABCD có AB // CD. Biết Aˆ = 100o, tính Dˆ
A. 80o
B. 100o
C. 120o
D. 50o
Đáp án: A
Giải thích:
Chọn đáp án A
Bài 17: Cho hình thang ABCD có AB // CD và Aˆ = 120o, Bˆ = 120o. Tính Cˆ, Dˆ
Đáp án: A
Giải thích:
Bài 18: Cho hình thang vuông ABCD vuông tại A và D. Biết AD = 3 cm và CD = 4cm. Tính AC?
A. 3cm
B. 4cm
C. 3,5cm
D. 5cm
Đáp án: D
Giải thích:
Do tứ giác ABCD là hình thang vuông nên Dˆ = 90o
Suy ra, tam giác ADC là tam giác vuông tại D.
Áp dụng đinh lí Py ta go vào tam giác vuông ACD ta có:
AC2 = AD2 + DC2 = 322 + 42 = 25
Suy ra: AC = 5cm
Bài 19: Cho tứ giác lồi ABCD có AB // CD và AD = 6cm; DC = 8cm và AC = 10cm. Tìm khẳng định sai ?
A. Tam giác ADC vuông tại D.
B. Tứ giác ABCD là hình thang
C. Tứ giác ABCD là hình thang vuông có Dˆ = 90o
D. Tứ giác ABCD là hình thang vuông có Bˆ = 90o
Đáp án: D
Giải thích:
Tứ giác ABCD có AB // CD nên tứ giác ABCD là hình thang có 2 đáy là AB và CD.
Xét tam giác ACD có: AD2 + CD2 = AC2 (62 + 82 = 102 = 100)
Suy ra: tam giác ADC là tam giác vuông tại D.
Do đó: Dˆ = 90o
Suy ra: Tứ giác ABCD là hình thang vuông có Dˆ = 90o
Vậy khẳng định D sai
Chọn đáp án D
Bài 20: Cho hình thang ABCD có AB // CD và Aˆ = 2Dˆ. Tính góc A?
A. 60o
B. 120o
C. 90o
D. 80o
Đáp án: B
Giải thích:
Chọn đáp án B
Bài 21: Cho hình thang ABCD có AB // CD và Cˆ - Bˆ = 30o . Tính góc C?
A. 105o
B. 90o
C. 75o
D. 60o
Đáp án: A
Giải thích:
Bài 22: Cho hình thang vuông ABCD vuông tại A và D. Biết AD = 6 cm và CD = 8cm. Tính AC?
A. 2cm
B. 14cm
C. 10cm
D. 5cm
Đáp án: D
Giải thích:
Do tứ giác ABCD là hình thang vuông nên Dˆ = 90o
Suy ra, tam giác ADC là tam giác vuông tại D.
Áp dụng đinh lí Py ta go vào tam giác vuông ACD ta có:
AC2 = AD2 + DC2 = 62 + 82 = 100
Suy ra: AC = 10cm
Chọn đáp án D
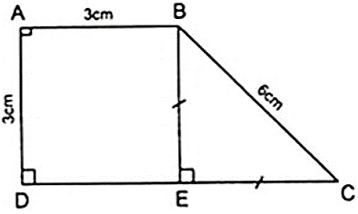
Bài 23: Hình thang vuông ABCD có góc A = góc D = 900; AB = AD = 3cm;CD = 6cm. Tính số đo góc B và C của hình thang ?
A. 1350.
B. 450.
C. 1200.
D. 1150.
Đáp án: A
Giải thích:
Kẻ BE ⊥ CD thì AD//BE do cùng vuông góc với CD
+ Hình thang ABED có cặp cạnh bên song song là hình bình hành.
Áp dụng tính chất của hình bình hành ta có
AD = BE = 3cm
Xét Δ BEC vuông tại E có
⇒ Δ BEC là tam giác vuông cân tại E.
Khi đó ta có: Cˆ = 450 và ABCˆ = 900 + 450 = 1350.
Bài 24: Góc kề cạnh bên của hình thang có số đo là 600. Góc kề còn lại của cạnh bên đó là:
A. 700
B. 1200
C. 1100
D. 1800
Đáp án: B
Giải thích:
Vì tổng hai góc kề cạnh bên của hình thang bằng 1800 nên góc kề còn lại của cạnh bên đó có số đo bằng 1800 – 600 = 1200.
Bài 25: Hình thang có:
A. hai cạnh đối song song.
B. hai cạnh đối bằng nhau
C. hai cạnh kề bằng nhau
D. Cả A, B, C đều sai
Đáp án: A
Giải thích:
Theo định nghĩa: ”Hình thang là tứ giác có hai cạnh đối song song” nên A đúng.
Bài 26: Hình thang có nhiều nhất bao nhiêu góc tù?
A. 0
B. 1
C. 2
D. 3
Đáp án: C
Giải thích:
Giải thích:
Xét hình thang ABCD có AB// CD
và là hai góc kề với cạnh bên.
(2 góc trong cùng phía ) nên trong hai góc đó có nhiều nhất 1 góc nhọn và có nhiều nhất là 1 góc tù.
và là hai góc kề với cạnh bên
(2 góc trong cùng phía) nên trong hai góc đó có nhiều nhất 1 góc nhọn và có nhiều nhất 1 góc tù. Vậy bốn góc là : có nhiều nhất là hai góc nhọn và nhiều nhất là hai góc tù.
Bài 27: Góc kề cạnh bên của hình thang có số đo là 1300. Góc kề còn lại của cạnh bên đó là:
A. 700
B. 500
C. 1300
D. 1800
Đáp án: A
Giải thích:
Vì tổng hai góc kề cạnh bên của hình thang bằng 1800 nên góc kề còn lại của cạnh bên đó có số đo bằng 1800 – 1300 = 500.
Bài 25: Có bao nhiêu hình thang trong hình:
A. 8
B. 9
C. 10
D. 12
Đáp án: C
Giải thích:
Trên hình vẽ có tất cả 10 hình thang.
Đó là: ABCD, ABEF, ABGH, ABIK, DCEF, DCGH, DCIK, FEGH, FEIK, HGIK
Bài 28: Các góc của một tứ giác lập thành cấp số cộng. Nếu góc nhỏ nhất là 750 , thì góc lớn nhất là:
A. 900
B. 950
C. 1050
D. 1000
Đáp án: A
Giải thích:
Các góc liên tiếp của một hình thang lập thành một cấp số cộng.Nếu góc nhỏ nhất là 750 thì góc lớn nhất
là: 105 độ
Bài 29: Hình thang có một cặp góc đối là 125 độ và 65 độ tìm cặp góc đối còn lại
A. 1200 và 600
B. 1150 và 550
C. 1000 và 800
D. 1050 và 750
Đáp án: D
Bài 30: Hình thang vuông là:
A. hình thang có một góc vuông.
B. tứ giác có một góc vuông
C. tứ giác có hai cạnh đối song song
D. Cả A, B, C đều sai
Đáp án: A
Giải thích: Hình thang có một góc vuông là hình thang vuông.
Bài 31: Nếu một hình thang có hai cạnh bên ...... thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau.
A. bằng nhau
B. song song
C. vuông góc
D. Cắt nhau
Đáp án: B
Giải thích:
Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau.
Bài 32: Có bao nhiêu hình thang trong hình:
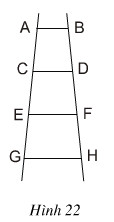
A. 8
B. 6
C. 10
D. 4
Đáp án: C
Giải thích:
Có tất cả 6 hình thang, đó là: ABDC, CDFE, EFHG, ABFE, CDHG, ABHG
Bài 33: Góc kề cạnh bên của hình thang có số đo là 1000. Góc kề còn lại của cạnh bên đó là:
A. 700
B. 800
C. 1000
D. 1800
Đáp án: A
Giải thích:
Vì tổng hai góc kề cạnh bên của hình thang bằng 1800 nên góc kề còn lại của cạnh bên đó có số đo bằng 1800 – 1000 = 800.
Bài 34: Cho hình thang vuông ABCD vuông tại A và D. Biết AD = 3 cm và AC= 5cm. Tính DC?
A. 2cm
B. 4cm
C. 5cm
D. 8cm
Đáp án: B
Giải thích:
Do tứ giác ABCD là hình thang vuông nên Dˆ = 90o
Suy ra, tam giác ADC là tam giác vuông tại D.
Áp dụng đinh lí Py ta go vào tam giác vuông ACD ta có:
DC2 = AC2- AD2 = 52 - 32 = 16
Suy ra: DC = 4cm
Bài 35: Có bao nhiêu hình thang trong hình:
.png)
A. 1
B. 2
C. 3
D. 4
Đáp án: B
Giải thích:
Do tứ giác ABCD là hình thang vuông nên Dˆ = 90o
Suy ra, tam giác ADC là tam giác vuông tại D.
Áp dụng đinh lí Py ta go vào tam giác vuông ACD ta có:
DC2 = AC2- AD2 = 52 - 32 = 16
Suy ra: DC = 4cm
Bài 36: Cho hình thang vuông ABCD vuông tại A và D. Biết AC = 10 cm và CD = 8cm. Tính AD?
A. 2cm
B. 18cm
C. 9cm
D. 6cm
Đáp án: D
Giải thích:
Do tứ giác ABCD là hình thang vuông nên Dˆ = 90o
Suy ra, tam giác ADC là tam giác vuông tại D.
Áp dụng đinh lí Py ta go vào tam giác vuông ACD ta có:
AD2 = AC2- DC2 = 102 - 82 = 36
Suy ra: AD = 6cm
Bài 37: Có bao nhiêu hình thang vuông trong hình:
A. 5
B. 7
C. 8
D. 4
Đáp án: C
Giải thích:
Các hình thang vuông:
AMND; MBCN; ABKI; KCD, AMND, BMNC, CKID, AIKB
Bài 38: Cho tứ giác lồi ABCD có AB // CD và AD = 3cm; DC = 4cm và AC = 5cm. Tìm khẳng định sai ?
A. Tứ giác ABCD là hình thang
B. Tam giác ADC vuông tại D.
C. Tứ giác ABCD là hình thang vuông có Dˆ = 90o
D. Tứ giác ABCD là hình thang vuông có Bˆ = 90o
Đáp án: D
Giải thích:
Tứ giác ABCD có AB // CD nên tứ giác ABCD là hình thang có 2 đáy là AB và CD.
Xét tam giác ACD có: AD2 + CD2 = AC2 (32 + 42 = 52 = 25)
Suy ra: tam giác ADC là tam giác vuông tại D.
Do đó: Dˆ = 90o
Suy ra: Tứ giác ABCD là hình thang vuông có Dˆ = 90o
Bài 39: Chọn câu sai:
A. Diện tích hình thang bằng nửa tích của tổng hai đáy với chiều cao
B. Diện tích hình hình hành bằng tích của một cạnh với chiều cao tương ứng với cạnh đó.
C. Diện tích hình bình hành bằng nửa tích của một cạnh với chiều cao tương ứng với cạnh đó
D. Diện tích hình thoi bằng nửa tích hai đường chéo
Đáp án: C
Giải thích:
+ Diện tích hình thang bằng nửa tích của tổng hai đáy với chiều cao:
+ Diện tích hình bình hành bằng tích một cạnh với chiều cao ứng với cạnh đó: S = a. h
+ Diện tích hình thoi bằng nửa tích hai đường chéo:
Bài 40: Chọn ý đúng
A. Trong một hình thang, hai góc kề một cạnh bên thì phụ nhau
B. Trong một hình thang, hai góc kề một cạnh bên thì bù nhau
C. Trong một hình thang, hai góc kề một đáy thì bù nhau
D. Trong một hình thang, hai góc kề một đáy thì phụ nhau
Đáp án: B
Các câu hỏi trắc nghiệm Toán lớp 8 có đáp án, chọn lọc khác:
Trắc nghiệm Hình thang cân có đáp án
Trắc nghiệm Đường trung bình của tam giác, của hình thang có đáp án
Trắc nghiệm Đối xứng trục có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Sinh học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Toán lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Hóa học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn lớp 11 có đáp án
- Trắc nghiệm Tiếng Anh lớp 11 có đáp án
- Trắc nghiệm Vật Lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Địa lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm GDCD lớp 11 có đáp án
- Trắc nghiệm Lịch sử lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Công nghệ lớp 11 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 11 có đáp án
- Trắc nghiệm Tin học lớp 11 có đáp án
- Trắc nghiệm Toán lớp 12 có đáp án
- Trắc nghiệm Sinh học lớp 12 có đáp án
- Trắc nghiệm Hóa học lớp 12 có đáp án
- Trắc nghiệm Ngữ văn lớp 12 có đáp án
- Trắc nghiệm Tiếng Anh lớp 12 có đáp án
- Trắc nghiệm Địa lí lớp 12 có đáp án
- Trắc nghiệm Vật Lí lớp 12 có đáp án
- Trắc nghiệm Công nghệ lớp 12 có đáp án
- Trắc nghiệm Giáo dục công dân lớp 12 có đáp án
- Trắc nghiệm Lịch sử lớp 12 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 12 có đáp án




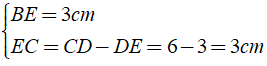
.PNG)