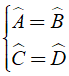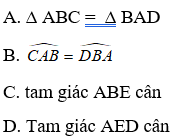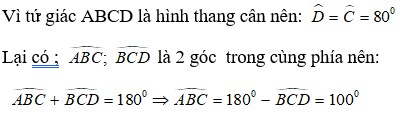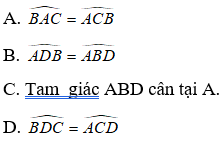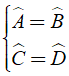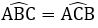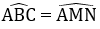TOP 40 câu Trắc nghiệm Hình thang cân (có đáp án 2023) - Toán 8
Bộ 40 câu hỏi trắc nghiệm Toán lớp 8 Bài 3: Hình thang cân có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 8 Bài 3.
Trắc nghiệm Toán 8 Bài 3: Hình thang cân
Bài giảng Trắc nghiệm Toán 8 Bài 3: Hình thang cân
Bài 1: Chọn câu đúng nhất.
A. Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
B. Trong hình thang cân, hai cạnh bên bằng nhau.
C. Trong hình thang cân, hai đường chéo bằng nhau
D. Cả A, B, C đều đúng
Đáp án: D
Giải thích:
+ Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
+ Trong hình thang cân, hai cạnh bên bằng nhau.
+ Trong hình thang cân, hai đường chéo bằng nhau.
Vậy cả A, B, C đều đúng
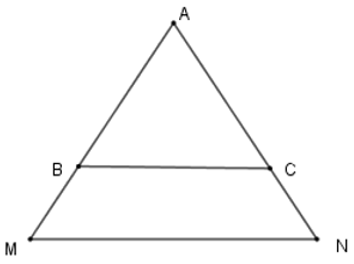
Bài 2: Cho tam giác ΔAMN cân tại A. Các điểm B, C lần lượt trên các cạnh AM, AN sao cho AB = AC. Hãy chọn câu đúng:
A. MB = NC
B. BCNM là hình thang cân
C.
D. Cả A, B, C đều đúng
Đáp án: D
Giải thích:
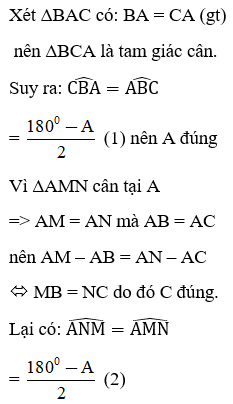

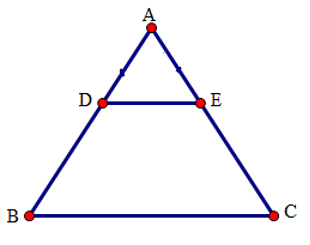
Bài 3: Cho tam giác ABC cân tại A. Gọi D, E theo thứ tự thuộc các cạnh bên AB, AC sao cho AD = AE.
Tứ giác BDEC là hình gì?
A. Hình thang
B. Hình thang vuông
C. Hình thang cân
D. Cả A, B, C đều sai
Đáp án: C
Giải thích:


Bài 4: Cho tam giác ABC cân tại A. Gọi D, E theo thứ tự thuộc các cạnh bên AB, AC sao cho DE // BC.
Chọn đáp án đúng nhất. Tứ giác BDEC là hình gì?
A. Hình thang
B. Hình thang vuông
C. Hình thang cân
D. Cả A, B, C đều sai
Đáp án: C
Giải thích:
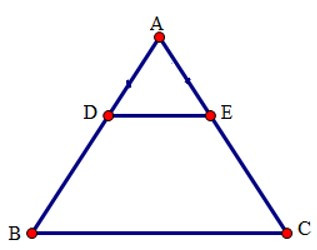
Tứ giác BDEC có DE // BC nên tứ giác BDEC là hình thang.
Lại có (vì tam giác ABC cân tại A) nên BDEC là hình thang cân
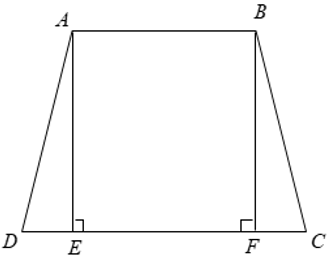
Bài 5: Cho hình thang cân MNPQ (MN // PQ) có góc = 450 và hai đáy có độ dài 12cm, 40cm. Diện tích của hình thang cân là:
A. 728 cm2
B. 346 cm2
C. 364 cm2
D. 362 cm2
Đáp án: C
Giải thích:
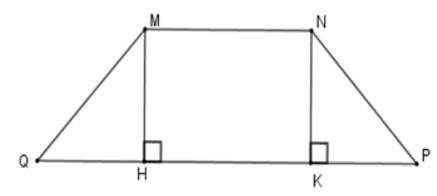
Kẻ MH ⊥ QP; NK ⊥ QP tại H, K => MH // NK
Tứ giác MNHK có MN // HK nên MNHK là hình thang, lại có MH // NK
=> MN = HK; MH = NK
(Vì hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau)
Lại có
MQ = NP (vì MNPQ là hình thang cân) suy ra ΔMQH = ΔNKP (ch – cgv)
=> QH = KP =
Mà HK = MN = 12 cm nên QH = KP = = 14 cm
Mà = 450 => ΔMHQ vuông cân tại H => MH = QH = 14 cm
Diện tích hình thang cân MNPQ là
SMNPQ = = 364 cm2
Đáp án cần chọn là: C
Bài 6: Cho hình thang cân MNPQ (MN // PQ) có góc = 450 và hai đáy có độ dài 8cm, 30cm. Diện tích của hình thang cân là:
A. 418 cm2
B. 209 cm2
C. 290 cm2
D. 580 cm2
Đáp án: B
Giải thích:
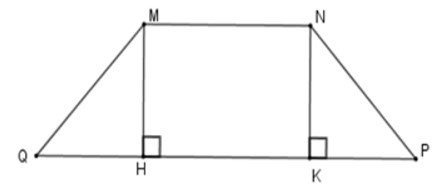
Kẻ MH ⊥ QP; NK ⊥ QP tại H, K => MH // NK
Tứ giác MNHK có MN // HK nên MNHK là hình thang, lại có MH // NK
=> MN = HK; MH = NK
(Vì hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau)
Lại có
MQ = NP (vì MNPQ là hình thang cân) suy ra ΔMQH = ΔNKP (ch – cgv)
=> QH = KP =
Mà HK = MN = 8 cm nên QH = KP = = 8 cm
Mà = 450 => ΔMHQ vuông cân tại H => MH = QH = 14 cm
Diện tích hình thang cân MNPQ là
SMNPQ = = 209 cm2
Bài 7: Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN. Tứ giác BMNC là hình gì?
A. Hình thang
B. Hình thang cân
C. Hình thang vuông
D. Cả A, B, C đều sai
Đáp án: B
Giải thích:
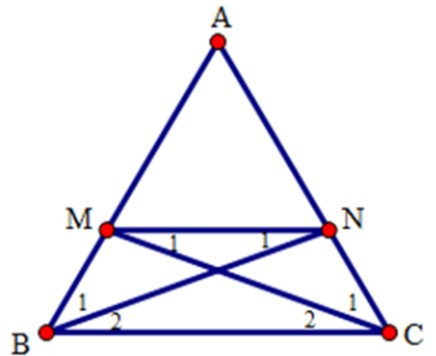


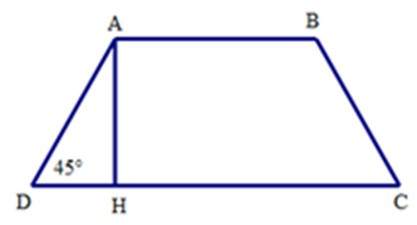
Bài 8: Cho hình thang cân ABCD có đáy nhỏ AB = 4cm, đường AH = 6cm, và = 450. Độ dài đáy lớn CD bằng
A. 12cm
B. 16 cm
C. 18 cm
D. 20 cm
Đáp án: B
Giải thích:

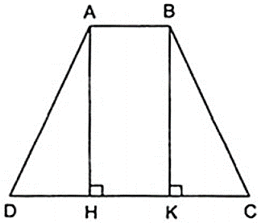
Bài 9: Cho hình thang cân ABCD đáy nhỏ AB = 12cm, đáy lớn CD = 22cm, cạnh bên BC = 13cm thì đường cao AH bằng:
A. 9 cm
B. 8 cm
C. 12 cm
D. 6 cm
Đáp án: C
Giải thích:
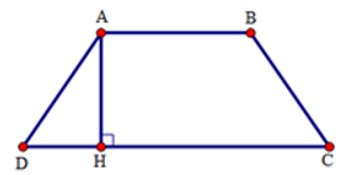
Ta có DH = (CD – AB)
= (22 – 12)
Do ABCD là hình thang cân nên AD = BC = 13 cm
Áp dụng định lí Py-ta-go vào tam giác ADH vuông tại H ta có
AD2 = AH2 + DH2
=> AH2 = AD2 – DH2 = 132 – 52
=> AH = 12
Vậy AH = 12cm
Bài 10: Cho hình thang cân ABCD có đáy nhỏ AB = 3cm, đường AH = 5cm, và = 450. Độ dài đáy lớn CD bằng
A. 13 cm
B. 10 cm
C. 12 cm
D. 8 cm
Đáp án: A
Giải thích:
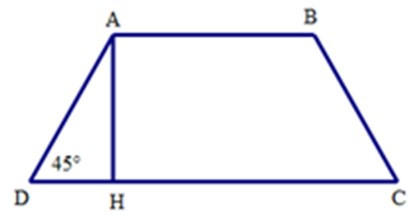
Ta có tam giác ADH vuông cân tại H vì = 450.
Do đó DH = AH = 5cm
Mà DH = (CD – AB)
Suy ra CD = 2DH + AB
= 2.5 + 3 = 13 (cm)
Vậy CD = 13 cm
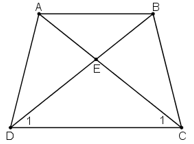
Bài 11: Cho hình thang cân ABCD (AB // CD) có hai đường chéo cắt nhau tại I, hai đường thẳng AD và BC cắt nhau ở K. Chọn câu sai.
A. ΔKAB cân tại K
B. ΔKCD cân tại K
C. ΔICD đều
D. KI là đường phân giác
Đáp án: C
Giải thích:
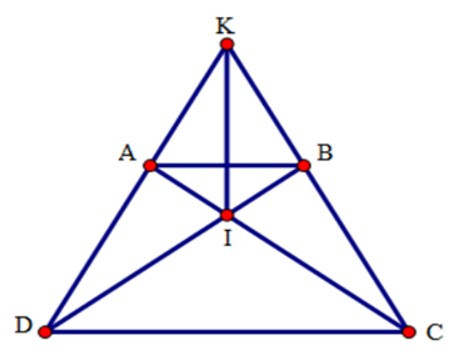
Xét tam giác ACD và tam giác BDC có:
+ AD = BC (do ABCD là hình thang cân)
+ AC = BD (do ABCD là hình thang cân)
+ CD là cạnh chung
Suy ra ΔACD = ΔBDC (c.c.c)
Suy ra (hai góc tương ứng), suy ra tam giác ICD cân tại I.
Nên C sai vì ta chưa đủ điều kiện để IC = CD
Tam giác KCD có hai góc ở đáy bằng nhau nên tam giác KCD cân ở K nên B đúng.
Xét tam giác KDI và tam giác KCI có:
+ KD = KC (do ΔKCD cân tại K))
+ KI là cạnh chung
+ IC = ID
Suy ra ΔKDI = ΔKCI (c.c.c)
Suy ra , do đó KI là phân giác nên D đúng.
Ta có AB // CD (do ABCD là hình thang) nên ; (các cặp góc đồng vị bằng nhau)
Mà (tính chất hình thang cân) nên (tính chất hình thang cân) nên hay ΔKAB cân tại K. Do đó A đúng
Bài 12: Cho hình thang cân ABCD (AB // CD) có hai đường chéo cắt nhau tại I, hai đường thẳng AD và BC cắt nhau ở K. Chọn khẳng định đúng:
A. KI là đường trung trực của hai đáy AB và CD
B. KI là đường trung trực của đáy AB nhưng không là đường trung trực của CD
C. KI là đường trung trực của đáy CD nhưng không là trung trực của AB
D. KI không là đường trung trực của cả hai đáy AB và CD.
Đáp án: A
Giải thích:
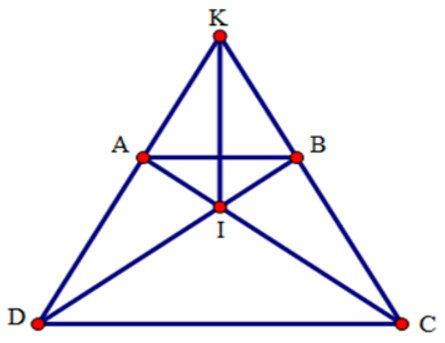
Xét tam giác ACD và tam giác BDC có:
+ AD = BC (do ABCD là hình thang cân)
+ AC = BD (do ABCD là hình thang cân)
+ CD là cạnh chung
Suy ra ΔACD = ΔBDC (c.c.c)
Suy ra (cmt), suy ra tam giác ICD cân tại I. Do đó ID = IC (1)
Tam giác KCD có hai góc ở đáy bằng nhau nên tam giác KCD cân ở K.
Do đó KC = KD (2)
Từ (1) và (2) suy ra KI là đường trung trực của CD (*).
Xét tam giác ADB và tam giác BCA có:
+ AD = BC (cmt)
+ AB là cạnh chung
+ AC = BD
Suy ra ΔADB = ΔBCA (c.c.c)
Suy ra
Xét tam giác IAB có nên tam giác IAB cân tại I.
Do đó IA = IB (3)
Ta có KA = KD – AD;
KB = KC – BC
Mà KD = KC, AD = BC,
do đó KA = KB (4)
Từ (3) và (4) suy ra KI là đường trung trực của AB. (**)
Từ (*) và (**) suy ra KI là đường trung trực của hai đáy (đpcm)
Bài 13: Cho hình thang cân ABCD (AB // CD). Giả sử AB ≤ CD, chọn câu đúng.
A. BD2 – BC2 = CD.AB
B. BD2 – BC2 = AB2
C. BD2 – BC2 = 2CD.AB
D. BD2 – BC2 = BC.AB
Đáp án: A
Giải thích:
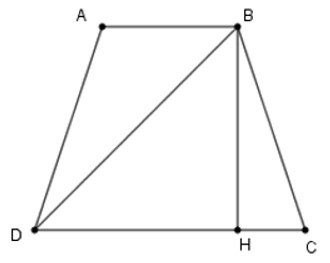
Kẻ BH ⊥ CD tại H.
Xét tam giác vuông BDH, theo định lý Pytago, ta có BD2 = DH2 + BH2
Xét tam giác vuông CBH, theo định lý Pytago, ta có BC2 = CH2 + BH2
Suy ra
BD2 – BC2 = (DH2 + BH2) – (CH2 + BH2)
= DH2 – CH2 = (BH + DH)(DH – BH)
= CD.AB
Bài 14: Cho hình thang cân ABCD đáy nhỏ AB = 4cm, đáy lớn CD = 10cm, cạnh bên BC = 5cm thì đường cao AH bằng:
A. 4,5 cm
B. 4 cm
C. 3,5 cm
D. 3 cm
Đáp án: B
Giải thích:
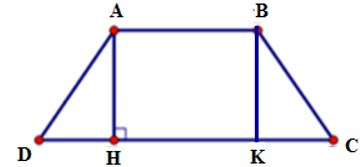
Kẻ BK ⊥ DC tại K.
Vì ABCD là hình thang cân nên ta có ; AD = BC
=> ΔAHD = ΔBKC (ch – gn) => DH = CK
Suy ra DH = (CD – AB)
Suy ra DH = (CD – AB) = (10 – 4)
Do ABCD là hình thang cân nên AD = BC = 5 cm
Áp dụng định lí Py-ta-go vào tam giác ADH vuông tại H ta có
AD2 = AH2 + DH2
=> AH2 = AD2 – DH2 = 52 – 32
=> AH = 4
Vậy AH = 4cm
Bài 15: Cho hình thang cân ABCD (AB // CD, AB < CD ). Kẻ các đường cao AE, BF của hình thang. So sánh DE và CF.
A. DE > CF
B. DE < CF
C. DE = CF
D. Không so sánh được
Đáp án: C
Giải thích:
Ta có ABCD là hình thang cân nên AD = BC
+ Xét tam giác vuông ADE có
AD2 = AE2 + DE2 ⇒ DE2 = AD2 - AE2 ⇔ DE = √( AD2 - AE2 ) ( 1 )
+ Xét tam giác vuông BCF có:
BC2 = BF2 + CF2 ⇒ CF2 = BC2 - BF2 ⇔ CF = √( BC2 - BF2 ) ( 2 )
Xét tứ giác ABFE có AB// EF nên là hình thang. Lại có hai cạnh bên AE// BF (cùng vuông góc CD ) nên AE = BF (3)
Từ ( 1 ), ( 2 ) và ( 3 ) ⇒ DE = CF (do AD = BC và AE = BF )
Bài 16: Cho hình thang cân ABCD( AB//CD,AB < CD ). Kẻ đường cao AH,BK của hình thang. Chứng minh rằng DH = CK.
A. DH < CK
B. DH > CK
C. DH = CK
D. Không so sánh được
Đáp án: C
Giải thích:
Áp dụng định nghĩa, tính chất và giả thiết của hình thang cân ta có: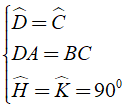
(trường hợp cạnh huyền – góc nhọn)
⇒ DH = CK (cặp cạnh tương ứng bằng nhau)
Vậy DH = CK. (đpcm)
Bài 17: Điền cụm từ thích hợp vào chỗ trống
A. Hình thang cân là…………………………………..
B. Hình thang có………………. là hình thang cân .
C. Hai cạnh bên của hình thang cân…………………..
D. Hình thang cân có hai góc kề một đáy…………….
Đáp án: A
Giải thích:
+ Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
→ Đáp án A điền: “hình thang có hai góc kề một đáy bằng nhau”.
+ Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
→ Đáp án B điền: “hai góc kề một đáy bằng nhau”
+ Hai cạnh bên của hình thang cân bằng nhau.
→ Đáp án C điền: “bằng nhau”
+ Hình thang cân là hình thang có hai góc kề một đáy bằng nhau
→ Đáp án D điền: “bằng nhau”
Bài 18: Điền chữ “Đ” hoặc “S” vào mỗi câu khẳng định sau:
A. Tứ giác có hai cạnh bên bằng nhau là hình thang cân.
B. Hình thang cân có hai cạnh bên bằng nhau.
C. Hình thang cân có hai góc kề một cạnh đáy bù nhau.
D. Hình thang cân có hai góc kề một cạnh đáy bằng nhau.
Đáp án: A
Giải thích:
+ Tứ giác có hai cạnh bên bằng nhau là hình thang cân.
→ Đáp án A sai vì hai cạnh bên bằng nhau chưa chắc tạo ra hình thang.
+ Hình thang cân có hai cạnh bên bằng nhau.
→ Đáp án B đúng.
+ Hình thang cân có hai góc kề một cạnh đáy bằng nhau.
→ Đáp án D đúng, đáp án C sai.
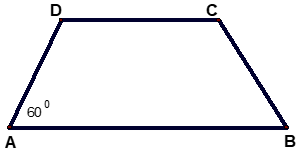
Bài 19: Cho hình thang cân ABCD (như hình vẽ) có BADˆ = 600. Số đo của BCDˆ = ?
A. 500
B. 600
C. 1200
D. 800
Đáp án: C
Giải thích:
Áp dụng tính chất của hình thang cân ta có:
Mà Aˆ + Bˆ + Cˆ + Dˆ = 3600 ⇔ 2Aˆ + 2Cˆ = 3600
⇒ 2Cˆ = 3600 - 2Aˆ = 3600 - 2.600 = 2400 ⇔ Cˆ = 1200
Chọn đáp án C.
Bài 20: Cho hình thang cân ABCD (AB // CD) . Tìm mệnh đề sai?
Đáp án: D
Giải thích:
Bài 21: Cho hình thang cân ABCD (AB// CD) và Dˆ = 80o. Tính ABCˆ
A. 100o
B. 90o
C. 80o
D. 110o
Đáp án: A
Giải thích:
Bài 22: Cho hình thang ABCD có AB // CD , hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD . Tìm khẳng định sai trong các khẳng định sau?
A. ABCD là hình thang cân
B. AC = BD
C. BC = AD
D. Tam giác AOD cân tại O.
Đáp án: D
Giải thích:
* Ta có: OA = OB nên tam giác OAB cân tại O
* Do OC = OD nên tam giác OCD cân tại O
* vì OA = OB và OC = OD nên OA + OC = OB + OD
Hay AC = BD
Hình thang ABCD có hai đường chéo AC = BD nên đây là hình thang cân.
Suy ra: BC = AD và BADˆ = ABCˆ; ADCˆ = DCB
Bài 23: Cho hình thang cân ABCD có AB // CD và Aˆ = 125o. Tính Bˆ ?
A. 125o
B. 65o
C. 90o
D. 55o
Đáp án: A
Giải thích:
Theo định nghĩa hình thang cân ta có: Aˆ = Bˆ = 125o
Bài 24: Cho hình thang cân ABCD có AB// CD và AB = BC. Tìm khẳng định sai.
Đáp án: D
Giải thích:
* Xét tam giác ABC có AB = BC nên tam giác ABC cân tại B.
Suy ra: BACˆ = ACBˆ
* Vì ABCD là hình thang cân nên AD = BC
Lại có AB = BC nên AB = AD.
* Suy ra: ΔABD cân tại A nên ADBˆ = ABDˆ
Bài 25: Cho hình thang cân ABCD có AB // CD. Gọi giao điểm của AD và BC là M . Tam giác MCD là tam giác gì ?
A. Tam giác cân
B. Tam giác nhọn
C. Tam giác vuông
D. Tam giác tù
Đáp án: A
Giải thích:
Vì ABCD là hình thang cân nên: Dˆ = Cˆ
Xét tam giác MCD có Dˆ = Cˆ nên đây là tam giác cân tại M
Bài 26:Hình thang cân ABCD (AB // CD) có , DB là tia phân giác của góc D. Tính cạnh CD của hình thang, biết chu vi hình thang bằng 20cm.
A. 20cm
B. 12cm
C. 8cm
D. 4cm
Đáp án: C
Giải thích:
Hình thang ABCD cân có AB // CD
⇒ = 60o
DB là tia phân giác của góc D
⇒
(hai góc so le trong)
Suy ra:
⇒ Δ ABD cân tại A ⇒ AB = AD (1)
Từ B kẻ đường thẳng song song với AD cắt CD tại E.
Hình thang ABED có hai cạnh bên song song nên AB = ED, AD = BE (2)
Mà (đồng vị )
Suy ra: = 60o
⇒ Δ BEC đều ⇒ EC = BC (3)
Ta có: AD = BC (tính chất hình thang cân) (4)
Từ (1), (2), (3) và (4) ⇒ AB = BC = AD = ED = EC
⇒ Chu vi hình thang bằng:
AB + BC + CD + AD = AB + BC + EC + ED + AD = 5AB
⇒AB = BC = AD = 20 : 5 = 4 (cm)
Suy ra CD = CE + DE = 2 AB = 2.4 = 8 (cm).
Bài 27: Hình thang cân ABCD (AB// CD) có = 70o. Khẳng định nào dưới đây là đúng ?
A. = 110o
B. = 110o
C. = 70o
D. = 70o
Đáp án: A
Giải thích:
Ta có: = 180° (hai góc trong cùng phía)
Suy ra: = 180° - = 180° - 70° =110°
Mà (tính chất hình thang cân)
Nên = 110°
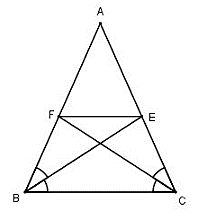
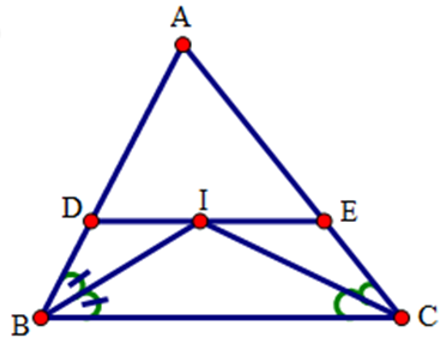
Bài 28: Cho tam giác ABC cân tại A, các đường phân giác BE, CF. So sánh BF, EF.
A. BF= EF
B. BF< EF
C. BF> EF
D. Không so sánh được
Đáp án: A
Giải thích:
+) Do BE và CF lần lượt là tia phân giác của góc B và góc C nên ta có:
Mà tam giác ABC cân tại A nên
Suy ra:
Xét hai tam giác AEB và AFC
Có AB = AC (ΔABC cân tại A)
(chứng minh trên)
là góc chung
⇒ ΔAEB = ΔAFC (g.c.g)
⇒ AE = AF (hai cạnh tương ứng)
⇒ ΔAEF cân tại A
⇒
Vì tam giác ABC cân tại A nên (tính chất).
⇒
⇒ FE // BC (có hai góc ở vị trí đồng vị bằng nhau).
⇒ Tứ giác BFEC là hình thang.
Lại có: (tính chất tam giác cân)
Do đó hình thang BFEC là hình thang cân
Vì FE // BC nên ta có: (so le trong)
Lại có: ( vì BE là tia phân giác của góc B)
⇒
⇒ ΔFBE cân ở F ⇒ FB = FE
Bài 29: Hình thang cân ABCD (AB// CD) có = 110o. Khẳng định nào dưới đây là đúng
A. = 120o
B. = 110o
C. = 70o
D. = 60o
Đáp án: C
Giải thích:
Ta có: = 180° (hai góc trong cùng phía)
Suy ra: = 180° - = 180° - 110° =70°
Mà (tính chất hình thang cân)
Nên = 70°
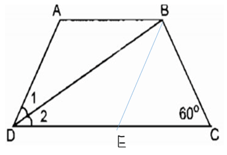
Bài 30: Hình thang cân ABCD có đường chéo BD vuông góc với cạnh bên BC, BD là tia phân giác của-góc D. Tính chu vi của hình thang, biết BC = 3cm.
A. 15cm
B. 9cm
C. 12cm
D. 27cm
Đáp án: A
Giải thích:
Ta có: AD = BC = 3 (cm) (tính chất hình thang cân)
Vì AB // CD nên (so le trong)
Mà (do DB là tia phân giác của góc D )
⇒
Suy ra: ΔABD cân tại A.
⇒ AB = AD = 3 (cm)
Vì ΔBDC vuông tại B nên = 90o
Mà (do ABCD là hình thang cân) và .
Suy ra:
Khi đó; .
Từ B kẻ đường thẳng song song AD cắt CD tại E.
Hình thang ABED có hai cạnh bên song song nên AB = DE và AD = BE
⇒ DE = 3 (cm), BE = 3 (cm)
Mà (đồng vị)
Suy ra:
⇒ΔBEC cân tại B có = 60o
Suy ra: ΔBEC đều
⇒ EC = BC = 3 (cm)
Ta có: CD = CE + ED = 3 + 3 = 6(cm)
Chu vi hình thang ABCD bằng:
AB + BC + CD + DA = 3 + 3 + 6 + 3 = 15 (cm)
Bài 31: Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE. Tứ giác BDEC là hình gì ?
A. Hình thang
B. Hình thang vuông
C. Hình thang cân
D. Hình chữ nhật
Đáp án: C
Giải thích:
Vì AD = AE
⇒ ΔADE cân tại A nên (tính chất tam giác cân)
ΔABC cân tại A ⇒ (tính chất tam giác cân)
Suy ra: mà hai góc này ở vị trí đồng vị
⇒ DE // BC (có cặp góc đồng vị bằng nhau)
Do đó, tứ giác BDEC là hình thang.
Lại có: (tính chất tam giác cân) hay .
Vậy BDEC là hình thang cân.
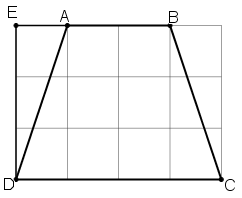
Bài 32:Tính độ dài cạnh AD của hình thang cân ABCD trên giấy kẻ ô vuông (h.30, độ dài của cạnh ô vuông là 1cm).
A. cm
B. 2cm
C. 4cm
D. cm
Đáp án: A
Giải thích:
(Mỗi ô vuông là 1cm).
Ta lấy điểm E như trên hình vẽ.
Quan sát vào hình vẽ ta thấy :
+ AB = 2cm
+ CD = 4cm.
+ Tính AD :
Xét tam giác vuông ADE có AE = 1cm, DE = 3cm:
AD2 = AE2 + DE2 (Định lý Pytago)
AD2 = 12 + 32 = 10
Bài 33: Hình thang cân là hình thang có tính chất nào trong số các tính chất dưới đây?
A. Có bốn cạnh song song với nhau.
B. Có hai đường chéo vuông góc với nhau.
C. Có hai góc kề một đáy bằng nhau.
D. Có bốn cạnh bằng nhau.
Đáp án: C
Giải thích: Trong hình thang cân hai góc kề một cạnh đáy bằng nhau.
Bài 34: Cho hình thang cân ABCD (AB//CD), E là giao điểm của hai đường chéo. Chứng minh rằng
A. AC = CD
B. EA = EB, EC = ED.
C. AB = CD
D.
Đáp án: C
Giải thích:
Do ABCD là hình thang cân nên:
AD = BC;
AC = BD;
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC cạnh chung
⇒ ΔADC = ΔBCD (c.c.c)
⇒ ΔECD cân tại E
⇒ EC = ED.
Mà AC = BD
⇒ AC – EC = BD – ED
hay EA = EB.
Vậy EA = EB, EC = ED.
Bài 35: Chọn đáp án đúng nhất?
A. Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
B. Trong hình thang cân, hai cạnh bên bằng nhau.
C. Trong hình thang cân, hai đường chéo bằng nhau.
D. Cả 3 đáp án còn lại đều đúng.
Đáp án: D
Giải thích:
+ Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
+ Trong hình thang cân, hai cạnh bên bằng nhau.
+ Trong hình thang cân, hai đường chéo bằng nhau.
Vậy cả A, B, C đều đúng
Bài 36: Cho hình thang cân ABCD (như hình vẽ) có . Số đo của
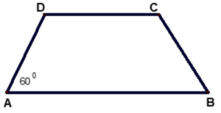
B.
C.
D.
Đáp án: C
Giải thích:
Áp dụng tính chất của hình thang cân ta có:
Bài 37: Một hình thang cân có cạnh bên là 2,5cm; đường trung bình là 3cm. Chu vi của hình thang là:
A. 8cm
B. 12cm
C. 11cm
D. 11,5cm
Đáp án: D
Giải thích:
Tổng độ dài hai đáy là: 3.2 = 6 (cm)
Chu vi hình thang là: 2,5.2 + 6 = 11 (cm)
Đáp án cần chọn là: D
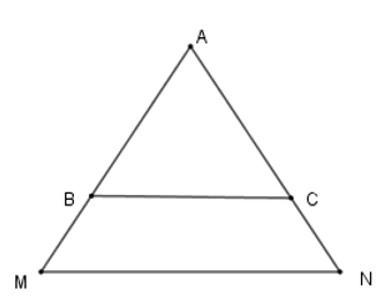
Bài 38: Cho tam giác ΔAMN cân tại A. Các điểm B, C lần lượt trên các cạnh AM, AN sao cho AB = AC. Hãy chọn câu đúng:
A. MB = NC
B. BCNM là hình thang cân
C.
D. Cả A, B, C đều đúng
Đáp án: D
Giải thích:
Xét ΔBAC có: BA = CA (gt) nên ΔBCA là tam giác cân.
Suy ra: 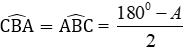
Vì ΔAMN cân tại A ⇒ AM = AN mà AB = AC nên AM – AB = AN – AC ⇔ MB = NC do đó C đúng.
Lại có: 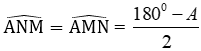
Từ (1) và (2) suy ra:
Mà hai góc 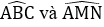
Tứ giác BCNM có: MN // BC (cmt) nên là hình thang.
Hình thang BCNM có: 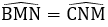
Vậy cả A, B, C đúng
Đáp án cần chọn là: D
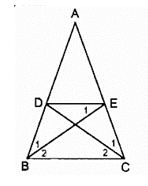
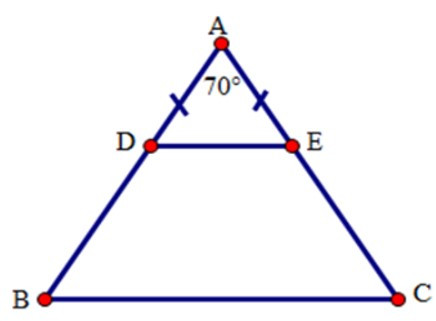
Bài 39: Cho tam giác ABC cân tại A. Gọi D, E theo thứ tự thuộc các cạnh bên AB, AC sao cho DE // BC.
Chọn đáp án đúng nhất. Tứ giác BDEC là hình gì?
A. Hình thang
B. Hình thang vuông
C. Hình thang cân
D. Cả A, B, C đều sai
Đáp án: C
Giải thích:
Tứ giác BDEC có DE // BC nên tứ giác BDEC là hình thang. Lại có 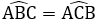
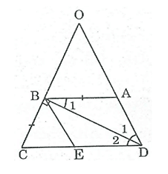
Bài 40: Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC, cắt các cạnh AB, AC lần lượt tại D và E.
Chọn khẳng định đúng.
A. DE > BD + CE
B. DE = BD + CE
C. DE < BD + CE
D. BC = BD + CE
Đáp án: B
Giải thích:
Suy ra tam giác EIC cân đỉnh E
Do đó EI = EC (2)
Cộng (1) và (2) vế theo vế ta được: DI + EI = BD + CE
⇒ DE = BD + CE
Các câu hỏi trắc nghiệm Toán lớp 8 có đáp án, chọn lọc khác:
Trắc nghiệm Đường trung bình của tam giác, của hình thang có đáp án
Trắc nghiệm Đối xứng trục có đáp án
Trắc nghiệm Hình bình hành có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Sinh học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Toán lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Hóa học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn lớp 11 có đáp án
- Trắc nghiệm Tiếng Anh lớp 11 có đáp án
- Trắc nghiệm Vật Lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Địa lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm GDCD lớp 11 có đáp án
- Trắc nghiệm Lịch sử lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Công nghệ lớp 11 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 11 có đáp án
- Trắc nghiệm Tin học lớp 11 có đáp án
- Trắc nghiệm Toán lớp 12 có đáp án
- Trắc nghiệm Sinh học lớp 12 có đáp án
- Trắc nghiệm Hóa học lớp 12 có đáp án
- Trắc nghiệm Ngữ văn lớp 12 có đáp án
- Trắc nghiệm Tiếng Anh lớp 12 có đáp án
- Trắc nghiệm Địa lí lớp 12 có đáp án
- Trắc nghiệm Vật Lí lớp 12 có đáp án
- Trắc nghiệm Công nghệ lớp 12 có đáp án
- Trắc nghiệm Giáo dục công dân lớp 12 có đáp án
- Trắc nghiệm Lịch sử lớp 12 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 12 có đáp án