TOP 40 câu Trắc nghiệm Đối xứng trục (có đáp án 2023) - Toán 8
Bộ 40 câu hỏi trắc nghiệm Toán lớp 8 Bài 6: Đối xứng trục có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 8 Bài 6.
Trắc nghiệm Toán 8 Bài 6: Đối xứng trục
Bài giảng Trắc nghiệm Toán 8 Bài 6: Đối xứng trục
Bài 1: Hãy chọn câu sai.
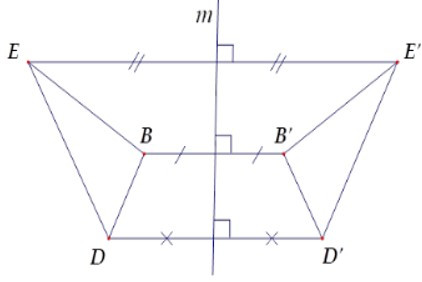
A. Hai đoạn thẳng EB và E’B’ đối xứng nhau qua m.
B. Hai đoạn thẳng DB và D’B’ đối xứng nhau qua m.
C. Hai tam giác DEB và D’E’B’ đối xứng nhau qua m
D. Hai đoạn thẳng DE và D’B’ đối xứng nhau qua m.
Đáp án: D
Giải thích:
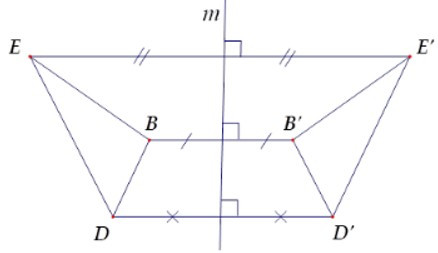
Từ hình vẽ ta có A và A’ đối xứng nhau qua đường thẳng m; B và B’ đối xứng nhau qua đường thẳng m; C và C’ đối xứng nhau qua đường thẳng m.
Suy ra hai đoạn thẳng EB và E’B’ đối xứng nhau qua m.
Hai đoạn thẳng DB và D’B’ đối xứng nhau qua m.
Hai tam giác DEB và D’E’B’ đối xứng nhau qua m.
Hai đoạn thẳng DE và D’E’ đối xứng nhau qua m nên D sai.
Bài 2: Hãy chọn câu đúng. Trục đối xứng của hình thang cân là:
A. Đường thẳng đi qua trung điểm hai cạnh bên của hình thang cân
B. Đường chéo của hình thang cân
C. Đường thẳng vuông góc với hai đáy của hình thang cân
D. Đường thẳng đi qua trung điểm hai đáy của hình thang cân
Đáp án: D
Giải thích:
Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.
Bài 3: Cho ΔABC và ΔA’B’C’ đối xứng nhau qua đường thẳng d biết AB = 8cm, BC = 11cm và chu vi của tam giác ABC = 30 cm. Khi đó độ dài cạnh C’A’ của tam giác A’B’C’ là:
A. 16cm
B. 15cm
C. 8cm
D. 11cm
Đáp án: D
Giải thích:
+ Xét tam giác ABC có
chu vi PABC = AB + AC + BC
=> PABC = 11cm.
+ Vì tam giác ABC và tam giác A’B’C’ đối xứng nhau qua đường thẳng d
nên AC = A’C’ = 11cm
Bài 4: Hãy chọn câu đúng?
A. Tam giác đều có ba trục đối xứng
B. Tam giác cân có hai trục đối xứng
C. Hình tam giác có ba trục đối xứng
D. Hình thang cân có hai trục đối xứng
Đáp án: A
Giải thích:
+ Hình thang cân có trục đối xứng là đường thẳng đi qua trung điểm hai đáy nên hình thang cân có một trục đối xứng. Do đó A sai.
+ Tam giác cân có một trục đối xứng là đường trung trực hạ từ đỉnh cân nên B sai.
+ Tam giác thường thì không có trục đối xứng nên C sai.
+ Tam giác đều có ba trục đối xứng là ba đường trung trực của tam giác nên D đúng.
Bài 5: Cho hình vuông ABCD cạnh bằng a. M và N là hai điểm lưu động lần lượt trên cạnh AB và AD sao cho ^MCNˆMCN = 450. Vẽ tia Cx vuông góc với CN, Cx cắt đường thẳng AB tại E.
1. Chọn kết luận đúng nhất.
A. E là điểm đối xứng của N qua CM
B. Tam giác CEN là tam giác cân tại C
C. Cả A, B đều đúng
D. Cả A, B đều sai
Đáp án: C
Giải thích:
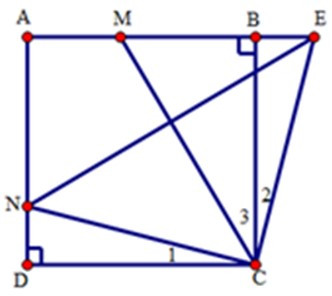
Ta có CN ⊥ CE (gt)
mà ^MCNˆMCN = 450 nên ^MCEˆMCE = 450 hay ^C2+^C3ˆC2+ˆC3 = 450
Mà ^C1+^C3ˆC1+ˆC3 = 450 (vì ^MCNˆMCN = 450) nên ^C1=^C2ˆC1=ˆC2
Xét tam giác CDN và tam giác CBE có:
BC = DC (do ABCD là hình vuông);
ˆB=ˆDˆB=ˆD = 900;
^C1=^C2ˆC1=ˆC2 (cmt)
Suy ra ΔCDN = ΔCBE (g.c.g)
Suy ra CN = CE
Xét tam giác CEN có CN = CE (cmt) nên tam giác CEN là tam giác cân tại C
Suy ra phân giác CM đồng thời là đường trung trực của NE.
Vậy E là điểm đối xứng của N qua CM
2. Tính chu vi của tam giác AMN theo a.
A. 4a
B. 3a
C. a
D. 2a
Đáp án: D
Giải thích:
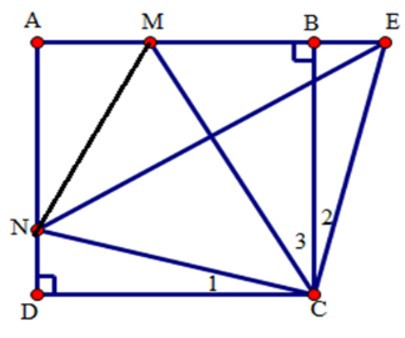
Ta có: ΔCMN = ΔCME (do tính đối xứng qua CM)
Nên MN = ME
Suy ra chu vi tam giác AMN là:
AM + AN + MN
= AM + AN + ME
= AM + AN + MB + BE
= AM + AN + MB + ND
(vì ΔCDN = ΔCBE (theo câu trước) nên BE = ND)
= (AM + MB) + (AN + ND)
Vậy chu vi tam giác AMN bằng 2a.
Bài 6: Cho tam giác ABC cân tại B, các đường trung tuyến AA’, BB’, CC’.
Trục đối xứng của tam giác ABC là:
A. AA’
B. BB’
C. AA’ và CC’
D. CC’
Đáp án: B
Giải thích:
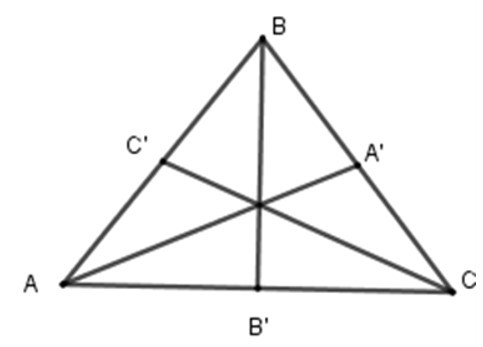
Do tam giác ABC cân tại B, nên đường trung tuyến BB’ đồng thời là đường trung trực.
Do đó BB’ là trục đối xứng của tam giác ABC.
Bài 7: Cho hình vẽ. Hãy chọn câu đúng:
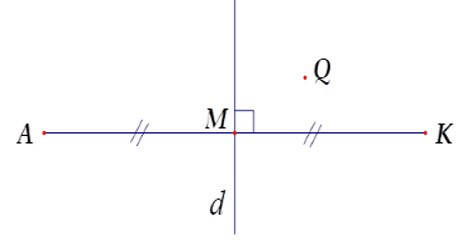
A. Điểm đối xứng với A qua đường thẳng d là A.
B. Điểm đối xứng với K qua đường thẳng d là K
C. Điểm đối xứng với A qua đường thẳng d là K
D. Điểm đối xứng với Q qua đường thẳng d là Q.
Đáp án: C
Giải thích:
Từ hình vẽ ta có đường thẳng d là đường trung trực của đoạn thẳng AK nên điểm đối xứng với A qua đường thẳng d là K.
Bài 8: Cho tam giác ABC cân tại A, các đường trung tuyến AA’, BB’, CC’. Trục đối xứng của tam giác ABC là:
A. AA’
B. BB’
C. AA’ và CC’
D. CC’
Đáp án: A
Giải thích:
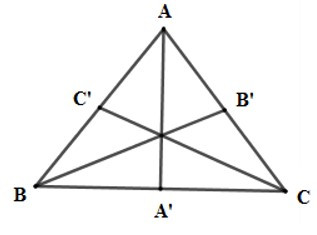
Do tam giác ABC cân tại A, nên đường trung tuyến AA’ đồng thời là đường trung trực.
Do đó AA’ là trục đối xứng của tam giác ABC.
Bài 9: Cho tam giác ABC, trong đó AB = 11cm, AC = 15cm. Vẽ hình đối xứng với tam giác ABC qua trục là cạnh BC. Chu vi của tứ giác tạo thành là:
A. 52cm
B. 54cm
C. 26cm
D. 51cm
Đáp án: A
Giải thích:
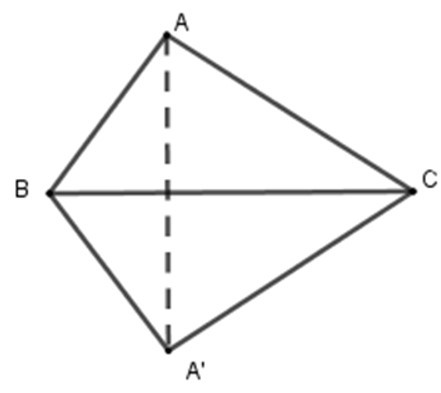
Gọi A’ là điểm đối xứng với A qua BC. Khi đó tam giác A’BC đối xứng với tam giác ABC qua BC.
Tứ giác tạo thành là ABCA’.
Ta có A’B = AB = 11cm (vì A’B và AB đối xứng nhau qua BC)
A’C = AC = 15cm (vì A’C và AC đối xứng nhau qua BC)
Chu vi tứ giác ABCA’ là
P = AB + AC + A’B + A’C
= 11 + 15 + 11 + 15 = 52 cm
Bài 10: Hãy chọn câu đúng.
A. Hình thang cân có trục đối xứng là đường trung trực của hai đáy
B. Tam giác có trục đối xứng là đường trung tuyến
C. Tam giác có trục đối xứng là đường cao
D. Hình thang vuông có đối xứng là đường trung bình của nó
Đáp án: A
Giải thích:
Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.
Như vậy hình thang cân có trục đối xứng là đường trung trực của hai đáy.
Bài 11: Cho đoạn thẳng AB có độ dài 3cm và đường thẳng d. Đoạn thẳng A’B’ đối xứng với AB qua d. Độ dài đoạn thẳng A’B’ là:
A. 3cm
B. 6cm
D. 9cm
D. 12cm
Đáp án: A
Giải thích:
Vì đoạn thẳng A’B’ đối xứng với AB
qua d nên A’B’ = AB = 3cm.
Bài 12: Hãy chọn câu sai:
A. Nếu hai góc đối xứng nhau qua một đường thẳng thì chúng bằng nhau
B. Nếu hai tam giác đối xứng nhau qua một đường thẳng thì chúng bằng nhau
C. Nếu hai tam giác đối xứng nhau qua một đường thẳng thì chu vi của chúng bằng nhau.
D. Nếu hai tia đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.
Đáp án: D
Giải thích:
Vì hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng
thì chúng bằng nhau nên D sai.
Bài 13: Cho đoạn thẳng AB có độ dài 6cm và đường thẳng d. Đoạn thẳng A’B’ đối xứng với AB qua d. Độ dài đoạn thẳng A’B’ là:
A. 3cm
B. 6cm
D. 9cm
D. 12cm
Đáp án: B
Giải thích:
Vì đoạn thẳng A’B’ đối xứng với AB
qua d nên A’B’ = AB = 6cm.
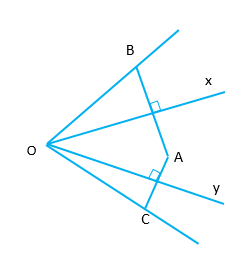
Bài 14: Trên tia phân giác góc ngoài tại đỉnh C của tam giác ABC, lấy điểm M (M khác C). Chọn câu đúng.
A. MA + MB = AC + BC
B. MA + MB > AC + BC
C. MA + MB < AC + BC
D. Chưa đủ điều kiện để so sánh
Đáp án: B
Giải thích:
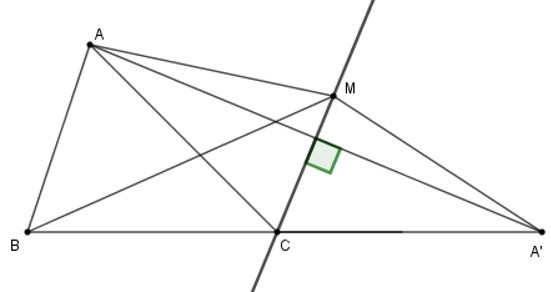
Trên tia đối của tia CB lấy điểm A’ sao cho CA = CA’
Khi đó ta có: ΔCAA’ cân tại A có CM là phân giác
góc ACA’ nên CM cũng là đường trung trực của AA’.
Từ đó ta có: MA = MA’
Nên MA + MB = MA’ + MB
Xét tam giác MA’B có MA’ +MB > A’B ó MA + MB > A’C + BC
Hay MA + MB > AC + BC (vì CA = CA’)
Bài 15: Cho hình vẽ. Hãy chọn câu sai.
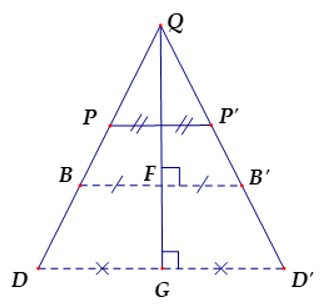
A. Điểm đói xứng với P qua đường thẳng QG là P’.
B. Điểm đối xứng với B qua đường thẳng QG là B’.
C. Điểm đối xứng với D qua đường thẳng QG là G.
D. Điểm đối xứng với G qua đường thẳng QG là G
Đáp án: C
Giải thích:
Từ hình vẽ ta có đường thẳng QG là đường trung trực của đoạn thẳng DD’, BB’, PP’ nên
Điểm đối xứng với P qua đường thẳng QG là P’ nên B đúng.
ĐIểm đối xứng với B qua đường thẳng QG là B’ nên B đúng.
Điểm đối xứng với D qua đường thẳng QG là D’ nên C sai.
Vì G Є QG nên điểm đối xứng với G qua QG là G nên D đúng.
Bài 16: Cho hình vẽ, AD = AE, AG là trung trực của DE. Có bao nhiêu cặp đoạn thẳng đối xứng nhau qua trục AG (các đoạn thẳng thuộc đường thẳng AD, AE)? Chọn câu đúng.
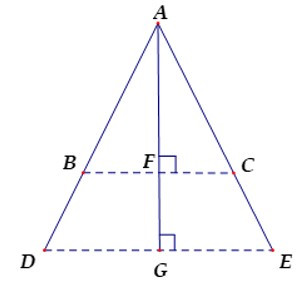
A. 1
B. 2
C. 3
D. 4
Đáp án: C
Giải thích:
Từ giả thiết ta thấy ΔADE cân tại A có AG là đường cao nên AG cũng là đường trung trực của DE.
Nên điểm D và E đối xứng nhau qua AG.
Lại có BC // DE (cùng vuông với AG)
nên suy ra ABCD=ACAEABCD=ACAE (định lý Ta-lét)
Mà AD = AE (gt) => AB = AC
Do đó ΔABC cân tại A có AF là đường cao nên AF cũng là đường trung trực của BC.
Từ đó điểm B, C đối xứng nhau qua AG.
Như vậy:
+ Hai đoạn thẳng BD, CE đối xứng nhau qua AG.
+ Hai đoạn thẳng AB, AC đối xứng nhau qua AG
+ Hai đoạn thẳng AD, AE đối xứng nhau qua AG
Bài 17: Cho ΔABC và ΔA’B’C’ đối xứng nhau qua đường thẳng d biết AB = 4cm, BC = 7cm và chu vi của tam giác ABC = 17cm. Khi đó độ dài cạnh C’A’ của tam giác A’B’C’ là:
A. 17cm
B. 6cm
C. 7cm
D. 4cm
Đáp án: B
Giải thích:
+ Xét tam giác ABC có chu vi
PABC = AB + AC + BC
=> PABC = 6cm.
+ Vì tam giác ABC và tam giác A’B’C’ đối xứng nhau qua
đường thẳng d nên AC = A’C’ = 6cm
Bài 18: Cho tam giác ABC, trong đó AB = 8cm, AC = 10cm. Vẽ hình đối xứng với tam giác ABC qua trục là cạnh BC. Chu vi của tứ giác tạo thành là:
A. 38cm
B. 54cm
C. 36cm
D. 18cm
Đáp án: C
Giải thích:
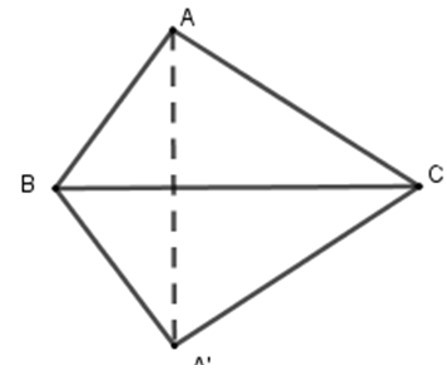
Gọi A’ là điểm đối xứng với A qua BC.
Khi đó tam giác A’BC đối xứng với tam giác ABC qua BC.
Tứ giác tạo thành là ABCA’.
Ta có A’B = AB = 8cm (vì A’B và AB đối xứng nhau qua BC)
A’C = AC = 10cm (vì A’C và AC đối xứng nhau qua BC)
Chu vi tứ giác ABCA’ là
P = AB + AC + A’B + A’C = 8 + 10 + 8 + 10 = 36 cm
Bài 19: Cho hai điểm A, B nằm trên cùng một nửa mặt phẳng bờ là đường thẳng d. Gọi B’ là điểm đối xứng của B qua đường thẳng d. Tìm trên đường thẳng d điểm M sao cho tổng MA + MB nhỏ nhất. Chọn khẳng định đúng nhất.
A. M là giao điểm của đoạn thẳng AB và đoạn thẳng d.
B. M là giao điểm của đoạn AB’ và đường thẳng d.
C. Cả A, B đều đúng.
D. Cả A, B đều sai.
Đáp án: B
Giải thích:
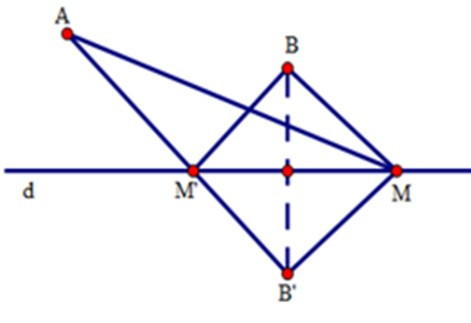
Gọi B’ là điểm đối xứng của B qua đường thẳng d. B’ cố định.
Ta có: MB = MB’ (tính chất đối xứng trục).
Xét ba điểm M, A, B’ ta có MA + MB’ ≥ AB’
Do đó MA + MB ≥ AB’
Dấu “=” xảy ra khi và chỉ khi A, M, B thẳng hang theo thứ tự đó
hay M là giao điểm của đoạn AB’ và đường thẳng d.
Vậy khi M ≡ M’ là giao điểm của đoạn thẳng AB’ và đường thẳng d
thì tổng MA + MB nhỏ nhất, trong đó B’ là điểm đối xứng của B qua d.
Bài 20: Cho tam giác ABC có ˆAˆA = 200; ˆBˆB = 800, d là trung trực của cạnh AB. Trên cạnh AC, lấy điểm M sao cho AM = BC và gọi M’ là điểm đối xứng của M qua d. Tam giác M’BC là tam giác gì? Chọn đáp án đúng nhất.
A. đều
B. cân tại B
C. cân tại C
D. vuông cân tại M’
Đáp án: A
Giải thích:
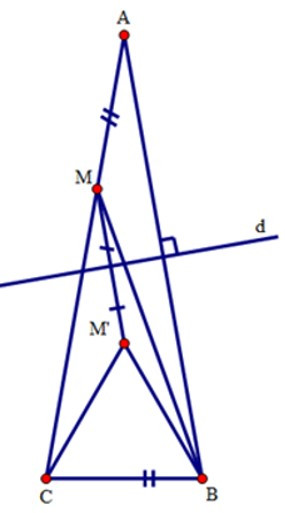
Do tính chất đối xứng qua d, ta có AM = BM’
Mà AM = BC (gt) nên BM’ = BC
Ta lại có: ^M'BA=^MABˆM'BA=ˆMAB (do MA đối xứng với M’B qua d)
Suy ra ^M'BCˆM'BC = ˆBˆB– 200
= 800 – 200 = 600
Xét tam giác M’BC có BM’ = BC, ^M'BCˆM'BC = 600 do đó tam giác M’BC là tam giác đều
Bài 21: Cho tam giác ABC có = 200; = 800, d là trung trực của cạnh AB. Trên cạnh AC, lấy điểm M sao cho AM = BC và gọi M’ là điểm đối xứng của M qua d. Tính góc BMC.
A. 450
B. 300
C. 600
D. 400
Đáp án: B
Giải thích:
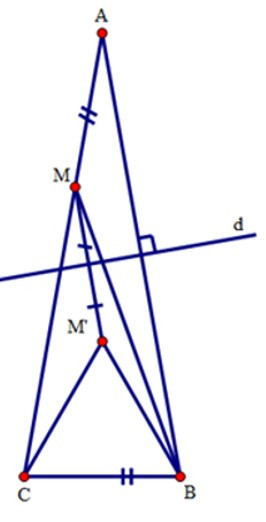

Bài 22: Chọn phương án đúng nhất trong các phương án sau
A. Đường thẳng đi qua hai đáy của hình thang là trục đối xứng của hình thang đó.
B. Đương thẳng đi qua hai đáy của hình thang cân là trục đối xứng của hình thang cân.
C. Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.
D. Cả A, B, C đều sai.
Đáp án: C
Giải thích:
Định lí: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang đó.
Bài 23: Cho đoạn thẳng AB có độ dài là 5cm và đường thẳng d, đoạn thẳng A'B' đối xứng với AB qua d, khi đó độ dài của A'B' là ?
A. 3cm
B. 5cm
C. 9cm
D. 12cm
Đáp án: A
Giải thích:
Tính chất: Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.
Khi đó AB = A'B' = 5cm
Bài 24: Tam giác ABC đối xứng với tam giác A'B'C' qua đường thẳng d, biết chu vi của tam giác ABC là 56cm thì chu vi của tam giác A'B'C' là ?
A. 24cm
B. 32cm
C. 40cm
D. 56cm
Đáp án: D
Giải thích:
Tính chất: Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.
Khi đó ta có: PABC = PA'B'C' = 56( cm )
Bài 25: Hãy chọn câu đúng. Trục đối xứng của hình thang cân là:
A. Đường thẳng đi qua trung điểm hai cạnh bên của hình thang cân
B. Đường chéo của hình thang cân
C. Đường thẳng vuông góc với hai đáy của hình thang cân
D. Đường thẳng đi qua trung điểm hai đáy của hình thang cân
Đáp án: D
Giải thích:
Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.
Bài 26: Hãy chọn câu đúng.
A. Hình thang cân có trục đối xứng là đường trung trực của hai đáy
B. Tam giác có trục đối xứng là đường trung tuyến
C. Tam giác có trục đối xứng là đường cao
D. Hình thang vuông có đối xứng là đường trung bình của nó
Đáp án: A
Giải thích:
Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.
Như vậy hình thang cân có trục đối xứng là đường trung trực của hai đáy.
Bài 27: Hãy chọn câu đúng?
A. Tam giác đều có ba trục đối xứng
B. Tam giác cân có hai trục đối xứng
C. Hình tam giác có ba trục đối xứng
D. Hình thang cân có hai trục đối xứng
Đáp án: A
Giải thích:
+ Hình thang cân có trục đối xứng là đường thẳng đi qua trung điểm hai đáy nên hình thang cân có một trục đối xứng. Do đó A sai.
+ Tam giác cân có một trục đối xứng là đường trung trực hạ từ đỉnh cân nên B sai.
+ Tam giác thường thì không có trục đối xứng nên C sai.
+ Tam giác đều có ba trục đối xứng là ba đường trung trực của tam giác nên D đúng.
Bài 28: Cho Δ ABC có Aˆ = 500, điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua AC. Tính số đo góc DAEˆ = ?
A. 450
B. 600
C. 1000
D. 800
Đáp án: C
Giải thích:
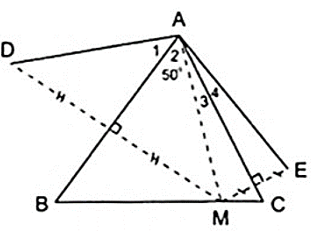
a) Theo giả thiết ta có:
+ D đối xứng với M qua AB.
+ E đối xứng với M qua AC.
+ A đối xứng với A qua AB, AC.
⇒ AD đối xứng với AM qua AB, AE đối xứng với AM qua AC.
Áp dụng tính chất đối xứng ta có: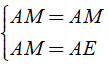 ⇒ AD = AE ⇒ (đpcm).
⇒ AD = AE ⇒ (đpcm).
b) Theo ý câu a, ta có
+ A1ˆ đối xứng A2ˆ qua AB
+ A3ˆ đối xứng A4ˆ qua AC.
Áp dụng tính chất đối xứng trục, ta có:
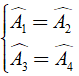 ⇒ A1ˆ + A4ˆ = A2ˆ + A3ˆ = Aˆ = 500 ⇒ DAEˆ = 2Aˆ = 1000.
⇒ A1ˆ + A4ˆ = A2ˆ + A3ˆ = Aˆ = 500 ⇒ DAEˆ = 2Aˆ = 1000.
Vậy DAEˆ = 1000.
Bài 29: Tam giác ABC đối xứng với tam giác A'B'C' qua đường thẳng d, biết chu vi của tam giác ABC là 48cm thì chu vi của tam giác A'B'C' là ?
A. 24cm
B. 32cm
C. 40cm
D. 48cm
Đáp án: A
Giải thích:
Vì tam giác ABC đối xứng với tam giác A’B’C’ qua O nên ΔABC = ΔA’B’C’
=> AB = A’B’; AC = A’C’; BC = B’C’
Nên AB + AC + BC = A’B’ + A’C’ + B’C’
=> PABC = PA’B’C’
Do đó chu vi tam giác A'B'C' là PA'B'C' = 48cm
Đáp án cần chọn là: D
Bài 30:Tam giác ABC đối xứng với tam giác A’B’C’ qua O. Biết chu vi của tam giác A’B’C’ là 40cm. Chu vi của tam giác ABC là:
A. 24cm
B. 32cm
C. 40cm
D. 48cm
Đáp án: C
Giải thích:
Vì tam giác ABC đối xứng với tam giác A’B’C’ qua O nên ΔABC = ΔA’B’C’
=> AB = A’B’; AC = A’C’; BC = B’C’
Nên AB + AC + BC = A’B’ + A’C’ + B’C’
=> PABC = PA’B’C’
Do đó chu vi tam giác ABC là PABC = 40cm
Đáp án cần chọn là: B
Bài 31: Đường tròn là hình
A. không có trục đối xứng.
B. có một trục đối xứng.
C. có hai trục đối xứng.
D. có vô số trục đối xứng.
Đáp án: D
Giải thích: Đường tròn là hình có vô số trục đối xứng.
Bài 32:
Cho tam giác ABC và tam giác A'B'C' đối xứng với nhau qua điểm I biết AB = 4cm, AC = 8cm và chu vi của tam giác ABC bằng 22cm. Hỏi độ dài cạnh B'C' của tam giác A'B'C' là?
A. B'C' = 9cm
B. B'C' = 8cm
C. B'C' = 4cm
D. B'C' = 10cm
Đáp án: D
Giải thích:
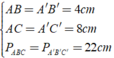
⇒ BC = B'C' = 22 - 8 - 4 = 10( cm )
Bài 33: Cho đoạn thẳng AB có độ dài là 3cm và đường thẳng d, đoạn thẳng A'B' đối xứng với AB qua d, khi đó độ dài của A'B' là ?
A. 3cm
B. 6cm
C. 9cm
D. 12cm
Đáp án: A
Giải thích:
Tính chất: Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.
Khi đó AB = A'B' = 3cm.
Bài 34: Chọn phương án đúng nhất trong các phương án sau
A. Đường thẳng đi qua hai đáy của hình thang là trục đối xứng của hình thang đó.
B. Đương thẳng đi qua hai đáy của hình thang cân là trục đối xứng của hình thang cân.
C. Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.
D. Cả A, B, C đều sai.
Đáp án: C
Giải thích:
Định lí: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang đó.
Bài 35: Hình chữ nhật có hai kích thước khác nhau thì có số trục đối xứng là
A. 0.
B. 1.
C. 2.
D. 3.
Đáp án: A
Giải thích: Hình chữ nhật có hai kích thước khác nhau thì có 2 trục đối xứng là các đường thẳng nối trung điểm hai cạnh đối diện.
Bài 36:Trong các tứ giác sau, tứ giác nào là hình có (4 ) trục đối xứng?
A. Hình chữ nhật
B. Hình vuông
C. Hình bình hành
D. Hình thoi
Đáp án: B
Giải thích:
* Hình chữ nhật:
- Hình chữ nhật có 22 trục đối xứng (đó là đường trung trực của chiều dài và chiều rộng).
* Hình vuông:
Hình vuông có 44 trục đối xứng.
* Hình bình hành:
- Hình bình hành không có trục đối xứng.
* Hình thoi:
- Hình thoi có hai trục đối xứng là hai đường chéo
Bài 37: Trong các tứ giác sau, tứ giác nào là hình có (4 ) trục đối xứng?
A. Hình chữ nhật
B. Hình vuông
C. Hình bình hành
D. Hình thoi
Đáp án: C
Giải thích:
- Hình chữ nhật có 22 trục đối xứng (đó là đường trung trực của chiều dài và chiều rộng).
Hình vuông có 44 trục đối xứng.
- Hình bình hành không có trục đối xứng.
- Hình thoi có hai trục đối xứng là hai đường chéo
Bài 38: Cho góc xOy =40o=40o, điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, điểm C đối xứng với A qua Oy. Ta tính số đo góc BOC là:
A. 800800
B. 10001000
C. 700700
D. 11001100
Bài 39:
Trong các biển báo giao thông sau đây, có mấy biển có trục đối xứng?

A. 1
B. 2
C. 3
D. 4
Đáp án: C
Giải thích:
Các hình có trục đối xứng đó là : Hình a, hình b, hình d.
Bài 40: Cho tam giác ABC cân tại A, đường cao AH. Tìm hình đối xứng với canh AB của tam giác ABC qua AH.
A. AC
B. BH
C. CH
D. BC
Đáp án: A
Giải thích:
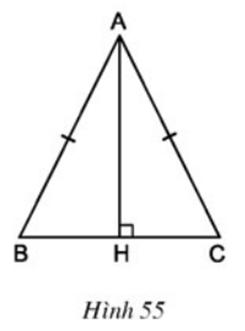
AB đối xứng với AC qua AH BC đối xứng với CB qua AH
Các câu hỏi trắc nghiệm Toán lớp 8 có đáp án, chọn lọc khác:
Trắc nghiệm Hình bình hành có đáp án
Trắc nghiệm Đối xứng tâm có đáp án
Trắc nghiệm Hình chữ nhật có đáp án
Trắc nghiệm Đường thẳng song song với một đường thẳng cho trước có đáp án
Trắc nghiệm Hình thoi có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Sinh học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Toán lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Hóa học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn lớp 11 có đáp án
- Trắc nghiệm Tiếng Anh lớp 11 có đáp án
- Trắc nghiệm Vật Lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Địa lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm GDCD lớp 11 có đáp án
- Trắc nghiệm Lịch sử lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Công nghệ lớp 11 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 11 có đáp án
- Trắc nghiệm Tin học lớp 11 có đáp án
- Trắc nghiệm Toán lớp 12 có đáp án
- Trắc nghiệm Sinh học lớp 12 có đáp án
- Trắc nghiệm Hóa học lớp 12 có đáp án
- Trắc nghiệm Ngữ văn lớp 12 có đáp án
- Trắc nghiệm Tiếng Anh lớp 12 có đáp án
- Trắc nghiệm Địa lí lớp 12 có đáp án
- Trắc nghiệm Vật Lí lớp 12 có đáp án
- Trắc nghiệm Công nghệ lớp 12 có đáp án
- Trắc nghiệm Giáo dục công dân lớp 12 có đáp án
- Trắc nghiệm Lịch sử lớp 12 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 12 có đáp án