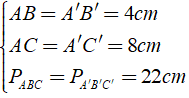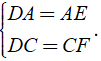TOP 40 câu Trắc nghiệm Đối xứng tâm (có đáp án 2023) - Toán 8
Bộ 40 câu hỏi trắc nghiệm Toán lớp 8 Bài 8: Đối xứng tâm có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 8 Bài 8.
Trắc nghiệm Toán 8 Bài 8: Đối xứng tâm
Bài giảng Trắc nghiệm Toán 8 Bài 8: Đối xứng tâm
Bài 1: Cho hình bình hành ABEF. Gọi O là giao điểm của AE và BF. Trong các khẳng định sau:
1. E và A đối xứng nhau qua O
2. B và F đối xứng nhau qua O
3. E và F đối xứng nhau qua O
4. AB và EF đối xứng nhau qua O.
Có bao nhiêu khẳng định đúng?
A. 1
B. 2
C. 3
D. 4
Đáp án: C
Giải thích:
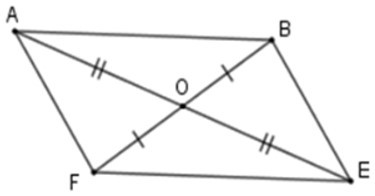
Hình bình hành ABCD có OA = OE; OB = OF nên
+ E và A đối xứng nhau qua O
+ B và F đối xứng nhau qua O
+ AB và EF đối xứng nhau qua O
Nhưng E và F không đối xứng nhau qua O vì OE ≠ OF; O không thuộc EF.
Vậy có 3 khẳng định đúng.
Bài 2: Hãy chọn câu sai:
A. Điểm đối xứng với điểm M qua M cũng chính là điểm M
B. Hai điểm A và B gọi là đói xứng với nhau qua điểm O kkhi O là trung điểm của đoạn thẳng AB
C. Hình bình hành có một tâm đối xứng
D. Đoạn thẳng có hai tâm đối xứng
Đáp án: D
Giải thích:
+ Theo định nghĩa hai điểm đói xứng nhau qua một điểm: Hai điểm A, B gọi là đối xứng với nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó nên B đúng.
+ Trung điểm của đoạn thẳng là tâm đối xứng duy nhất của đoạn thẳng đó nên D sai.
+ Hình bình hành có một tâm đối xứng là giao hai đường chéo nên C đúng.
Điểm đối xứng của một điểm M qua chính M chính là M nên A đúng.
Bài 3: Hãy chọn câu đúng. Cho hình bình hành ABCD. Lấy điểm E thuộc tia đối của tia AD sao cho AD = AE, lấy F thuộc tia đối của tia CD sao cho CD = CF. Hình bình hành ABCD có them điều kiện gì để E đối xứng với F qua đường thẳng DB?
A. AC = DB
B. ˆA = 900
C. AC ⊥ DB
D. ˆD = 900
Đáp án: C
Giải thích:
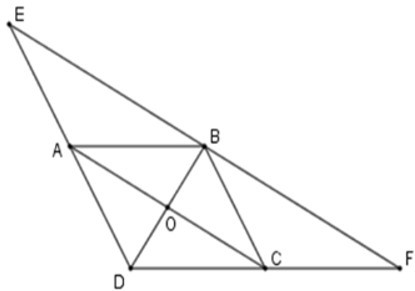
Gọi O là giao điểm hai đường chéo của hình bình hành ABCD
khi đó OA = OC; OB = OD
Xét tam giác DBE ta có OA là đường trung bình
nên OA // EB; OA =12EB (1)
Tương tự OC là đường trung bình của tam giác BDF
=> OC // BF; OC=12 FB (2)
Từ (1); (2) => E, B, F thẳng hàng và EB = BF
(vì OA = OC) hay E đối xứng với F qua điểm B.
Để E đối xứng với F qua đường thẳng BD ta cần them điều kiện EF ⊥ BD.
Mà AC là đường trung bình của tam giác DEF nên AC // EF suy ra BD ⊥ AC.
Vậy hình bình hành ABCD có them điều kiện hai đường chéo vuông góc thì E đối xứng với F qua đường thẳng DB.
Bài 4: Hãy chọn câu sai:
A. Hình bình hành có tâm đối xứng là giao điểm của hai đường chéo
B. Đường tròn có tâm đối xứng chính là tâm của đường tròn
C. Hình thang có tâm đối xứng là giao điểm của hai đường chéo
D. Hình vuông có tâm đối xứng là giao điểm hai đường chéo
Đáp án: C
Giải thích:
+ Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó nên A đúng
+ Đường tròn là hình có hình có tâm đối xứng là tâm của đường tròn nên B đúng.
+ Giao điểm hai đường chéo của hình vuông là tâm đối xứng của hình vuông đó nên D đúng.
+ Hình thang không có tâm đối xứng nên C sai
Bài 5: Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. O là một điểm bất kì nằm trong tứ giác ABCD. Gọi E, F, G, H theo thứ tự là điểm đối xứng với O qua M, N, P, Q.
1. Tứ giác MNPQ là hình gì?
A. Hình thang
B. Hình bình hành
C. Hình thang cân
D. Hình thang vuông
Đáp án: B
Giải thích:
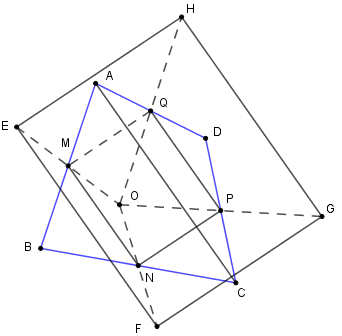
+ Nối AC.
Xét tam giác DAC có QP là đường trung bình nên
QP // AC; QP = 12AC (1)
Xét tam giác BAC có MN là đường trung bình nên
MN // AC; MN =12 AC (2)
Từ (1) và (2) suy ra MN = PQ = (= 12AC);
MN // PQ nên tứ giác MNPQ là hình bình hành.
2. Tứ giác EFGH là hình gì?
A. Hình thang
B. Hình bình hành
C. Hình thang cân
D. Hình thang vuông
Đáp án: B
Giải thích:
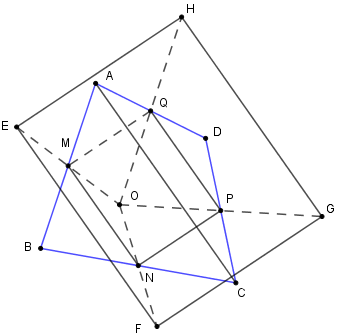
Vì E, F, G, H theo thứ tự là điểm đối xứng với O qua M, N, P, Q nên M, N, P, Q lần lượt là trung điểm của các đoạn thẳng OE, OF, OH, OG.
Xét tam giác OEF có MN là đường trung bình nên
MN // EF; EF = 2MN (*)
Xét tam giác OHG có QP là đường trung bình nên
QP // HG; HG = 2QP (**)
Mà MN = QP (theo câu trước) nên từ (*) và (**)
suy ra EF // HG; EF = HG
Tứ giác EFGH có EF // HG; EF = HG nên EFGH là hình bình hành (dhnb)
Bài 6: Tam giác ABC đối xứng với tam giác A’B’C’ qua O. Biết chu vi của tam giác A’B’C’ là 40cm. Chu vi của tam giác ABC là:
A. 32dm
B. 40cm
C. 20dm
D. 80dm
Đáp án: B
Giải thích:
Vì tam giác ABC đối xứng với tam giác A’B’C’
qua O nên ΔABC = ΔA’B’C’
=> AB = A’B’; AC = A’C’; BC = B’C’
Nên AB + AC + BC = A’B’ + A’C’ + B’C’
=> PABC = PA’B’C’
Do đó chu vi tam giác ABC là PABC = 40cm
Bài 7: Hình bình hành ABCD có tâm đối xứng là:
A. Điểm A
B. Điểm B
C. Giao điểm hai đường chéo
D. Hình bình hành ABCD không có tâm đối xứng
Đáp án: C
Giải thích:
+ Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó nên C đúng
Bài 8: Cho tam giác ABC, đường cao AH, trong đó BC = 30cm, AH = 18cm. Vẽ hình đối xứng với tam giác ABC qua trung điểm của cạnh BC. Diện tích của tam giác tạo thành là:
A. 270cm2
B. 540cm2
C. 280cm2
D. 360cm2
Đáp án: A
Giải thích:
Gọi tam giác A’CB đối xứng với tam giác ABC qua trung điểm cạnh BC. Khi đó ΔABC = ΔA’CB
Nên SABC = SA’BC.
Ta có SABC = 12AH.BC
=12 .18.30 = 270 cm2
nên SA’BC = 270cm2
Bài 9: Cho tam giác ABC có trung tuyến AM. Gọi D, E, F lần lượt là trung điểm của AB, AM, AC. Chọn câu đúng.
A. Điểm A và M đối xứng nhau qua E
B. Điểm D và F đối xứng nhau qua E
C. Cả A, B đều đúng
D. Cả A, B đều sai
Đáp án: C
Giải thích:

Vì E là trung điểm của AM nên A, M đối xứng nhau qua E
Xét tam giác ABM có DE là đường trung bình nên DE = 12BM (1)
Xét tam giác ACM có EF là đường trung bình nên EF = 12MC (2)
Mà MB = MC nên từ (1) và (2) ta suy ra DE = EF hay E là trung điểm đoạn DF.
Do đó D; F đối xứng nhau qua E.
Bài 10: Điền từ thích hợp vào chỗ trống. Hai điểm M, N gọi là đối xứng nhau qua điểm I nếu …
A. I là trung điểm của đoạn MN
B. I là điểm nằm ngoài đoạn MN
C. I là điểm cách M một khoảng bằng 12
D. I là điểm chia đoạn MN thành tỉ số 2:3
Đáp án: A
Giải thích:
+ Theo định nghĩa hai điểm đối xứng qua một điểm: Ha điểm M, N gọi là đối xứng với nhau qua điểm I nếu I là trung điểm của đoạn thẳng MN nên A đúng.
Bài 11: Tam giác ABC đối xứng với tam giác A’B’C’ qua O. Biết chu vi của tam giác A’B’C’ là 32cm. Chu vi của tam giác ABC là:
A. 32dm
B. 64cm
C. 16cm
D. 32cm
Đáp án: D
Giải thích:
Vì tam giác ABC đối xứng với tam giác A’B’C’
qua O nên ΔABC = ΔA’B’C’
=> AB = A’B’; AC = A’C’; BC = B’C’
Nên AB + AC + BC = A’B’ + A’C’ + B’C’
=> PABC = PA’B’C’
Do đó chu vi tam giác ABC là PABC = 32cm
Bài 12: Cho tam giác ABC, trong đó AB = 15cm, BC = 12cm. Vẽ hình đối xứng với tam giác ABC qua trung điểm của cạnh AC. Chu vi của tứ giác tạo thành là:
A. 54cm
B. 53cm
C. 52cm
D. 51cm
Đáp án: A
Giải thích:
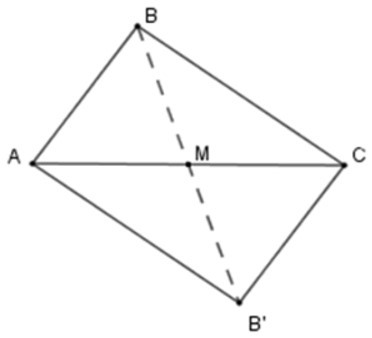
Lấy M là trung điểm AC khi đó A, C đối xứng nhau qua M. Vẽ B’ đối xứng với B qua O. Khi đó tam giác B’AC đối xứng với tam giác ABC qua M. Tứ giác tạo thành là ABCB’.
Vì tam giác B’AC đối xứng với tam giác BCA qua M
nên AB’ = BC = 15cm;
B’C = AB = 12cm
Chu vi tam giác ABCB’ là AB + AC + CB’ + AB’
= 12 + 15 + 12 + 15 = 54 cm
Bài 13: Cho tam giác ABC, đường cao AH, trong đó BC = 18cm, AH = 3cm. Vẽ hình đối xứng với tam giác ABC qua trung điểm của cạnh BC. Diện tích của tam giác tạo thành là:
A. 24cm2
B. 54cm2
C. 20cm2
D. 27cm2
Đáp án: D
Giải thích:
Gọi tam giác A’CB đối xứng với tam giác ABC qua trung điểm cạnh BC.
Khi đó ΔABC = ΔA’CB
Nên SABC = SA’BC.
Ta có SABC =12 AH.BC
= 12.3.18 = 27 cm2
nên SA’BC = 27cm2
Bài 14: Cho tam giác ABC. Gọi D là điểm đối xứng với B qua A, E là điểm đối xứng với C qua A. Lấy các điểm I, K theo thứ tự thuộc các đoạn thẳng DE, BC sao cho DI = BK. Chọn câu đúng.
A. ED // BC
B. Điểm I đối xứng với điểm A qua K
C. ΔAED = ΔABC
D. Cả A, B, C đều đúng
Đáp án: A
Giải thích:
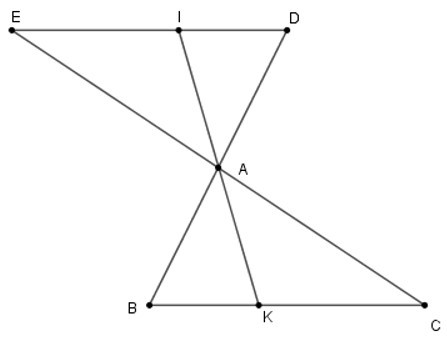
Xét ΔADE và ΔABC có:
+ AD = AB (vì D đối xứng với B qua A)
+ ^EAD =^BAC (đối đỉnh)
+ AE = AC (vì E đối xứng với C qua A)
Nên ΔADE = ΔABC (c – g – c),
suy ra ^EDA =^ABC mà hai góc này ở vị trí so le trong
nên ED // BC
Xét ΔADI và ΔABK có:
+ AD = AB (vì D đối xứng với B qua A)
+ ^EDA =^ABC (cmt)
+ DI = BK (gt)
Nên ΔADI = ΔABK (c – g – c)
=> ^IAD =^KAB mà B, A, D thẳng hang
Nên K, A, I thẳng hang
Lại có IA = AK (do ΔADI = ΔABK) nên điểm K đối xứng với I qua A.
Bài 15: Cho hình bình hành ABCD có tâm đối xứng là O, E là điểm bất kỳ trên đoạn OD. Gọi F là điểm đối xứng của C qua E.
1. Tứ giác ODFA là hình gì?
A. Hình thang
B. Hình bình hành
C. Hình thang cân
D. Hình thang vuông
Đáp án: A
Giải thích:
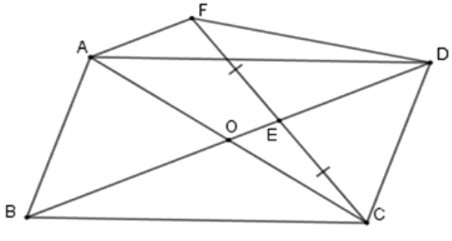
+ Xét tam giác CAF có E là trung điểm của CF (do F là điểm đối xứng của điểm C qua E); O là trung điểm AC (do O là tâm đối xứng của hình bình hành ABCD) nên OE là đường trung bình của tam giác CAF
=> OE =12 AF; OE // AF suy ra OD // AF
=> ODFA là hình thang.
2. Xác định vị trí điểm E trên OD để hình thang ODFA là hình bình hành.
A. E là chân đường vuông góc kẻ từ C đến OD
B. E là trung điểm của OD
C. Cả A, B đều sai
D. Cả A, B đều đúng
Đáp án: B
Giải thích:
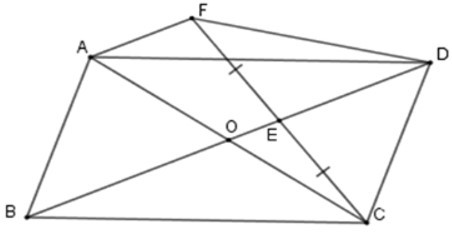
Để hình thang ODFA là hình bình hành thì ta cần OD = AF
mà OE =12 AF (cmt) nên OE = OD
Hay E là trung điểm của OD
Bài 16: Cho hình bình hành ABCD, O là giao điểm của hai đường chéo, Một đường thẳng đi qua O cắt các cạnh AB và CD theo thứ tự ở M và N. Chọn khẳng định đúng.
A. Điểm M đối xứng với điểm N qua O
B. Điểm M đối xứng với điểm O qua N
C. Điểm N đối xứng với điểm O qua M
D. Điểm A đối xứng với điểm B qua M
Đáp án: A
Giải thích:
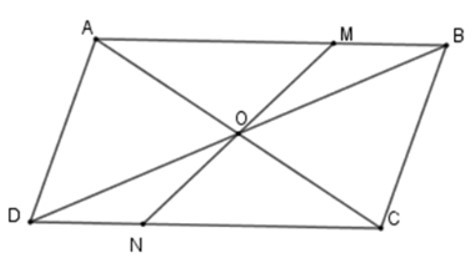

Suy ra điểm M đối xứng với điểm N qua O.
Bài 17: Chọn đáp án đúng trong các đáp án sau
A. Hai điểm được gọi là đối xứng với nhau qua điểm O nếu O thuộc đoạn nói hai điểm đó.
B. Hai điểm được gọi là đối xứng với nhau qua điểm O nếu O các đều hai điểm đó
C. Hai điểm được gọi là đối xứng với nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.
D. Hai điểm được gọi là đối xứng với nhau qua điểm O nếu O là đoạn thẳng trung trực của hai điểm đó.
Đáp án: C
Giải thích:
Hai điểm gọi là đối xứng với nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.
Bài 18: Cho AB = 6cm, A' là điểm đối xứng với A qua B, AA' có độ dài bằng bao nhiêu ?
A. AA' = 3cm
B. AA' = 12cm
C. AA' = 6cm
D. AA' = 9cm
Đáp án: B
Giải thích:
Định nghĩa: Hai điểm gọi là đối xứng với nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.
Khi đó, A' là điểm đối xứng với A qua B thì AB = BA' = 6cm
⇒ AA' = AB + BA' = 6 + 6 = 12cm
Bài 19: Chọn phương án sai trong các phương án sau đây
A. Hai đoạn thẳng đối xứng với nhau qua một điểm thì chúng bằng nhau.
B. Hai góc đối xứng với nhau qua một điểm thì chúng bằng nhau.
C. Hai đường thẳng đối xứng với nhau qua một điểm thì chúng bằng nhau.
D. Hai tam giác đối xứng với nhau qua một điểm thì chúng bằng nhau.
Đáp án: C
Giải thích:
Ta có tính chất: Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một điểm thì chúng bằng nhau.
Các phương án đúng là:
+ Đáp án A: Hai đoạn thẳng đối xứng với nhau qua một điểm thì chúng bằng nhau.
+ Đáp án B: Hai góc đối xứng với nhau qua một điểm thì chúng bằng nhau.
+ Đáp án D: Hai tam giác đối xứng với nhau qua một điểm thì chúng bằng nhau.
→ Đáp án C sai.
Bài 20: Hình nào dưới đây có tâm không phải là giao điểm của hai đường chéo?
A. Hình bình hành
B. Hình chữ nhật
C. Hình thoi
D. Hình thang
Đáp án: D
Giải thích:
Các hình có tâm đối xứng là giao điểm điểm của hai đường chéo là
+ Hình bình hành
+ Hình chữ nhật
+ Hình thoi
→ Hình thang không có tâm đối xứng là giao điểm của hai đường chéo.
Bài 21: Cho tam giác ABC và tam giác A'B'C' đối xứng với nhau qua điểm I biết AB = 4cm, AC = 8cm và chu vi của tam giác ABC bằng 22cm. Hỏi độ dài cạnh B'C' của tam giác A'B'C' là?
A. B'C' = 9cm
B. B'C' = 8cm
C. B'C' = 4cm
D. B'C' = 10cm
Đáp án: D
Giải thích:
Ta có tính chất: Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một điểm thì chúng bằng nhau.
Khi đó ta có:
⇒ BC = B'C' = 22 - 8 - 4 = 10( cm )
Bài 22: Có bao nhiêu câu đúng trong hình
a) Tâm đối xứng của một đường thẳng là điểm bất kì của đường thẳng đó.
b) Trọng tâm của một tam giác là tâm đối xứng của tam giác đó.
c) Hai tam giác đối xứng với nhau qua một điểm thì có chu vi bằng nhau.
A. 0
B. 1
C. 2
D. 3
Đáp án: C
Giải thích:
a) Đúng, vì nếu lấy một điểm O bất kì trên đường thẳng thì nó chia đường thẳng đó thành hai và với bất kì một điểm M, trên tia này cũng luôn có một điểm M’ đối xứng với nó qua O trên tia kia.
b) Sai,
Giả sử tam giác ABC có trọng tâm G.
Khi đó điểm A’ đối xứng với A qua G không nằm trong tam giác.
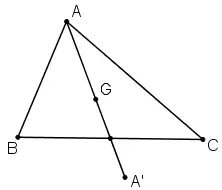
c) Đúng, vì hai tam giác đối xứng với nhau qua một điểm thì chúng bằng nhau.
Do đó chu vi của chúng bằng nhau.
Bài 23:
Trong các hình sau, có mấy hình có tâm đối xứng?
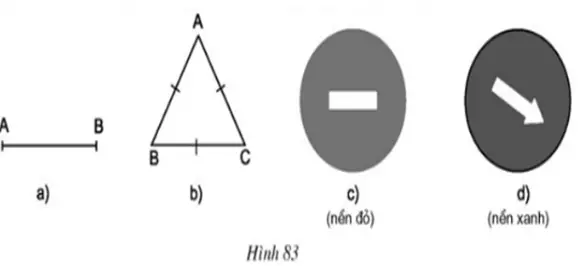
A. 2
B. 1
C. 3
D. 4
Đáp án: A
Giải thích:
– Hình 83a có tâm đối xứng là trung điểm của đoạn thẳng AB
– Hình 83b không có tâm đối xứng
(Lưu ý: Trọng tâm đồng thời là trực tâm của tam giác đều ABC không phải tâm đối xứng của tam giác đó)
– Hình 83c có tâm đối xứng là tâm của hình tròn.
– Hình 83d không có tâm đối xứng.
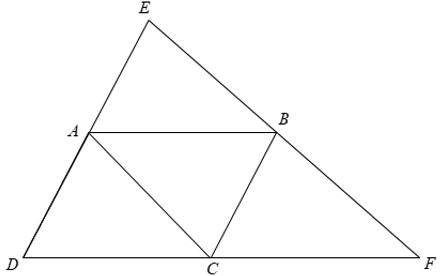
Bài 24: Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua A, F là điểm đối xứng với D qua C. Khẳng định nào sai?
A. AC // EF
B. Điểm E đối xứng với điểm F qua điểm B.
C. AB là đường trung bình của tam giác DEF
D. Điểm E đối xứng với điểm A qua điểm D.
Đáp án: D
Giải thích:
E là điểm đối xứng với D qua A ⇒ A là trung điểm của DE.
F là điểm đối xứng với D qua C ⇒ C là trung điểm của DF.
a) Xét Δ DEF có
⇒ AC là đường trung bình của Δ DEF.
⇒ AC // EF
+ AC là đường trung bình của tam giác Δ DEF
⇒ AC = 1/2EF
+ ABCD là hình bình hành
Mà DC = CF ⇒ AB = 1/2DF.
⇒ AB là đường trung bình của Δ DEF
Do đó B là trung điểm của EF hay E đối xứng với F qua B.
Bài 25: Hình nào dưới đây vừa có tâm đối xứng vừa có trục đối xứng?
A. hình bình hành
B. hình chữ nhật
C. hình tam giác đều
D. hình tam giác cân
Đáp án: B
Giải thích:
Hình bình hành có tâm đối xứng; hình tam giác cân và hình tam giác đều chỉ có trục đối xứng
Bài 26: Hình nào dưới đây không có tâm đối xứng?
A. Hình thoi
B. Hình bình hành
C. Hình thang cân
D. Hình chữ nhật
Đáp án: C
Giải thích:
- Hình chữ nhật có hai trục đối xứng là đường nối hai trung điểm của hai cạnh đối diện và tâm đối xứng là giao của hai đường chéo.
- Hình thang không có trục đối xứng, cũng ko có tâm đối xứng.
- Hình hình hành không có trục đối xứng và có tâm đối xứng là giao điểm của hai đường chéo.
- Hình thoi là hình có hai trục đối xứng là hai đường chéo và tâm đối xứng là giao điểm của hai đường chéo.
Các câu hỏi trắc nghiệm Toán lớp 8 có đáp án, chọn lọc khác:
Trắc nghiệm Hình chữ nhật có đáp án
Trắc nghiệm Đường thẳng song song với một đường thẳng cho trước có đáp án
Trắc nghiệm Hình thoi có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Sinh học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Toán lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Hóa học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn lớp 11 có đáp án
- Trắc nghiệm Tiếng Anh lớp 11 có đáp án
- Trắc nghiệm Vật Lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Địa lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm GDCD lớp 11 có đáp án
- Trắc nghiệm Lịch sử lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Công nghệ lớp 11 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 11 có đáp án
- Trắc nghiệm Tin học lớp 11 có đáp án
- Trắc nghiệm Toán lớp 12 có đáp án
- Trắc nghiệm Sinh học lớp 12 có đáp án
- Trắc nghiệm Hóa học lớp 12 có đáp án
- Trắc nghiệm Ngữ văn lớp 12 có đáp án
- Trắc nghiệm Tiếng Anh lớp 12 có đáp án
- Trắc nghiệm Địa lí lớp 12 có đáp án
- Trắc nghiệm Vật Lí lớp 12 có đáp án
- Trắc nghiệm Công nghệ lớp 12 có đáp án
- Trắc nghiệm Giáo dục công dân lớp 12 có đáp án
- Trắc nghiệm Lịch sử lớp 12 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 12 có đáp án