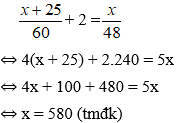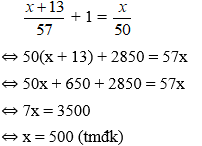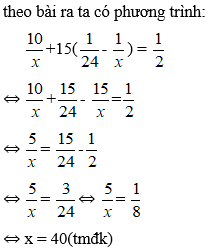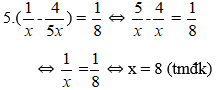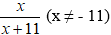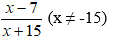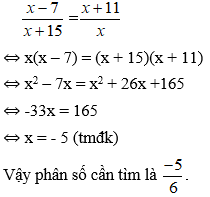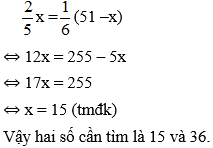Nội dung bài viết

    Xem thêm

    TOP 40 câu Trắc nghiệm Giải bài toán bằng cách lập phương trình (tiếp theo) (có đáp án 2023) - Toán 8

    Bộ 40 câu hỏi trắc nghiệm Toán lớp 8 Bài 7: Giải bài toán bằng cách lập phương trình (tiếp theo) có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 8 Bài 7.

    1 1,120 16/02/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Trắc nghiệm Toán 8 Bài 7: Giải bài toán bằng cách lập phương trình (tiếp theo)

    Bài giảng Trắc nghiệm Toán 8 Bài 7: Giải bài toán bằng cách lập phương trình (tiếp theo)

    Bài 1: Một xưởng dệt theo kế hoạch mỗi ngày phải dệt được 30 áo. Trong thực tế mỗi ngày xưởng dệt được 40 áo nên đã hoàn thành trước thời hạn 3 ngày, ngoài ra còn làm thêm được 20 chiếc áo nữa. Số sản phẩm thực tế làm được là:

    A. 420

    B. 440

    C. 500

    D. 450

    Đáp án: B

    Giải thích:

    Gọi số sản phẩm xưởng cần làm theo kế hoạch là:

     x (sản phẩm, x > 0, x ∈ N).

    Thời gian dự kiến xong là: x30 (ngày)

    Vì theo thực tế đội làm được thêm 20 sản phẩm nên số sản phẩm thực tế làm được là: x + 20 (sản phẩm).

    Thời gian làm thực tế là: x+2040 (ngày)

    Vì đội hoàn thành trước thời hạn 3 ngày nên

    ta có phương trình: x30-x+2040 -  = 3.

    ⇔4x120−3(x+20)120=3.120120

    ⇔ 4x – 3x – 60 =360

    ⇔ x = 420 (TM)

    Số sản phẩm theo dự kiến là: 420 (sản phẩm).

    Số sản phẩm làm được thực tế là:

     420 + 20 = 440 (sản phẩm).

    Bài 2: Một người đi xe máy từ A đến B, với vận tốc 30km/h. Lúc về người đó đi với vận tốc 24 km/h. Do đó thời gian về lâu hơn thời gian đi là 30 phút. Thời gian lúc đi là:

    A. 1 giờ

    B. 2 giờ

    C. 1,5 giờ

    D. 2,5 giờ

    Đáp án: B

    Giải thích:

    Đổi 30 phút = 3060=12 (h).

    Gọi thời gian lúc đi là x (giờ), quãng đường AB dài là: 30x (km)

    Thời gian người đó đi quãng đường AB lúc về là: 30x24 (h)

    Theo đề bài ta có phương trình 30x24-x=12

    ⇔30x24−24x24=1224

    ⇔ 30x – 24x = 12

    ⇔ 6x = 12

    ⇔ x = 2 (giờ)

    Bài 3: Một đội thợ mỏ theo kế hoạch mỗi ngày phải khai thác 50m3 than. Do siêng năng làm việc nên trên thực tế mỗi ngày đội khai thác được 57m3 than. Vì vậy không những đã xong trước thời hạn 1 ngày mà còn vượt mức 13m3 than. Theo kế hoạch, đội phải khai thác số m3 than là:

    A. 500m3

    B. 513m3

    C. 487m3

    D. 513m3

    Đáp án: A

    Giải thích:

    Gọi số ngày dự kiến đội hoàn thành khai thác theo kế hoạch là x (ngày, x > 0)

    Thời gian đội hoàn thành khai thác theo thực tế là: x – 1 (ngày)

    Lượng than đội dự kiến khai thác là: 50x(m3)

    Lượng than đội khai thác thực tế là 57(x – 1) (m3)

    Vì đội vượt mức 13m3 nên ta có phương trình:

    57(x – 1) = 50x + 13

    ⇔7x = 70

    ⇔ x = 10 (thỏa mãn)

    Vậy lượng than dự định khai thác là: 10.50 = 500 (m3)

    Bài 4: Một người đi xe máy từ A đến B với vận tốc 25 km/h. Lúc về người đó đi với vận tốc 30 km/h nên thời gian về ít hơn thời gian đi là 20 phút. Tính quãng đường AB?

    A. 40 km

    B. 70 km

    C. 50 km

    D. 60 km

    Đáp án: C

    Giải thích:

    Gọi quãng đường AB dài x (x > 0, km)

    Thời gian lúc đi là x25 (h)

    Thời gian lúc về là x30 (h)

    Vì thời gian về ít hơn thời gian đi là

    20 phút (=13 h) nên ta có phương trình

    x30+13=x25

    ⇔5x+50150=6x150

    ⇔5x + 50 = 6x

    ⇔x = 50 (TM)

    Vậy quãng đường AB dài 50km

    Bài 5: Một ca nô xuôi dòng từ A đến B hết 1h24 phút và ngược dòng hết 2h. Biết vận tốc dòng nước là 3km/h. Tính vận tốc riêng của ca nô?

    A. 16km/h

    B. 18km/h

    C. 17km/h

    D. 15km/h

    Đáp án: C

    Giải thích:

    Gọi vận tốc riêng của ca nô là x (x > 3) km/h

    Vận tốc khi xuôi dòng là x + 3 (km/h)

    Vận tốc khi ngược dòng là x – 3 (km/h)

    Đổi 1 giờ 24 phút = 75 giờ.

    Vì ca nô xuôi dòng và ngược dòng trên khúc sông AB nên ta có phương trình

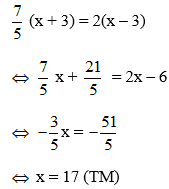
    Trắc nghiệm Giải bài toán bằng cách lập phương trình (tiếp theo) có đáp án - Toán lớp 8 (ảnh 1)

    Vậy vận tốc riêng của ca nô là 17 (km/h)

    Bài 6: Trong tháng Giêng hai tổ công nhân may được 800 chiếc áo. Tháng Hai, tổ 1 vượt mức 15%, tổ 2 vượt mức 20% do đó cả hai tổ sản xuất được 945 cái áo. Tính xem trong tháng đầu, tổ 1 may được bao nhiêu chiếc áo?

    A. 300

    B. 500

    C. 400

    D. 600

    Đáp án: A

    Giải thích:

    Gọi số áo tổ 1 làm được trong tháng Giêng là x (x ∈ N*; x < 800) (áo)

    Thì số áo tổ 2 làm được trong tháng Giêng là 800 – x (áo)

    Vì tháng Hai, tổ 1 vượt mức 15% nên số áo vượt mức là 15%.x =320 x (áo)

    Và tổ 2 vượt mức 20% nên số áo vượt mức là 20%(800 – x) =800-x5  (áo)

    Vì tháng Hai, cả hai tổ sản xuất được 945 cái áo nên vượt mức với tháng Giêng 945 – 800 = 145 áo

    Nên ta có phương trình

    320x + 800−x5 = 145

    ⇔ 3x + 3200 – 4x = 2900

    ⇔ x = 300 (TM)

    Vậy trong tháng Giêng tổ 1 làm được 300 áo.

    Bài 7: Hình chữ nhật có đường chéo 10cm. Chiều rộng kém chiều dài 2cm. Diện tích hình chữ nhật là:

    A. 24cm2

    B. 36cm2

    C. 48cm2

    D. 64cm2

    Đáp án: C

    Giải thích:

    Giả sử hình chữ nhật ABCD có chiều dài AB = x (cm), (x > 2)

    Chiều rộng BC là: x – 2 (cm)

    Độ dài đường chéo AC = 10cm, theo định lí Pitago ta có:

    x2 + (x – 2)2= 102

    ⇔ x2 + x2 – 4x + 4 = 100

    ⇔ 2x2 – 4x – 96 = 0

    ⇔ (x – 8)(x + 6) = 0

     ⇔x−8=0x+6=0

     ⇔x=8(TM)x=−6(l)  

    Do đó chiều dài hình chữ nhật là: 8(cm) và chiều rộng là 6(cm) nên diện tích hình chữ nhật đó là 8.6 = 48 (cm2)

    Bài 8: Tổng của chữ số hàng đơn vị và hai lần chữ số hàng chục của một số có hai chữ số là 10. Nếu đổi chỗ hai chữ số này cho nhau thì ta thu được số mới nhỏ hơn số cũ là 18 đơn vị. Tổng các chữ số đã cho là:

    A. 9

    B. 8

    C. 6

    D. 10

    Đáp án: C

    Giải thích:

    Gọi số đã cho là ab¯ (a, b  {0; 1; 2; …; 9}, a ≠ 0

    Tổng chữ số hàng đơn vị và hai lần chữ số hàng chục

    là 10 nên b + 2a = 10 hay b = 10 – 2a

    Nếu đổi chỗ hai chữ số cho nhau ta đươc số ba¯  

    Số mới nhỏ hơn số cũ 18 đơn vị nên ta có: ab¯-ba¯ = 18

    ⇔10a + b – (10b + a) = 18

    ⇔9a – 9b = 18

    Thay b = 10 – 2a vào phương trình trên ta được:

    9a – 9(10 – 2a) = 18

    ⇔ 9a – 90 + 18a = 18

    ⇔ 27a = 108

    ⇔  a = 4

    Suy ra b = 10 – 2.4 = 2

    nên a + b = 4 + 2 = 6

    Bài 9: Một ca nô xuôi dòng từ A đến B hết 1h20 phút và ngược dòng hết 2h. Biết vận tốc dòng nước là 3km/h. Tính vận tốc riêng của ca nô?

    A. 16km/h

    B. 18km/h

    C. 20km/h

    D. 15km/h

    Đáp án: D

    Giải thích:

    Gọi vận tốc riêng của ca nô là x (x > 3) km/h

    Vận tốc khi xuôi dòng là x + 3 (km/h)

    Vận tốc khi ngược dòng là x – 3 (km/h)

    Đổi 1 giờ 20 phút = 43 giờ. Vì ca nô xuôi dòng và ngược dòng trên khúc sông AB nên ta có phương trình

    43(x + 3) = 2(x – 3)

    ⇔43x + 4 = 2x – 6

    ⇔23x = 10

    ⇔ x = 15 (TM)

    Vậy vận tốc riêng của ca nô là 15 (km/h)

    Bài 10: Hai vòi nước cùng chảy vào một bể thì bể sẽ đầy trong 3 giờ 20 phút. Người ta cho vòi thứ nhất chảy trong 3 giờ, vòi thứ hai chảy trong 2 giờ thì cả hai vòi chảy được  bể. Thời gian vòi một chảy một mình đầy bể là:

    A. 10 giờ

    B. 6 giờ

    C. 8 giờ

    D. 5 giờ

    Đáp án: D

    Giải thích:

    Đổi 3 giờ 20 phút = 103 giờ.

    Gọi thời gian vòi một chảy một mình đầy bể là x (giờ),

    điều kiện x > 103 

    Coi bể đầy bằng 1 ta có:

    Một giờ hai vòi chảy được 1 : 103 = 310 (bể)

    Một giờ vòi 1 chảy được 1x (bể).

    Một giờ vòi 2 chảy được 310-1x -  (bể)

    Trong 3 giờ vòi 1 chảy được 3. 1x = 3x (bể)

    Trong 2 giờ vòi 2 chảy được 2.(310−1x) (bể)

    Vòi 1 chảy trong 3 giờ vòi hai chảy trong 2 giờ được:

    3x +2.(310−1x)

    Theo bài ra ta có phương trình:

    3x + 2.(310−1x) = 45 

    ⇔3x+35−2x=45

    ⇔1x=15

    ⇔x = 5

    Vậy nếu chảy một mình thì vòi 1 chảy trong 5 giờ đầy bể.

    Bài 11: Trong tháng Giêng hai tổ sản xuất được 720 chi tiết máy. Tháng Hai, tổ 1 vượt mức 15%, tổ hai vượt mức 12% nên sản xuất được 819 chi tiết máy. Tính xem trong tháng giêng, tổ 2 sản xuất được bao nhiêu chi tiết máy?

    A. 300

    B. 490

    C. 420

    D. 350

    Đáp án: A

    Giải thích:

    Gọi số chi tiết máy tổ 1 làm được trong tháng Giêng là x (x ∈ N*; x < 720) (chi tiết máy)

    Thì số chi tiết máy tổ 2 làm được trong tháng Giêng

    là: 720 – x (chi tiết máy)

    Vì tháng Hai, tổ 1 vượt mức 15% nên số chi tiết máy vượt mức

    là: 15%.x = x (chi tiết máy)

    Và tổ 2 vượt mức 12% nên số chi tiết máy vượt mức

    là 12%(720 – x) = 3(720−x)25 (chi tiết máy)

    Vì tháng hai, cả hai tổ sản xuất được 819 chi tiết máy nên vượt mức với tháng Giêng là: 819 – 720 = 99 (chi tiết máy).

    Nên ta có phương trình:

    320 + 3(720−x)25 = 99

     ⇔5.3x + 4.3(720 – x) = 99.100

     ⇔3x = 1260

    ⇔ x = 420 (TM)

    Vậy trong tháng Giêng tổ một làm được 420 chi tiết máy

    Tổ hai làm được 720 - 420 = 300 chi tiết máy.

    Bài 12: Năm nay tuổi mẹ gấp 3 lần tuổi Phương. Phương tính rằng 13 năm nữa thì tuổi mẹ chỉ còn gấp 2 lần tuổi Phương. Hỏi năm nay Phương bao nhiêu tuổi?

    A. 13 tuổi

    B. 14 tuổi

    C. 15 tuổi

    D. 16 tuổi

    Đáp án: A

    Giải thích:

    Gọi x là tuổi của Phương năm nay. Điều kiện: x nguyên dương.

    Tuổi của mẹ năm nay là 3x tuổi.

    13 năm nữa tuổi của Phương là: x + 13 (tuổi)

    13 năm nữa tuổi của mẹ Phương là: 3x + 13 (tuổi)

    13 năm nữa thì tuổi mẹ chỉ còn gấp 2 lần tuổi Phương nên ta có phương trình:

    3x + 13 = 2(x + 13)

    ⇔ 3x + 13 = 2x + 26

    ⇔ x = 13 (tm)

    Vậy Phương năm nay 13 tuổi

    Bài 13: Tìm số tự nhiên có bốn chữ số, biết rằng nếu viết thêm chữ số 1 vào đằng trước ta được số A có năm chữ số, nếu viết thêm chữ số 4 vào đằng sau ta được số B có năm chữ số, trong đó B gấp 4 lần A

    A. 6789

    B. 6666

    C. 6699

    D. 9999

    Đáp án: B

    Giải thích:

    Gọi số phải tìm là abcd¯ là x. Điều kiện x ∈ N; 1000 ≤ x ≤ 9999

    Viết thêm chữ số 1 vào đằng trước ta được

    A = 1abcd¯=10000+abcd¯=10000+x 

    Viết thêm chữ số 4 vào đằng sau ta được

    B = abcd4¯=10abcd¯+4=10x+4

    Theo đề bài B = 4A nên có phương trình

    10x + 4 = 4(10000 + x)

    Giải phương tình 10x + 4 = 40000 + 4x

    ⇔10x – 4x = 40000 – 4

    ⇔6x = 39996

    ⇔x = 6666

    Giá trị x = 6666 thỏa mãn các điều kiện nêu trên.

    Số phải tìm là 6666.

    Bài 14: Hai ô tô khởi hành cùng một lúc từ hai tỉnh A và B cách nhau 150km, đi ngược chiều và gặp nhau sau 2 giờ. Biết rằng nếu vận tốc của ô tô A tăng thêm 15 km/h thì bằng 2 lần vận tốc ô tô, vận tốc ô tô B là:

    A. 30 km/h

    B. 36 km/h

    C. 45 km/h

    D. 25 km/h

    Đáp án: A

    Giải thích:

    Gọi vận tốc xe A là x (km/h, x > 0)

    Vận tốc ô tô B là x+152 (km/h)

    Quãng đường xe A đi được trong 2 giờ là 2x (km)

    Quãng đường xe B đi được trong 2 giờ

    là: 2.x+152 = x + 15 (km)

    Do hai xe gặp nhau sau 2 giờ và quãng đường AB dài 150km nên ta có phương trình: 2x + x + 15 = 150

    ⇔ 3x = 135 ⇔ x = 45 (TM)

    Vậy vận tốc xe B là:  = 30 km/h

    Bài 15: Một tổ sản xuất theo kế hoạch mỗi ngày phải sản xuất 50 sản phẩm. Khi thực hiện tổ đã sản xuất được 57 sản phẩm một ngày. Do đó hoàn thành trước kế hoạch 1 ngày và còn vượt mức 13 sản phẩm. Hỏi theo kế hoạch tổ sản xuất bao nhiêu sản phẩm?

    A. 550

    B. 400

    C. 600

    D. 500

    Đáp án: D

    Giải thích:

    Gọi tổng sản phẩm tổ phải sản xuất theo kế hoạch là x (x > 0, x∈N) (sản phẩm)

    Thời gian theo kế hoạch là x50 (ngày)

    Theo thực tế số sản phẩm tổ đã làm là x + 13 (sản phẩm)

    Vì thực tế tổ hoàn thành trước 1 ngày nên ta có phương trình

    x+1357+1=x50

    ⇔50(x + 13) + 2850 = 57x

    ⇔ 7x = 3500

    ⇔ x = 500 (TM)

    Vậy tổng sản phẩm theo kế hoạch là 500 sản phẩm

    Bài 16: Một mảnh vườn hình chữ nhật có chu vi 56m. Nếu tăng chiều dài 4m và giảm chiều rộng 2m thì diện tích tăng 8m2. Chiều dài của hình chữ nhật là:

    A. 16m

    B. 18m

    C. 15m

    D. 32m

    Đáp án: A

    Giải thích:

    Nửa chu vi của hình chữ nhật ban đầu là: 56 : 2 = 28 (m)

    Gọi chiều dài hình chữ nhật ban đầu là x(m), (0 < x < 28)

    Suy ra chiều rộng hình chữ nhật ban đầu là: 28 – x (m)

    Diện tích hình chữ nhật ban đầu là:

    x(28 – x) = 28x – x2 (m2)

    Tăng chiều dài lên 4m thì chiều dài mới là: x + 4 (m)

    Giản chiều rộng 2m thì chiều rộng mới là:

    28 – x – 2 = 26 – x (m).

    Diện tích hình chữ nhật mới là:

    (x + 4)(26 – x) = 104 + 22x – x2 (m2)

    Theo đề bài ta có phương trình:

    28x – x2 + 8 = 104 + 22x – x2

    ⇔6x = 96 ⇔ x = 16 (TM)

    Vậy chiều dài hình chữ nhật là 16m.

    Bài 17: Một hình chữ nhật có chu vi 372 m nếu tăng chiều dài 21m và tăng chiều rộng 10m thì diện tích tăng 2862m2. Chiều dài của hình chữ nhật ban đầu là:

    A. 132m

    B. 124m

    C. 228m

    D. 114m

    Đáp án: D

    Giải thích:

    Nửa chu vi của hình chữ nhật ban đầu là:

    372 : 2 = 186 (m)

    Gọi chiều dài hình chữ nhật ban đầu là x(m), (0 < x < 186)

    Suy ra chiều rộng hình chữ nhật ban đầu là: 186 – x (m)

    Diện tích hình chữ nhật ban đầu là:

    x(186 – x) = 186x – x2 (m2)

    Tăng chiều dài lên 21m thì chiều dài mới là: x + 21 (m)

    Tăng chiều rộng lên 10m thì chiều rộng là:

    186 – x + 10 = 196 – x (m).

    Diện tích hình chữ nhật mới là:

    (x + 21)(196 – x)

    = 175x – x2 + 4116 (m2)

    Theo đề bài ta có phương trình:

    186x – x2 + 2862 = 175x – x2 + 4116

     ⇔11x = 1254 ⇔ x = 114 (TM)

    Vậy chiều dài hình chữ nhật là 114m.

    Bài 18: Một đội máy cày dự định cày 40 ha ruộng 1 ngày. Do sự cố gắng, đội đã cày được 52 ha mỗi ngày. Vì vậy, chẳng những đội đã hoàn thành sớm hơn 2 ngày mà còn cày vượt mức được 4 ha nữa. Tính diện tích ruộng đội phải cày theo dự định.

    A. 300 ha

    B. 630 ha

    C. 420 ha

    D. 360 ha

    Đáp án: D

    Giải thích:

    Gọi số ngày dự kiến đội hoàn thành cày ruộng theo kế hoạch là x (ngày, x > 0)

    Đội hoàn thành diện tích ruộng theo kế hoạch là: 40x (ha)

    Thời gian thực tế đội hoàn thành diện tích ruộng là: x – 2 (ngày)

    Đội hoàn thành diện tích ruộng theo thực tế là: 52(x – 2) (ha)

    Vì tổ vượt mức 4ha nên ta có phương trình:

    52(x – 2) = 40x + 4

    ⇔12x = 108 ⇔ x = 9 (thỏa mãn)

    Vậy diện tích ruộng cần cày theo dự định là 9.40 = 360 (ha)

    Bài 19: Lúc 7 giờ một người đi xe máy khởi hành từ A với vận tốc 30 km/h. Sau đó một giờ, người thứ hai cũng đi xe máy từ A đuổi theo với vận tốc 45 km/h. Hỏi đến mấy giờ người thứ hai mới đuổi kịp người thứ nhất?

    A. 7 giờ

    B. 8 giờ

    C. 10 giờ

    D. 9 giờ

    Đáp án: C

    Giải thích:

    Gọi thời gian người thứ nhất đi đến khi gặp nhau là x (x > 1) (giờ)

    Thì thời gian người thứ hai đi đến khi gặp nhau là x – 1 (giờ)

    Vì quãng đường hai người đi là bằng nhau nên ta có phương trình

    30x = 45(x – 1)

    ⇔ 15x = 45

    ⇔ x = 3 (TM)

    Vậy người thứ hai đuổi kịp người thứ nhất lúc 7 + 3 = 10 giờ

    Bài 20: Có 15 quyển vở gồm hai loại: loại I giá 2000 đồng một quyển, loại II giá 1500 đồng một quyển. Số tiền mua 15 quyển vở là 26000 đồng. Hỏi có mấy quyển vở loại I?

    A. 10 quyển vở

    B. 5 quyển vở

    C. 7 quyển vở

    D. 8 quyển vở

    Đáp án: C

    Giải thích:

    Gọi số vở loại I là x quyển (x ϵ N, 0 ≤ x ≤ 15) số vở loại II là 15 - x (quyển)

    Số tiền mua vở loại I là 2000x đồng, số tiền mua vở loại II là 1500(15 – x) đồng

    Tổng số tiền mua 15 quyển vở là 26000 đồng nên ta có phương trình:

    2000x + 1500(15 - x) = 26000

    ⇔ 2000x + 22500 – 1500x = 26000

    ⇔ 500x = 3500 ⇔ x = 7 (tmđk)

    Vậy có 7 quyển vở loại I và 15 – 7 = 8 quyển vở loại II

    Bài 21: Một xí nghiệp dự định mỗi ngày sản xuất 120 sản phẩm. Trong thực tế mỗi ngày xí nghiệp đã sản xuất được 130 sản phẩm nên đã hoàn thành kế hoạch sớm hơn 2 ngày . Hỏi xí nghiệp đã sản xuất được bao nhiêu sản phẩm ?

    A. 2610 sản phẩm

    B. 3000 sản phẩm

    C. 2600 sản phẩm

    D. 3120 sản phẩm

    Đáp án: D

    Giải thích:

    Gọi số ngày dự định làm theo kế hoạch là x ngày (x > 2)

    Số ngày thực tế làm là x – 2 (ngày)

    Số sản phẩm sản xuất theo dự định 120.x (sản phẩm), số sản phẩm sản suất theo thực tế 130(x – 2)(sản phẩm)

    Theo bài ra ta có phương trình:

    120x = 130.(x – 2)

    ⇔ 120x = 130x – 260

    ⇔ 10x = 260

    ⇔ x = 26 (tmđk)

    Vậy số sản phẩm xí nghiệp đã sản xuất được là 120.26 = 3120 sản phẩm.

    Bài 22: Một đội máy kéo dự định mỗi ngày cày được 40 ha. Khi thực hiện đội mỗi ngày cày được 52 ha . Vì vậy đội không những đã hoàn thành xong trước kế hoạch 2 ngày mà còn cày thêm được 4 ha nữa . Tính diện tích ruộng mà đội phải cày theo kế hoạch ?

    A. 360ha.

    B. 60ha.

    C. 120ha.

    D. 240ha.

    Đáp án: A

    Giải thích:

    Gọi thời gian dự định hoàn thành công việc là x (ngày) (x > 2)

    Diện tích ruộng mà đội phải cày theo kế hoạch là 40x (ha)

    Thời gian thực tế đội đã làm để hoàn thành công việc là x – 2 (ngày)

    Diện tích ruộng đội đã cày được theo thực tế là: 52(x – 2)

    Theo bài ra ta có phương trình:

    40x + 4 = 52(x – 2)

    ⇔ 40x + 4 = 52x – 104

    ⇔ 12x = 108

    ⇔ x = 9 (tmđk)

    Vậy diện tích ruộng đội phải cày theo kế hoạch là 40.9 = 360ha.

    Bài 23: Một đội sản xuất dự định mỗi ngày làm được 48 chi tiết máy. Khi thực hiện mỗi ngày đội làm được 60 chi tiết máy. Vì vậy đội không những đã hoàn thành xong trước kế hoạch 2 ngày mà còn làm thêm được 25 chi tiết máy . Tính số chi tiết máy mà đội phải sản xuất theo kế hoạch ?

    A. 480 chi tiết.

    B. 580 chi tiết.

    C. 400 chi tiết.

    D. 500 chi tiết.

    Đáp án: B

    Giải thích:

    Gọi số chi tiết máy mà đội phải sản xuất theo kế hoạch là x (x ∈ N, x > 0)

    Số chi tiết máy thực tế đội đã sản xuất được là x + 25

    Số ngày hoàn thành công việc theo kế hoạch là 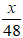Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán năng suất | Toán lớp 8 (ngày)

    Số ngày thực tế hoàn thành công việc là 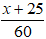Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán năng suất | Toán lớp 8 (ngày)

    Vì đội đã hoàn thành công việc xong trước 2 ngày so với kế hoạch nên ta có phương trình:

    Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán năng suất | Toán lớp 8

    Vậy số chi tiết máy đội phải sản xuất theo kế hoạch là 580 chi tiết.

    Bài 24: Một xí nghiệp dự định mỗi ngày sản xuất 50 sản phẩm. Trong thực tế mỗi ngày xí nghiệp đã sản xuất được 57 sản phẩm nên đã hoàn thành kế hoạch sớm hơn 1 ngày và sản xuất thêm được 13 sản phẩm. Hỏi theo kế hoạch xí nghiệp phải sản xuất được bao nhiêu sản phẩm ?

    A. 500 sản phẩm.

    B. 400 sản phẩm.

    C. 600 sản phẩm.

    D. 800 sản phẩm.

    Đáp án: A

    Giải thích:

    Gọi số sản phẩm xí nghiệp phải sản xuất theo kế hoạch là x (x ∈ N, x > 0)

    Số sản phẩm thực tế đội đã sản xuất được là x + 13 (sản phẩm)

    Số ngày dự định làm việc theo kế hoạch là 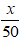Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán năng suất | Toán lớp 8 (ngày)

    Số ngày thực tế đội đã làm việc là 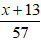Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán năng suất | Toán lớp 8 (ngày)

    Vì đội đã hoàn thành công việc xong trước 1 ngày so với kế hoạch nên ta có phương trình:

    Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán năng suất | Toán lớp 8

    Vậy số sản phẩm đội phải sản xuất theo kế hoạch là 500 sản phẩm.

    Đ/S: 500 sản phẩm.

    Bài 25: Một tổ sản xuất dự định mỗi ngày sản xuất 40 sản phẩm. Trong thực tế mỗi ngày tổ đã sản xuất được 45 sản phẩm. Do đó đã hoàn thành kế hoạch sớm hơn 2 ngày và sản xuất thêm được 5 sản phẩm. Hỏi theo kế hoạch tổ phải sản xuất được bao nhiêu sản phẩm ?

    A. 700 sản phẩm

    B. 760 sản phẩm

    C. 800 sản phẩm

    D. 560 sản phẩm

    Đáp án: B

    Giải thích:

    Gọi số ngày tổ sản xuất dự định làm theo kế hoạch là x ngày (x > 2)

    Số sản phẩm sản xuất theo kế hoạch là 40x

    Số ngày thực tế làm việc là x - 2(ngày)

    Số sản phẩm thực tế đã làm là 45(x – 2)

    Theo bài ra ta có phương trình:

    45(x – 2) = 40x + 5

    ⇔ 45x – 90 = 40x + 5

    ⇔ 5x = 95

    ⇔ x = 19 (tmđk)

    Vậy số sản phẩm tổ phải sản xuất theo kế hoạch là 40.19 = 760 sản phẩm

    Đ/S: 760 sản phẩm

    Bài 26: Hai đội công nhân cùng làm một công việc thì hoàn thành công việc đó trong 24 giờ. Nếu đội thứ nhất làm 10 giờ, đội thứ hai làm 15 giờ thì cả hai đội làm được một nửa công việc. Tính thời gian đội một làm một mình xong công việc.

    A. 40 giờ

    B. 20 giờ

    C. 30 giờ

    D. 10 giờ

    Đáp án: A

    Giải thích:

    Gọi thời gian để đội một làm một mình hoàn thành công việc là x giờ (x > 24)

    Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán năng suất | Toán lớp 8

    Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán năng suất | Toán lớp 8

    Vậy thời gian để đội một làm mình hoàn thành công việc là 40 giờ

    Bài 27: Một hợp tác xã dự định trung bình mỗi tuần đánh được 20 tấn cá. Nhưng do vượt mức 6 tấn/tuần nên chẳng những hoàn thành kế hoạch sớm hơn 1 tuần mà còn vượt mức 10 tấn. Tính sản lượng cá hợp tác xã dự định đánh bắt theo kế hoạch ?

    A. 100 tấn

    B. 240 tấn

    C. 360 tấn

    D. 120 tấn

    Đáp án: D

    Giải thích:

    Gọi thời gian dự định làm theo kế hoạch là x (tuần) (x > 1)

    Sản lượng cá dự tính đánh bắt được là 20x (tấn)

    Lượng cá thực tế đánh bắt được trong 1 tuần là 20 + 6 = 26 tấn.

    Thời gian thực tế hoàn thành công việc là x – 1 (tuần)

    Sản lượng cá thực tế đánh bắt được là 26(x – 1)

    Theo bài ra ta có phương trình:

    26(x – 1) = 20x + 10

    ⇔ 26x – 26 = 20x + 10

    ⇔ 6x = 36

    ⇔ x = 6 (tmđk)

    Vậy lượng cá phải đánh bắt theo kế hoạch là 20.6 = 120(tấn)

    Đ/S: 120 tấn

    Bài 28: Một tổ may áo sản xuất dự định mỗi ngày sản xuất 30 áo. Trong thực tế mỗi ngày tổ đã sản xuất được 40 chiếc áo. Do đó đã hoàn thành kế hoạch sớm hơn 3 ngày và sản xuất thêm được 20 chiếc áo. Hỏi theo kế hoạch tổ phải sản xuất được bao nhiêu chiếc áo ?

    A. 120 sản phẩm

    B. 300 sản phẩm

    C. 260 sản phẩm

    D. 420 sản phẩm

    Đáp án: D

    Giải thích:

    Gọi số áo tổ phải sản xuất theo kế hoạch là x áo (x ∈ N, x > 0)

    Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán năng suất | Toán lớp 8

    Vậy số áo mà tổ phải sản xuất theo kế hoạch là 420 áo

    Đ/S: 420 chiếc áo.

    Bài 29: Tổ Hùng được giao dệt một số thảm trong 20 ngày. Nhưng do tổ tăng năng suất 20% nên đã hoàn thành sau 18 ngày. Không những vậy mà tổ bạn Hùng còn làm thêm được 24 chiếc thảm. Tính số thảm thực tế tổ bạn Hùng làm được ?

    A. 324 sản phẩm.

    B. 300 sản phẩm.

    C. 648 sản phẩm.

    D. 200 sản phẩm.

    Đáp án: A

    Giải thích:

    Gọi số thảm mà tổ bạn Hùng được giao dệt trong một ngày là x thảm (x ∈ N, x > 0)

    Số thảm thực tế làm được trong một ngày là x + x.20% = 1,2x (thảm)

    Số thảm phải dệt theo kế hoạch là x.20 = 20x (thảm)

    Số thảm thực tế làm được là 18.1,2x = 21,6x (thảm)

    Do số thảm thực tế nhiều hơn số thảm phải làm theo kế hoạch 24 chiếc nên ta có phương trình:

    21,6x = 20x + 24 ⇔ 1,6x = 24 ⇔ x = 15 (tm đk)

    Vậy số thảm thực tế tổ bạn Hùng đã làm được là 15.21,6 = 324 chiếc thảm

    Đ/S: 324 sản phẩm.

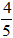
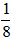
    Bài 30: Một vòi nước chảy vào một bể không có nước. Cùng lúc đó một vòi khác chảy từ bể ra. Mỗi giờ lượng nước chảy ra bằng Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán năng suất | Toán lớp 8 lượng nước chảy vào. Sau 5 giờ nước trong bể đạt tới Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán năng suất | Toán lớp 8 dung tích bể. Hỏi nếu bể không có nước mà chỉ mở vòi chảy vào bể thì sau bao lâu bể sẽ đầy nước?

    A. 6 giờ.

    B. 8 giờ.

    C. 9 giờ.

    D. 5 giờ.

    Đáp án: A

    Giải thích:

    Gọi thời gian để vòi chảy vào đầy bể nước là x (giờ) (x > 0)

    Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán năng suất | Toán lớp 8

    Sau 5 giờ lượng nước còn lại trong bể là 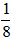Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán năng suất | Toán lớp 8 dung tích bể nên ta có phương trình:

    Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán năng suất | Toán lớp 8

    Vậy thời gian để bể đầy nước nếu chỉ mở vòi chảy là 8 giờ.

    Bài 31: Một số tự nhiên có hai chữ số có tổng các chữ số bằng 7. Nếu thêm chữ số 0 vào giữa hai chữ số ta được một số có 3 chữ số lớn hơn số đã cho là 180. Tìm số đó.

    A. 70

    B. 75

    C. 20

    D. 25

    Đáp án: D

    Giải thích:

    Gọi số tự nhiên có hai chữ số cần tìm là 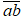Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán tìm số tự nhiên | Toán lớp 8 = 10a + b (a, b ∈ N,0 < a ≤ 7, 0 ≤ b < 7)

    Ta có a + b = 7 .

    Khi thêm chữ số 0 vào giữa ta được số 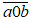Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán tìm số tự nhiên | Toán lớp 8 = 100a + b

    Vì số mới hơn số đã cho 180 nên ta có phương trình:

    100a + b = 10a + b + 180

    ⇔ 90a = 180

    ⇔ a = 2 (tmđk)

    ⇒ b = 7- a = 5

    Vậy số tự nhiên có hai chữ số cần tìm là 25.

    Bài 32: Hiệu của hai số bằng 50. Số này gấp ba lần số kia. Tìm hai số đó.

    A. 25

    B. 75

    C. 20

    D. 70

    Đáp án: B

    Giải thích:

    Gọi số nhỏ là x (x > 0), số lớn là 3x

    Vì hiệu hai số là 50 nên ta có phương trình:

    3x – x = 50 ⇔ 2x = 50 ⇔ x = 25 (tmđk)

    Vậy hai số cần tìm là 25 và 25.3 = 75

    Bài 33: Một số có 2 chữ số. Biết rằng chữ số hàng đơn vị gấp 3 lần chữ số hàng chục. Nếu đổi chỗ 2 chữ số cho nhau được số mới lớn hơn số cũ 54 đơn vị. Tìm số ban đầu ?

    A. 39

    B. 26

    C. 13

    D. 93

    Đáp án: A

    Giải thích:

    Gọi số cần tìm là 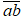Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán tìm số tự nhiên | Toán lớp 8 = 10a + b (a, b ∈ N. 0 < a < b < 10)

    Ta có b = 3a

    Khi đổi hai chữ số ta được số 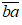Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán tìm số tự nhiên | Toán lớp 8 = 10b + a

    Vì số mới lớn hơn số cũ 54 đơn vị nên ta có phương trình: 10b + a – 54 = 10a + b

    ⇔ 9b – 9a = 54

    ⇔ 9.3a – 9a = 54

    ⇔ 18a = 54

    ⇔ a =3 (tmđk)

    Vậy số ban đầu cần tìm là 39.

    Bài 34: Tìm một số có hai chữ số biết rằng nếu viết thêm 5 vào bên phải số đó ta được số gấp 9 lần số đã cho khi cộng thêm 3.

    A. 22

    B. 27

    C. 32

    D. 17

    Đáp án: A

    Giải thích:

    Gọi số cần tìm là x (x∈ N, 10 ≤ x ≤ 99)

    Khi viết thêm 5 vào bên phải số đó ta được số mới là số có 3 chữ số với chữ số hàng đơn vị là chữ số 5. Khi đó số đã cho là số chục và số mới được viết là: 10x + 5.

    Số ban đầu khi cộng thêm 3 là: x + 3

    Theo bài ra ta có phương trình:

    10x + 5 = 9(x + 3)

    ⇔ 10x + 5 = 9x + 27

    ⇔ x = 22

    Vậy số cần tìm là số 22.

    Bài 35: Tìm số tự nhiên có bốn chữ số biết rằng nếu viết thêm một chữ số 1 vào đằng trước và một chữ số 1 vào đằng sau số đó thì số đó tăng gấp 21 lần

    A. 9099

    B. 9190

    C. 9091

    D. 9109

    Đáp án: C

    Giải thích:

    Gọi số có 4 chữ số cần tìm là x (x ∈ N, 1000 ≤ x ≤ 9999)

    Khi viết thêm 1 vào đằng trước và đằng sau số đã cho ta được số có sáu chữ số với chữ số hàng trăm nghìn và chữ số hàng đơn vị đều là chữ số 1. Số mới được viết là: 100000 + 10x + 1

    Vì số mới gấp 21 lần số cũ nên ta có phương trình: 100000 + 10x + 1 = 21x

    ⇔ 11x = 100001 ⇔ x = 9091(tmđk)

    Vậy số cần tìm là 9091

    Bài 36: Một phân số có tử số bé hơn mẫu số là 11, nếu bớt tử số đi 7 đơn vị, tăng mẫu số lên 4 đơn vị thì sẽ được phân số nghịch đảo của phân số đã cho. Tìm phân số ban đầu?

    A. 5/16

    B. - 5/6

    C. 8/19

    D. 1/12

    Đáp án: A

    Giải thích:

    Gọi tử số của phân số cần tìm là x (x ϵ Z)

    Mẫu số của phân số đó là x + 11

    Ta được phân số: Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán tìm số tự nhiên | Toán lớp 8

    Khi giảm tử số đi 7 đơn vị ta được x – 7, tăng mẫu lên 4 đơn vị thì mẫu mới là x + 15

    được phân số mới là Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán tìm số tự nhiên | Toán lớp 8

    phân số mới là nghịch đảo của phân số ban đầu nên ta có:

    Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán tìm số tự nhiên | Toán lớp 8

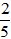
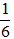
    Bài 37: Tổng của hai số bằng 51. Tìm hai số đó biết rằng Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán tìm số tự nhiên | Toán lớp 8 số thứ nhất bằng Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán tìm số tự nhiên | Toán lớp 8 số thứ hai.

    A. 15 và 36

    B. 16 và 35

    C. 21 và 30

    D. 24 và 27

    Đáp án: A

    Giải thích:

    Gọi số thứ nhất là x (x < 51)

    Số thứ hai là 51 – x

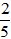
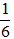
    Theo điều kiện đề bài Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán tìm số tự nhiên | Toán lớp 8 số thứ nhất bằng Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán tìm số tự nhiên | Toán lớp 8 số thứ hai nên ta có phương trình:

    Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán tìm số tự nhiên | Toán lớp 8

    Bài 38: Tìm hai số chẵn nguyên dương liên tiếp, biết tổng bình phương của chúng bằng 244.

    A. 10 và 12

    B. 14 và 12

    C. 14 và 16

    D. 20 và 22

    Đáp án: A

    Giải thích:

    Gọi số bé là x (x ∈ N*, x = 2k), số lớn là x + 2.

    Tổng bình phương của chúng là 244 nên ta có phương trình:

    x2 + (x + 2)2 = 244 ⇔ 2x2 + 4x + 4 = 244

    ⇔ x2 + 2x + 2 = 122 ⇔ x2 + 2x + 1 + 1 = 122

    ⇔ (x + 1)2 = 121 ⇔ (x + 1)2 = 112

    ⇔ x + 1 = 11 ⇔ x = 10 (tm đk)

    Vậy hai số cần tìm là 10 và 12.

    Bài 39: Tìm hai số lẻ nguyên dương liên tiếp, biết tổng bình phương của chúng bằng 514.

    A. 21 và 23.

    B. 13 và 15.

    C. 15 và 17.

    D. 17 và 19.

    Đáp án: C

    Giải thích:

    Gọi số bé là x (x ∈ N*, x = 2k + 1), số lớn là x + 2.

    Tổng bình phương của chúng là 514 nên ta có phương trình:

    x2 + (x + 2)2 = 514

    ⇔ 2x2 + 4x + 4 = 514

    ⇔ x2 + 2x + 2 = 257

    ⇔ x2 + 2x + 1 + 1 = 257

    ⇔ (x + 1)2 = 256

    ⇔ (x + 1)2 = 162

    ⇔ x + 1 = 16

    ⇔ x = 15 (tm đk)

    Vậy hai số cần tìm là 15 và 17.

    Bài 40: Cho hai số tự nhiên, biết thương của hai số là 3. Nếu thêm 10 vào số bị chia và giảm số chia đi một nửa thì hiệu của hai số mới là 30. Tìm số bị chia.

    A. 18

    B. 6

    C. 24

    D. 8

    Đáp án: C

    Giải thích:

    Gọi số chia ban đầu là x (x > 0)

    Số bị chia là 3x

    Khi thêm 10 vào số bị chia ta được số bị chia mới là 3x + 10, và giảm số chia đi một nửa thì số chia mới là Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán tìm số tự nhiên | Toán lớp 8

    Hiệu của hai số mới là 30 nên ta có phương trình:

    3x + 10 - 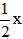Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán tìm số tự nhiên | Toán lớp 8 = 30

    ⇔ 6x + 20 – x = 60

    ⇔ 5x = 40 ⇔ x = 8 (tm đk)

    Vậy số chia ban đầu là 8 và số bị chia là 24.

    Các câu hỏi trắc nghiệm Toán lớp 8 có đáp án, chọn lọc khác:

    Trắc nghiệm Bài ôn tập Chương 3 có đáp án

    Trắc nghiệm Liên hệ giữa thứ tự và phép cộng có đáp án

    Trắc nghiệm Liên hệ giữa thứ tự và phép nhân có đáp án

    Trắc nghiệm Bất phương trình một ẩn có đáp án

    Trắc nghiệm Bất phương trình bậc nhất một ẩn có đáp án

    Tham khảo các loạt bài Trắc nghiệm lớp 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,120 16/02/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: